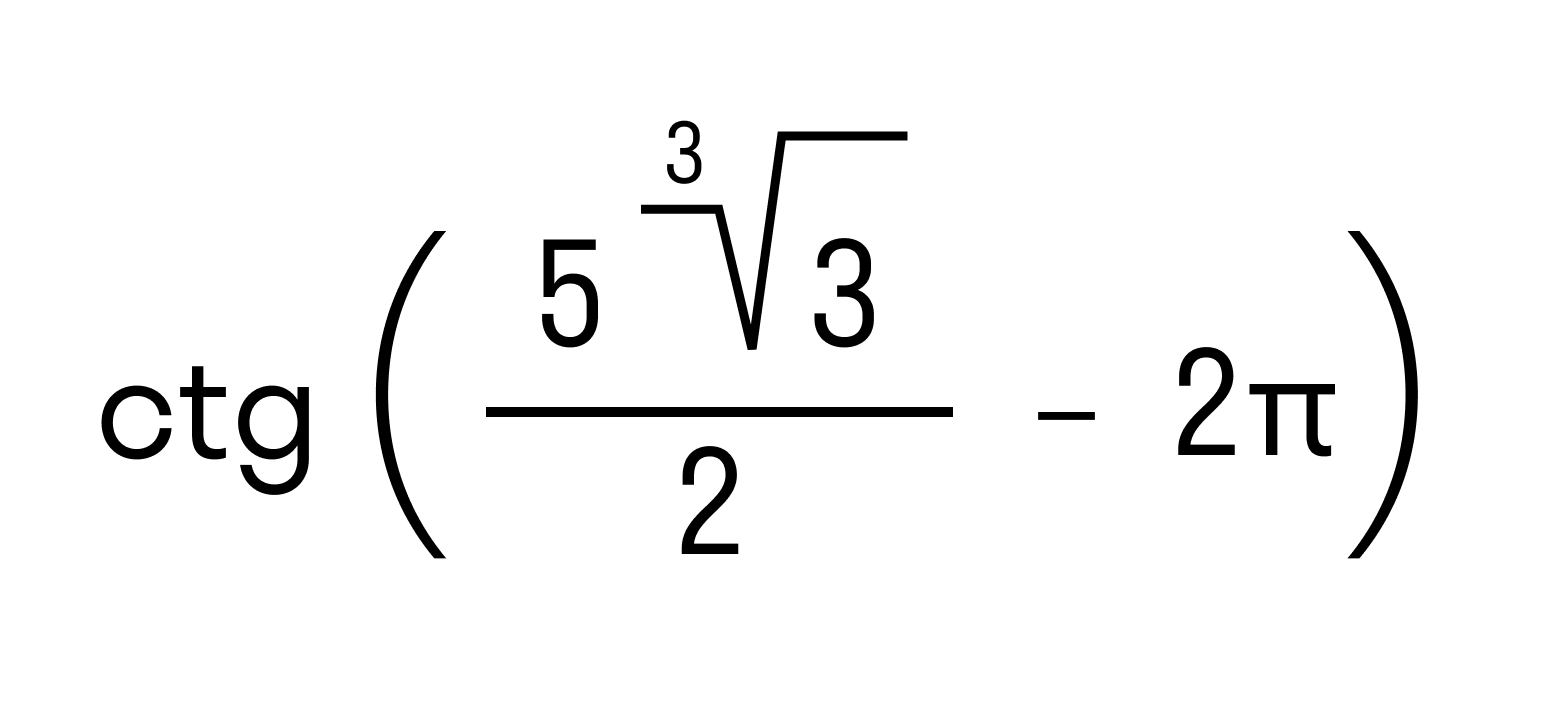поле действительных чисел это

Действительные числа

Действительные числа (вещественные числа) в их совокупности — это математический объект, представляющий собой классический одномерный континуум; каждое же отдельное вещественное число точно и строго выражает произвольную конечную и конечно малую величину на одном линейном протяжении («измерении»), либо отрицание этой величины.

На уровне аксиоматических определений, вещественные это расширение поля рациональных чисел, их пополнение — такое, что каждой точке прямой с отмеченной точкой (нулём) и заданной мерой протяжённости (единичным отрезком) соответствует некоторое допустимое значение: умножая единицу на это значение, мы получаем меру длины отрезка от нуля до данной точки.

где b — натуральное число или ноль (может принимать любое значение из множества [math]\mathbb N[/math] ∪ <0>); b₁, b₂, … — натуральные числа из множества <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>, то есть, арабские цифры и ноль.
При этом положительным числам r соответствует знак «+» слева (обычно опускается), отрицательным — знак «−».

Вещественные числа линейно (притом не вполне), упорядоченны: любые два разных вещественных числа можно сравнить. В частности, позиционная запись позволяет это сравнение проводить итеративно, сопоставляя каждый разряд, покуда не найдём разницу.

Вещественные числа образуют поле, множество вещественных чисел имеет мощность континуум (оно несчетно, и их нельзя поставить во взаимно-однозначное соответствие со множеством натуральных чисел, то есть «перенумеровать»). В современной математике вещественные числа определяются как полное упорядоченное поле или как пополнение поля рациональных чисел по стандартной метрике.

Содержание

[править] Рациональные и иррациональные числа

Поле вещественных чисел можно представлять себе как непересекающееся объединение рациональных и иррациональных чисел. Таким образом, иррациональные числа — вещественные числа, не являющиеся рациональными (не представимые в виде отношения целых чисел).

Любое рациональное число с помощью алгоритма Евклида может быть единственным образом представлено в виде (конечной) цепной дроби:
[math]\frac = a_0 + \cfrac<1>< \ddots + \cfrac<1> >>>[/math]
(a₀ — целое число, a_i — натуральные при 1 ≤ i ≤ k, и обычно полагается, что последний элемент a_k > 1, если рациональное число m/n — не целое).

[править] Аксиоматическое определение

Вещественные числа можно определить аксиоматически. Записанные в сокращенном виде аксиомы вещественных чисел выглядят так.

В Древней Греции было обнаружено, что рациональных чисел недостаточно для отображения точек числовой прямой, поскольку корень из 2 (длина диагонали квадрата со стороной 1) является иррациональным числом, не представимым в виде отношения целых чисел m/n. В дальнейшем появилось понимание, что вещественное число можно представлять себе как отношение, например отношение длины выбранного отрезка к заданному эталону. Это определение вещественного числа встречается у Ньютона. Современные более строгие концепции вещественных чисел появились в трудах Больцано, Вейерштрасса, Дедекинда и Кантора.

Поле вещественных чисел лежит в основе математического анализа.

[править] Обобщения

В алгебре и анализе вводятся комплексные числа — числа, представляющих собой сумму вещественного и мнимого числа (вещественное число, умноженное на абстрактную величину «корень из −1», обозначаемую буквой i). В рамках нестандартного анализа к вещественным числам добавляют бесконечно малые и бесконечно большие числа разных порядков. Рассматривается также алгебра кватернионов и др. обобщения.

Рациональные числа можно расширить не только до поля вещественных чисел, но и до поля p-адических чисел, если использовать другую метрику, связанную с делимостью на заданное простое число p (у «маленьких чисел» числитель дроби в несократимом представлении делится на «большую» степень простого числа p) и рассмотреть пополнение рациональных чисел по этой метрике. На базе p-адических чисел удается построить аналоги многих конструкций из математического анализа, созданных для вещественных чисел.

Источник

Действительные числа

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

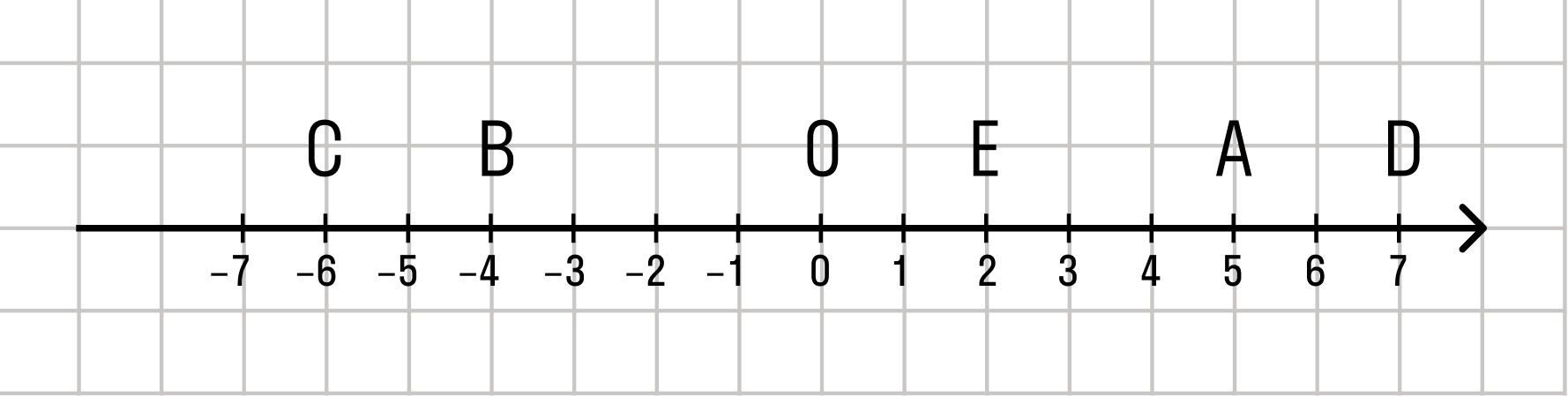
Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

О том, как правильно понимать определитель матрицы

Расшифровывается это дело следующим образом: если у нас есть матрица

над некоторым полем , то определителем этой матрицы называют сумму всевозможных произведений, состоящих изэлементов этой матрицы, взятых по одному из каждой строки и из каждого столбца, причем каждое произведение входит в эту сумму с тем знаком, который имеет соответствующая перестановка индексов этих элементов в этом произведении.

Другой способ введения определителя связан с его характеристическим свойством. Напомним, полилинейной формой называется функция , определенная на декартовом произведении некоторых векторных пространств (заданных над одним и тем же полем), принимающая значения в поле и линейная по каждому аргументу: . Форма называется кососимметрической, если при инверсии любых двух (не обязательно соседних) аргументов она меняет знак.

Можно конечно всюду далее рассматривать исключительно поля характеристики 2 и пользоваться «слабым» определением кососимметричности, а можно поступить умнее и немного усилить определение кососимметричности специально для полей характеристики 2 так, чтобы обычная кососимметричность следовала из «сильной». Для этого достаточно потребовать 2 вещи: во-первых, форма должна быть полилинейна, а во-вторых она должна принимать значение ноль всегда, когда среди ее аргументов есть равные. Свойство, которое вытекало из «наивной» кососимметричности для полей характеристики 2 само теперь является составной частью определения кососимметричности (правда только для полей характеристики 2).

Из полилинейности и равенства формы нулю на строках с равными аргументами следует, что если к одному вектору прибавить другой, умноженный на число, то значение формы не изменится. При умножении какого-либо вектора на число 0 сама форма умножается на это число (в частности, если обратить знак какого-либо вектора из набора, то знак самой формы тоже поменяется.

Произвести инверсию векторов в наборе аргументов можно с помощью преобразований этих двух типов. И если внимательно проследить цепочку преобразований, то в конце концов окажется, что форма поменяла знак.

Далее под кососимметричностью будем понимать кососимметричность в «сильном» смысле.

Определение

Определитель матриц— это единственная кососимметрическая полилинейная форма строк матрицы, нормированная единицей на единичном наборе векторов.

Надо сказать, это не самое плохое определение. Но и оно не лишено недостатков. Основные вопросы здесь возникают по поводу кососимметричности. В первую очередь непонятно, почему это свойство вообще важно. Ну меняет функция знак при перестановке двух аргументов и пусть меняет, почему мы так стремимся исследовать именно это свойство, а не какое-нибудь другое. Но здесь все еще хуже. Мы хотим, чтобы форма еще и принимала нулевое значение на наборе, содержащем равные вектора. И в некотором смысле для нас это даже важнее самой кососимметричности, раз мы стали подгонять определение последней под выполнение этого свойства. Все эти экзерсизы с характеристиками выглядят довольно искусственно.

В действительности есть очень простой и естественный пусть построения определителя, при котором все эти вопросы отпадают сами собой. И я постараюсь по возможности максимально последовательно описать этот способ.

Начнем с некоторых предварительных замечаний. Основным объектом изучения линейной алгебры являются конечномерные векторные пространства. Неформально говоря, на любое — мерное векторное пространство над полемможно смотреть как на «координатное» пространство, состоящее из упорядоченных наборов длины элементов поля. Более строго, пусть у нас есть— мерное векторное пространство над полем . Выбор (упорядоченного) базиса этого пространства индуцирует изоморфизм , ставящий в соответствие каждому вектору набор его координат в базисе . Таким образом, во всех дальнейших построениях речь пойдет по большей части про вектора координатного пространства.

Очевидно, некоторый набор векторов пространства является линейно (не)зависимым, тогда и только тогда, когда соответствующий ему набор векторов пространства будет линейно (не)зависимым.

Свойство линейной зависимости/независимости действительно очень важно. Дело в том, что система из 1″ alt=»n>1″ src=»https://habrastorage.org/getpro/habr/upload_files/4e1/89f/e1d/4e189fe1dc9b6260122146ddfd0031b7.svg»/>векторов пространства будет линейно зависимой тогда и только тогда, когда найдется вектор в этой системе, который можно линейно выразить через остальные.

Довольно естественным выглядит желание иметь некоторую функцию— индикатор линейной зависимости векторов. Учитывая, что любое векторное пространство «оцифровывается» своим координатным пространством, достаточно иметь такую функцию, определенную на декартовом произведениикопий пространстваи принимающую значения в поле. Таким образом, мы предъявляем к функциивсего лишь 2 очень естественных требования:

Она должна принимать нулевое значение на любой линейно зависимой системе векторов.

На аргументы этой функции удобно смотреть как на строки матрицы

Заметим, на данном этапе мы еще даже не знаем, существует ли такая функция или нет. Но мы можем в предположении ее существования посмотреть на ее поведение.

. Действительно, строка аргументов, содержащая пару равных значений, очевидно, линейно зависима, а значит функциябудет принимать на ней нулевое значение.

кососимметрична (в любом смысле, учитывая полилинейность + п.1). Доказательство абсолютно аналогично тому, которое находится выше под спойлером.

Рассмотрим, чему равнана некотором наборе строк :

Здесь мы просто выразили векторы через единичные, затем по полилинейности получили сумму по всем упорядоченным наборам соответствующих произведений, выкинули из них те, которые содержат повторяющиеся аргументы (тем самым получив сумму по всем перестановкам), а затем применили обратные перестановки к единичным векторам.

Смотрим на последнюю строчку в получившейся формуле и видим множитель . Чтобы упростить формулу и не таскать лишний множитель, добавим к тем 2 требованиям к функциитретье требование: .

Таким образом, если интересующая нас функциясуществует, то она имеет вид:

Нарисовалась знакомая нам формула Лейбница. Самое замечательное то, что в ней нет свободных переменных, а это значит, что мы бесплатно получили единственность интересующей нас функции.

Осталось лишь доказать существование. Капитан намекает, что для этого достаточно взять ту функцию, которая у нас получилась.

А дальше дело техники. Проверяем, что получили мы действительно, что хотели и даже больше. Полученную функцию называем определителем и спокойно приступаем к доказательству основных его свойств.

Источник