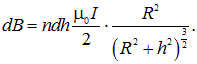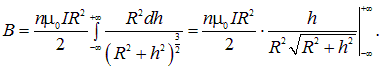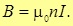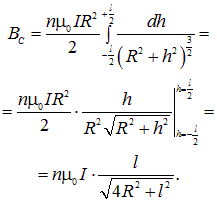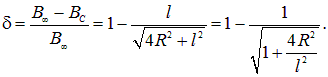поле бесконечно длинного соленоида

Поле бесконечно длинного соленоида

Применим теорему о циркуляции вектора для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).

Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.

Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.

Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.

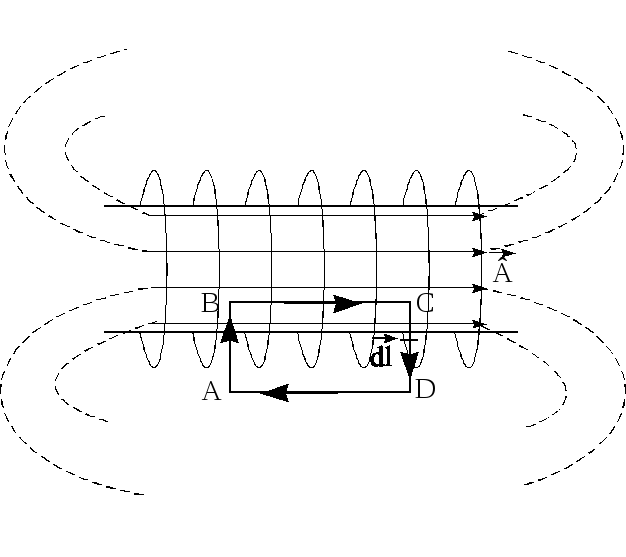
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.

Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е .

Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда

где – магнитная индукция на участке 1–2 – внутри соленоида, – магнитная проницаемость вещества.

Если отрезок 1–2 внутри соленоида, контур охватывает ток:

где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).

Тогда магнитная индукция внутри соленоида:

,

(2.7.1)

и , т.е. .

Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.

Произведение nI – называется число ампер витков на метр.

У конца полубесконечного соленоида, на его оси магнитная индукция равна:

,

(2.7.2)

Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.

Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:

· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:

,

(2.7.3)

где L – длина соленоида, R – радиус витков.

· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле

,

(2.7.4)

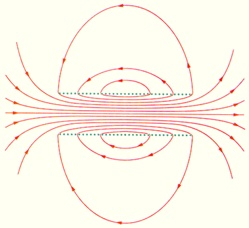
На рисунке 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.

Источник

Магнитное поле бесконечно длинного соленоида

Подставим эти проекции вектора Вв уравнение (6.12). Получим

Из этого равенства вытекает, что внутри соленоида вектор магнитной индукции не только сохраняет свое направление, но его модуль здесь всюду одинаков. Таким образом, приходим к выводу, что внутри длин­ного соленоида магнитное поле является однородным.

Рис. 6.6. Магнитное поле соленоида

Найдем модуль вектора магнитной индукции поля внутри соленоида при помощи теоремы (6.8) о циркуляции этого вектора. В качестве кон­тура С, по которому будем вычислять циркуляцию вектора магнитной индукции, выберем ломанную линию, изображенную пунктиром на рис. 6.6. Отрезок этой линии длиной l находится внутри соленоида и совпа­дает с одной из силовых линий магнитного поля. Две перпендикулярные этому отрезку прямые начинаются на его концах и уходят в бесконеч­ность. Во всех точках этих прямых вектор магнитной индукции или перпендикулярен им (внутри соленоида), или равен нулю (вне соленои­да). Поэтому скалярное произведение Вdlв этих точках равно нулю. Таким образом, циркуляция магнитной индукции по рассматриваемому контуру С будет равна интегралу по отрезку силовой линии длиной l. С учетом того, что модуль вектора магнитной индукции есть постоянная величина будем иметь

= =B =B l

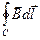
из которого найдем магнитную индукцию поля в соленоиде:

n-число витков, приходящихся на единицу длины соленоида.

Магнитное поле прямого тока

Рассмотрим магнитное поле, создаваемое электрическим током, теку­щим по тонкому бесконечно длинному проводу. Такая система обладает цилиндрической симметрией. Вследствие этого магнитное поле должно обладать следующими свойствами:

1) на любой прямой, параллельной проводу с током, вектор магнитной индукции должен быть всюду оди­наков;

2) при повороте всего магнитного поля целиком вокруг провода оно не изменяется. В таком случае силовыми линиями магнитного поля должны быть окружности, центры которых лежат на оси провода с то­ком (рис, 6.7), а вектор В на любой из этих окружностей всюду имеет один и тот же модуль.

При помощи теоремы (6.8) о циркуляции вектора магнитной индук­ции найдем модуль этого вектора. С этой целью вычислим циркуляцию магнитной индукции по одной из силовых линий С, радиус которой ра­вен а. Так как вектор В является касательным к силовой линии, он коллинеарен векторному элементу dl этой линии. Поэтому

=

= В 2p a

Рис. 6.7. Силовые линии магнитного поля прямого токи

Так как контур С охватывает всего один провод с током I, теорема (6.8) приводит к равенству

Отсюда найдем, что на расстоянии а от бесконечного прямого провода с током I индукция создаваемого им магнитного поля будет

Взаимодействие токов

Рассмотрим два тонких параллельных друг другу прямых провода с токами I₁и I₂ (рис. 6.8.). Если расстояние R между проводами много меньше их длины, то магнитную индукцию поля, создаваемого первым проводом на этом расстоянии, можно найти по формуле (6.15):

Направление вектора В₁ связано с направлением тока I₁ правилом пра­вого винта. Этот вектор изображен на рис. 6.8.

Рис. 6.8. Взаимодействие токов

Магнитное поле, создаваемое первым током, будет действовать на вто­рой провод с силой Ампера F₂₁, которая определяется формулой (5.8):

Подставив выражение (6.16) в формулу (6.18), получим следующее выра­жение для силы, с которой первый провод действует на участок второго провода длины l:

Итак, установлено, что параллельные провода с токами, текущими в одном направлении, притягиваются. Нетрудно доказать, что провода с токами, текущими в противоположных направлениях, отталкиваются друг от друга.

Источник

6.4. Магнитное поле соленоида

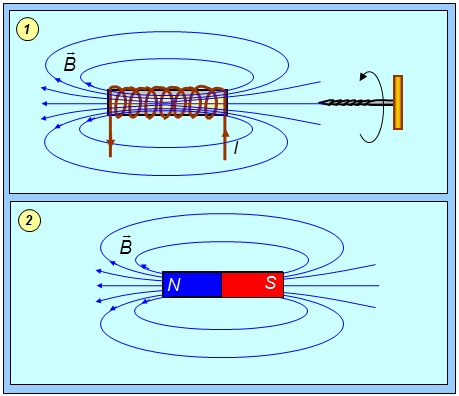
Соленоидом называется цилиндрическая катушка, состоящая из большого числа витков провода, образующих винтовую линию (рис. 6.23-1).

Рис. 6.23. Магнитные силовые линии поля: 1 — соленоида; 2 — полосового магнита

Магнитное поле соленоида напоминает поле полосового магнита (рис. 6.23-2).

Если витки намотаны вплотную, то соленоид — это система круговых токов, имеющих одну ось.

Если считать соленоид достаточно длинным, то магнитное поле внутри соленоида однородно и направлено параллельно оси. Вне соленоида вдали от краев магнитное поле также должно иметь направление параллельное оси и на большом расстоянии от соленоида должно быть очень слабым. Поле убывает по закону

Подсчитаем поле внутри соленоида. Возьмем элемент соленоида длиной dh, находящийся на расстоянии h от точки наблюдения. Если катушка имеет n витков на единицу длины, то в выделенном элементе содержится ndh витков. Согласно формуле (6.11), этот элемент создает магнитное поле

Интегрируя по всей длине соленоида, получаем

Таким образом, поле в бесконечно длинном соленоиде дается выражением

На практике соленоиды бесконечно длинными не бывают. Для иллюстрации рассмотрим некоторые примеры.

Пример 1. Найти магнитное поле в середине соленоида конечной длины l (рис. 6.24). Сравнить с полем бесконечно длинного соленоида. При каких условиях разница составляет менее 0,5 %?

Рис. 6.24. Магнитное поле катушки конечной длины
В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки

Решение. Магнитное поле в средней точке оси соленоида конечной длины l дается тем же интегралом (6.19), но с другими пределами интегрирования

Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна

По условию эта разница мала: 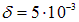, то есть мало отношение диаметра соленоида к его длине: 2R/l > R имеем

Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.

Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.

На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.

Рис. 6.25. Визуализация силовых линий магнитного поля

Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.

Источник

Магнитное поле соленоида

Величину индукции магнитного поля внутри бесконечно длинного соленоида можно определить, используя теорему о циркуляции вектора :циркуляция вектора по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на магнитную постоянную μ_о:

, (20)

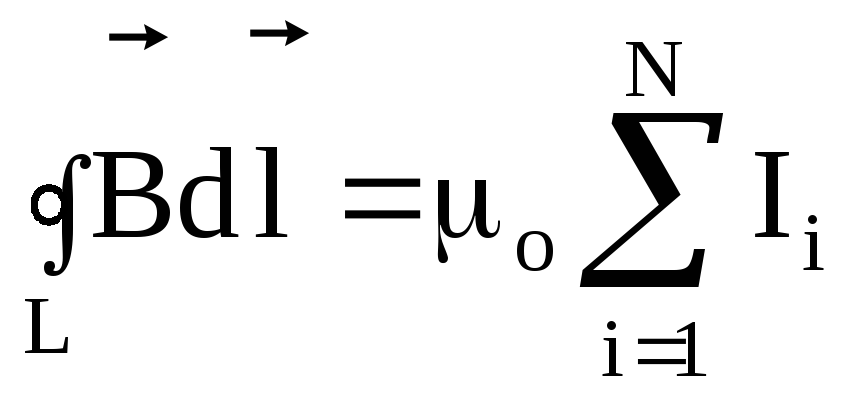
Рис.6. Магнитное поле соленоида

Для определения величины магнитной индукции В внутри соленоида выберем замкнутый контур ABCD прямоугольной формы, где 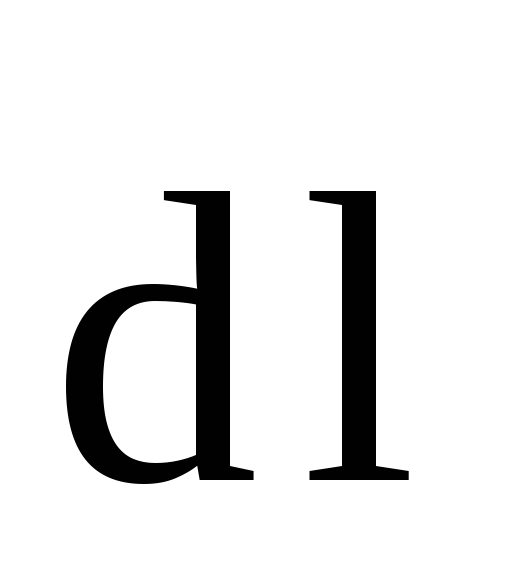— элемент длины контура, задающий направление обхода (рис.6). При этом длиныAB и CD будем считать бесконечно малыми.

Тогда циркуляция вектора по замкнутому контуруABCD, охватывающему N витков, равна:

(21)

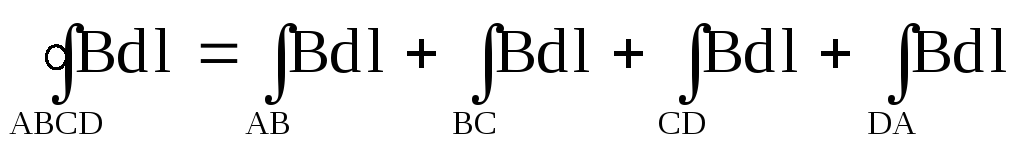
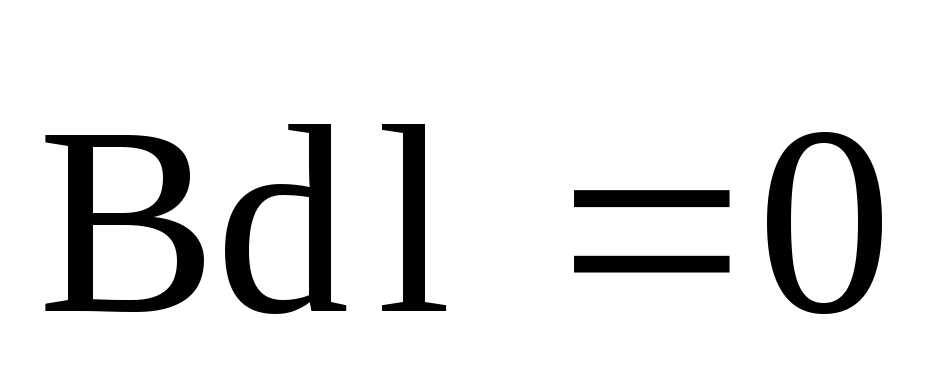
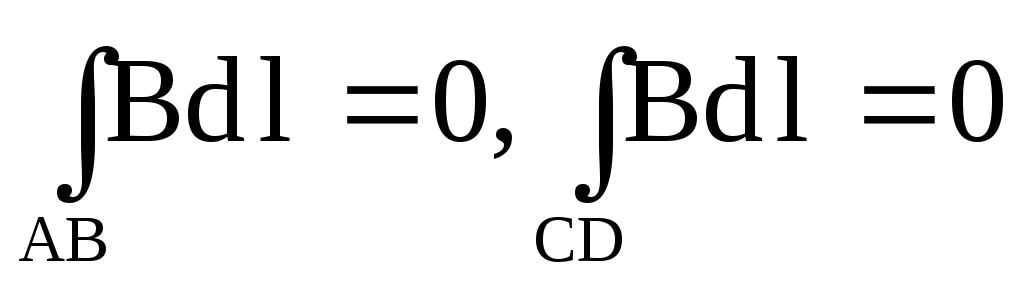
На участках AB и CD произведение , так как вектораивзаимно перпендикулярны. Поэтому

. (22)

На участке DA вне соленоида интеграл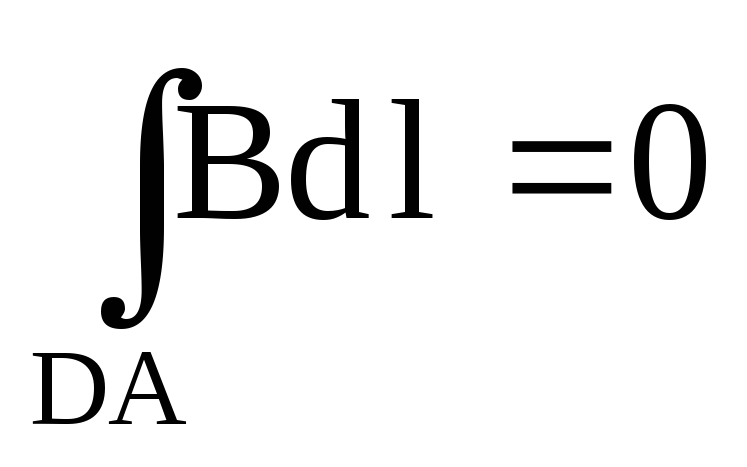, так как магнитное поле вне контура равно нулю.

Тогда формула (21) примет вид:

, (23)

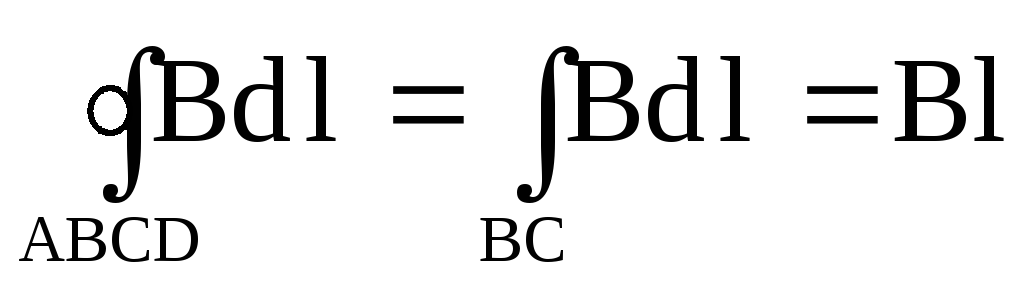
где l – длина участка BC. Сумма токов, охватываемых контуром, равна

, (24)

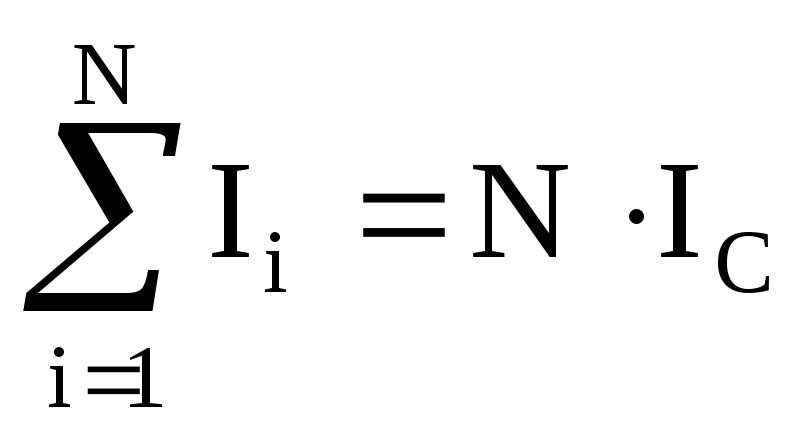
где I_c – сила тока соленоида; N – число витков, охватываемых контуром ABCD.

Подставив (23) и (24) в (20), получим:

. (25)

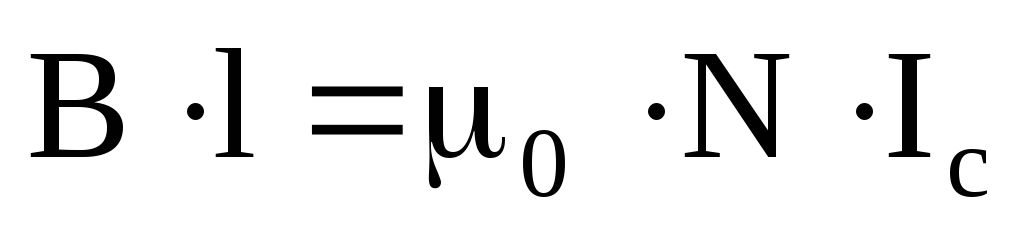
Из (25) получим выражение для индукции магнитного поля бесконечно длинного соленоида:

. (26)

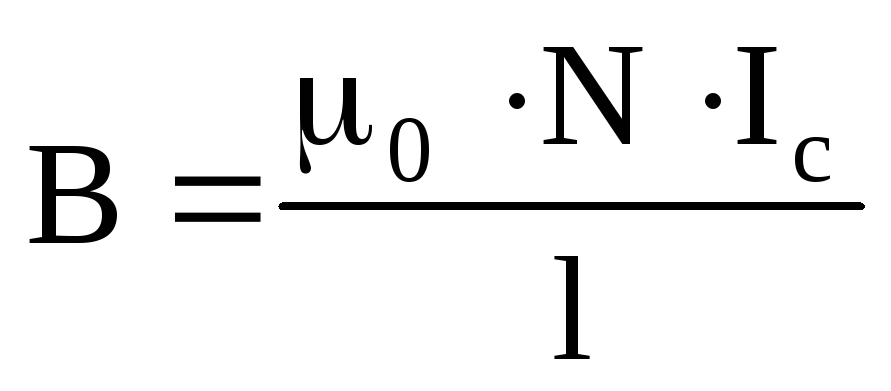
Так как число витков на единицу длину соленоида n равно:

(27)

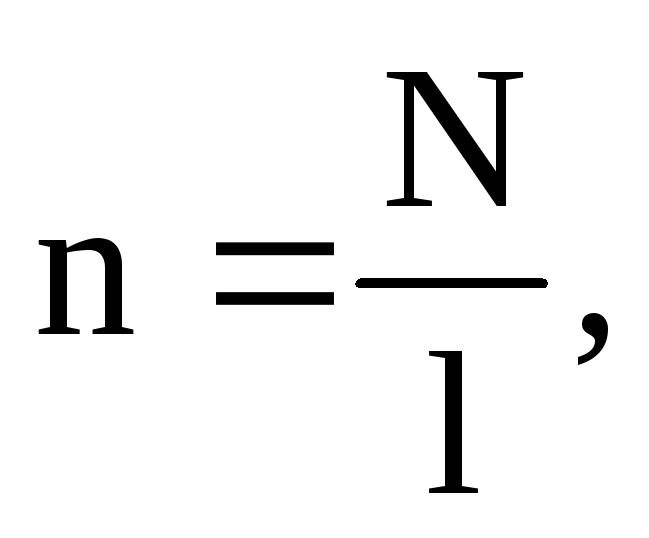
то окончательно получим:

. (28)

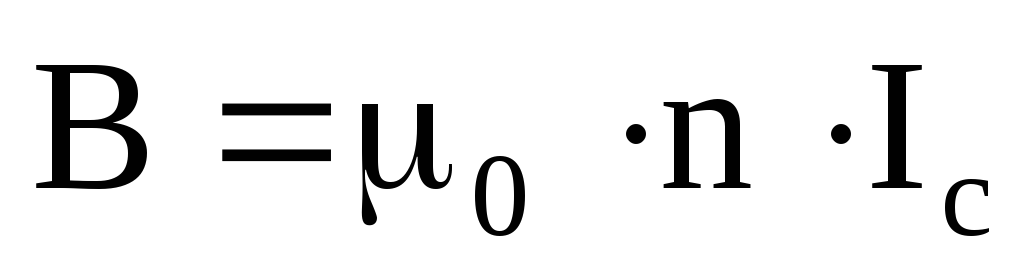
Если внутрь соленоида помещен сердечник, то формула (28) для В примет вид:

. (29),

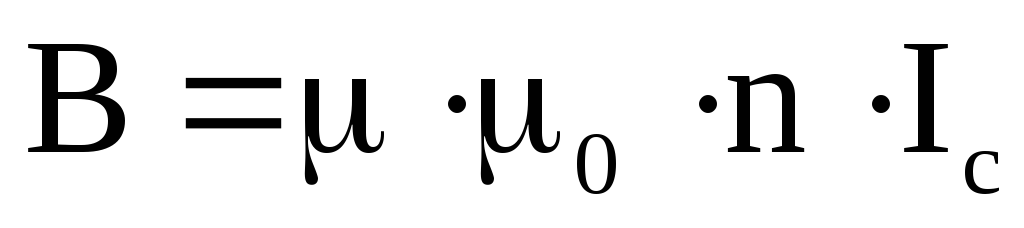
Таким образом, индукция В магнитного поля соленоида определяется током соленоида I_c, числом витком n на единицу длины соленоида и магнитной проницаемостью материала сердечника.

Цилиндрический магнетрон

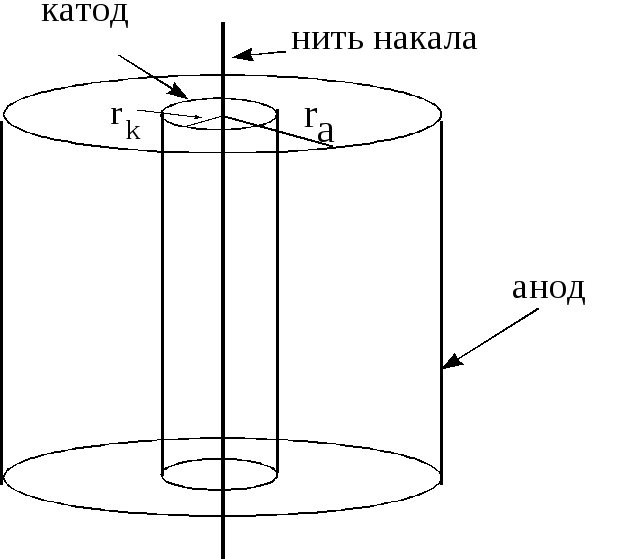
Магнетроном называется двухэлектродная электронная лампа (диод), содержащая накаливаемый катод и холодный анод и помещенная во внешнее магнитное поле.

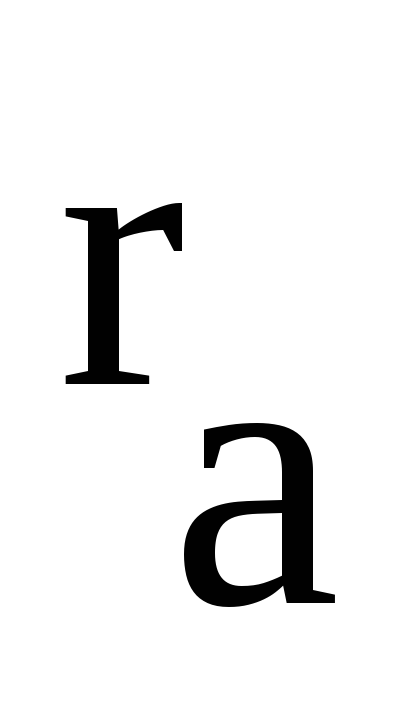
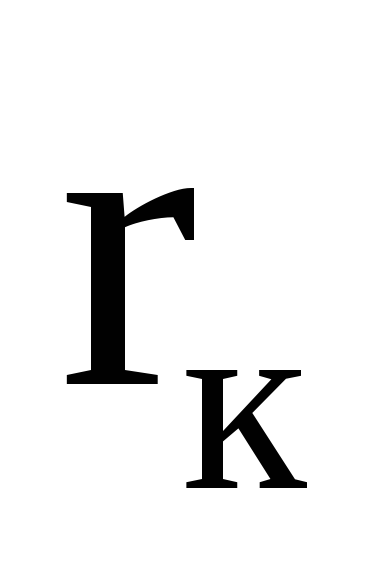
Анод диода имеет форму цилиндра радиусом . Катод представляет собой полый цилиндр радиусом, вдоль оси которого расположена нить накала, как правило, изготавливаемая из вольфрама (рис.7).

Раскалённый катод в результате явления термоэлектронной эмиссии испускает термоэлектроны, которые образуют вокруг катода электронное облако. При подаче анодного напряжения (рис.8), электроны начинают перемещаться от катода к аноду вдоль радиусов, что приводит к возникновению анодного тока. Анодный ток регистрируется миллиамперметром.

Рис.8. Электрическая схема цепи

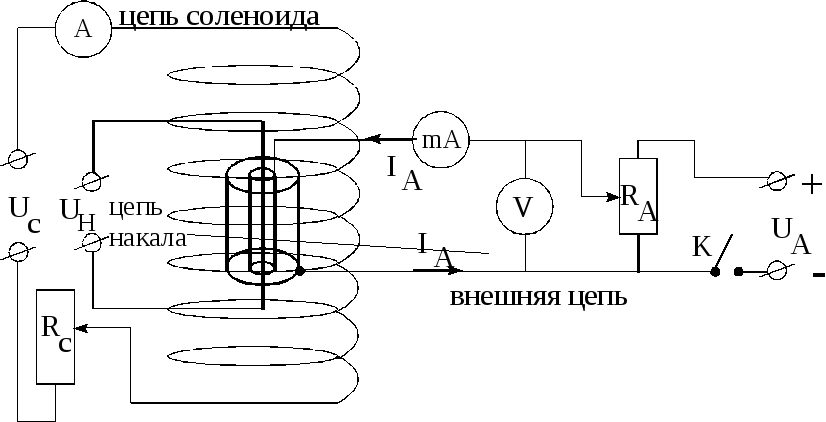
Величина анодного напряжения регулируется потенциометром R_A. Чем больше анодное напряжение, тем большее количество электронов за единицу времени достигает анода, следовательно, тем больше анодный ток.

Напряжённость электрического поля Е между катодом и анодом такая же, как и в цилиндрическом конденсаторе:

, (30)

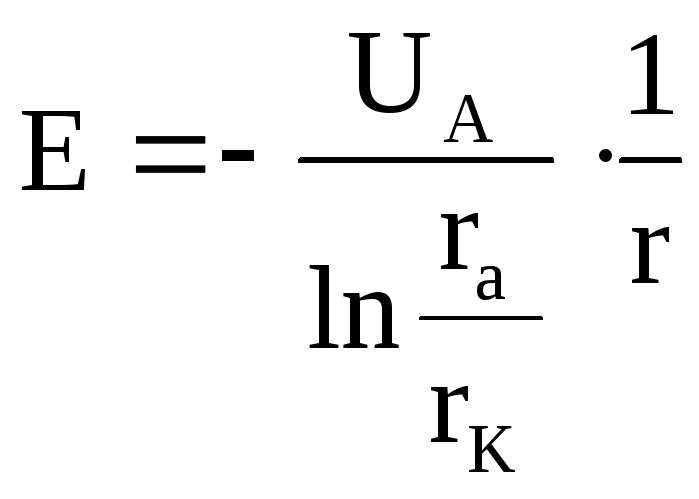
где r – расстояние от оси катода до данной точки пространства между катодом и анодом.

Из формулы (30) следует, что напряжённость поля Е обратно пропорциональна расстоянию r до оси катода. Следовательно, напряженность поля максимальна у катода.

r_к В_кр электроны не попадают на анод (рис.9), и анодный ток также будет равен нулю (рис.9, кривая 1).

Однако на практике, вследствие некоторого разброса скоростей электронов и нарушения соосности катода и соленоида, анодный ток уменьшается не скачком, а плавно (рис.9, кривая 2). При этом значение силы тока соленоида, соответствующее точке перегиба на кривой 2, считается критическим I_кр. Критическому значению тока соленоида соответствует анодный ток, равный:

, (33)

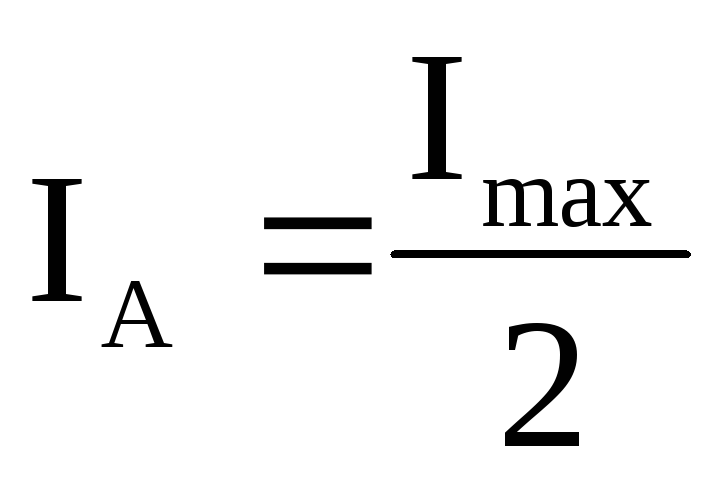
где 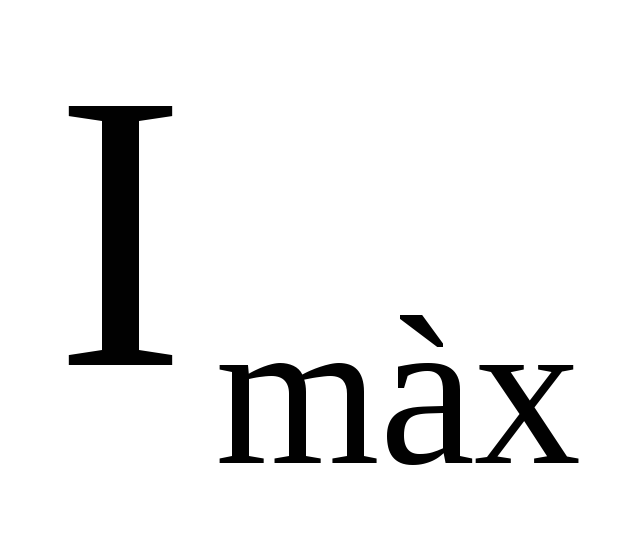– максимальное значение анодного тока при В = 0.

Зависимость анодного тока I_A от величины индукции магнитного поля В (или от тока в соленоиде) при постоянном анодном напряжении и постоянном накале называется сбросовой характеристикой магнетрона.

Источник