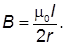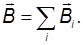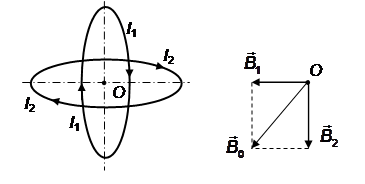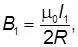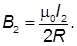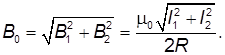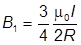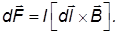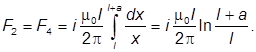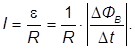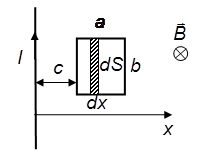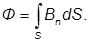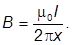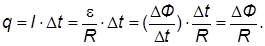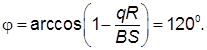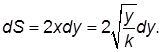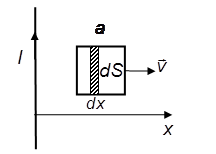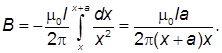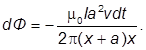поле бесконечно длинного провода

Источники магнитного поля

В школьной физике в качестве источников магнитного поля рассматриваются постоянные магниты и проводники с током. Если постоянные магниты мы уже рассмотрели, то с проводниками давайте разберёмся в данном разделе. Простейшие формы проводников для расчёта магнитных полей:

Для каждого из этих проводников можно рассчитать напряжённость магнитного поля в точке.

Итак, движущийся заряд создаёт вокруг себя магнитное поле. Самый простой тип движущегося заряда — это обычный электрический ток. Вопрос только в том, как согнуть проводник:

Рис. 1. Магнитное поле бесконечного проводника

Итак, возьмём бесконечный прямолинейный проводник с током. Слово «бесконечный» в данном случае небольшое приближение. Так для любой точки, находящейся непосредственно вблизи любого линейного проводника, сам проводник «кажется» бесконечным. Пусть по нашему проводнику течёт ток (рис. 1). Прямолинейный проводник с током создаёт вихревое (круговое) магнитное поле вокруг себя. Направление вектора магнитной индукции задаётся правилом буравчика (правилом правой руки). Исходя из этого правила, найдём направление вектора (рис. 2).

Рис. 2. Магнитное поле бесконечного проводника (магнитная индукция)

Для подсчёта модуля вектора магнитной индукции поля вне прямолинейного бесконечного проводника с током можно использовать соотношение (рис. 3):

Рис. 3. Модуль вектора магнитной индукции бесконечного линейного проводника

3D модели рисунков достаточно сложны для рассмотрения, поэтому введены условные обозначения для направлений векторов/токов в трёхмерном пространстве (рис. 4).

Рис. 4. Схематические отображения векторов

Тогда перерисуем рисунок 3, в случае, если мы смотрим сверху провода (рис. 5.1). В этом случае ток течёт на нас, т.е. из рисунка. И в случае, когда мы смотрим на провод снизу вверх (рис. 5.2). В этом случае ток течёт от нас, т.е. внутрь рисунка.

Рис. 5. Поле проводника (вид сверху)

На рисунке 5 точечной линией обозначено магнитное поле прямолинейного тока (оно круговое). Направление вектора магнитной индукции ( ) определяется правилом буравчика (правилом правой руки).

Правило буравчика для прямолинейного тока: правой рукой обхватываем проводник с током, отогнутый большой палец сонаправляем с током, тогда согнутые 4 пальца показывают направление вектора магнитной индукции.

Второй вариант системы, в которой достаточно просто рассчитать модуль вектора магнитной индукции, — это круговой виток с током. Т.е. сам проводник с током представляет собой окружность. По данному проводнику ток может течь как по часовой стрелке (рис. 6.1), так и против часовой (рис. 6.2).

Рис. 6. Круговой виток с током

В целом, магнитное поле такого проводника достаточно сложное, однако для центра витка нахождение модуля вектора магнитной индукции не представляет проблем:

Немного о — относительной магнитной проницаемости среды. Это параметр, который описывает насколько сама среда воспринимает магнитное поле источника. В целом, это табличная величина.

Правило буравчика для кругового тока: обнимаем правой рукой провод, большой отогнутый палец правой руки направляем по току, тогда загнутые 4 пальца будут указывать направление вектора магнитной индукции.

Важно: для наших систем можно запомнить, что прямолинейный ток создаёт круговое магнитное поле (рис.5), а круговой ток создаёт прямолинейное магнитное поле (рис.6).

Вывод: для поиска модуля вектора магнитной индукции достаточно проанализировать систему в задаче и описать её через модель бесконечного прямолинейного или кругового проводника с током.

Источник

Нормальное поле бесконечно длинного кабеля.

При теоретических расчетах и анализе физических явлений в методе ДК в качестве источника поля принимают весьма длинные заземленные линии, а анализ поля проводят вблизи кабеля. Нормальное поле такого длинного кабеля можно используют при количественной интерпретации.

Особый интерес представляет поле бесконечно длинного кабеля, расположенного на поверхности Земли. Токами смещения в Земле и в воздухе пренебрегают. Ось х совпадает с направлением кабеля. На поверхности Земли (z = 0) рассчитывают потенциал поля А_х, вертикальную составляющую магнитного поля Н_z, горизонтальные составляющие магнитного Н_у и электрического Е_х полей, обусловленные наличием электрического тока в нижнем проводящем полупространстве.

Потенциал и компоненты электромагнитного поля бесконечно длинного кабеля на поверхности Земли (z = 0) определяются по формулам:

Е_х = wmf(ϰ, y); (107)

H_z = f₁(ϰ, y); (108)

H_y = f₂(ϰ, y); (109)

A_х = f₃(ϰ, y); (110)

Для анализа удобно ввести электрические и магнитные числа электромагнитного поля в виде:

e_х = f(ϰ, y) = 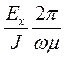; (111) h_z = f₁(ϰ, y) = ; (112)
h_y = f₂(ϰ, y) = . (113)

Рассчитаны и построены графики их амплитуд и фаз (т.е. модулей и аргументов) в зависимости от квадрата приведенного расстояния, т.е. от параметра р 2 = |ϰ 2 y 2 |, где у – расстояние от точки наблюдения до кабеля на поверхности Земли (рис. 16).

На рис. 16 представлены также графики амплитуды А * и сдвига фаз φ * для потенциала поля.

Рис. 16б. Графики амплитуд и фаз потенциала, электрических и магнитных чисел компонент электромагнитного поля БДК.

Рассмотрим поведение поля кабеля в области, где |ϰy| > 1.

Принято называть зону |ϰy| > 1 – дальней или волновой. В воздухе, где ϰ₀ ≈ 0, величина |ϰ₀y| в обеих зонах остается очень малой, поэтому поле на земной поверхности и в воздухе лишено характерных волновых черт не только в ближней, но и в дальней зоне. Приведенная классификация зон имеет реальный смысл только в земле, где в ближней зоне поле квазистационарное, а в дальней зоне, оно приближается к полю плоской волны, распространяющейся вертикально сверху вниз. По графикам электрических и магнитных чисел и их асимптотическим выражениям можно определить основные закономерности поведения поля кабеля.

Составляющая магнитного поля Н_у, отсутствующая в однородном пространстве, при убывании расстояния до кабеля стремится к постоянной величине ϰ и сдвинута относительно тока в кабеле на угол p/4. При увеличении частоты поля величина Н_у растет пропорционально .

При |ϰy| >> 1 компоненты Е_х и Н_z убывают по экспоненциальному закону, горизонтальный компонент магнитного поля Н_у убывает как 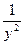, т.е. медленнее, его фаза стремится к углу p/4.

Рассчитаны и построены графики величин, получаемых по методике эллиптически поляризованного поля (рис. 17).

На этих графиках изображены магнитные числа большой и малой полуосей (а * и b * ), угол наклона большой полуоси эллипса к горизонту (α) и ее фаза (φ_а) относительно тока в источнике. Магнитные числа большой и малой полуосей эллипса поляризации связанны с самими полуосями соотношениями:

а = и b = , (114)

Приведенные величины полностью определяют эллиптически поляризованное тело. При малых значениях р 2 большая полуось эллипса поляризации наклонена под углом 90 0 к горизонту, а при увеличении р 2 величина α стремится к нулю (α ® 0).

При малых р 2 величина фазы большой полуоси эллипса поляризации φ_а синфазная с питающим током, а при р 2 ® 100 величина фазы φ_а ® 45 0 по отношению к фазе питающего тока.

Источник

6.2. Магнитное поле прямолинейного проводника с током

Вычислим поле, создаваемое током, текущим по тонкому прямолинейному проводу бесконечной длины.

Индукция магнитного поля в произвольной точке А (рис. 6.12), создаваемого элементом проводника dl, будет равна

Рис. 6.12. Магнитное поле прямолинейного проводника

Поля от различных элементов имеют одинаковое направление (по касательной к окружности радиусом R, лежащей в плоскости, ортогональной проводнику). Значит, мы можем складывать (интегрировать) абсолютные величины

Выразим r и sin через переменную интегрирования l

Тогда (6.7) переписывается в виде

Картина силовых линий магнитного поля бесконечно длинного прямолинейного проводника с током представлена на рис. 6.13.

Рис. 6.13. Магнитные силовые линии поля прямолинейного проводника с током:
1 — вид сбоку; 2, 3 — сечение проводника плоскостью, перпендикулярной проводнику

Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):

Рис. 6.14. Обозначения направления тока в проводнике

Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):

Напомним выражение для напряженности электрического поля тонкой нити, заряженной с линейной плотностью заряда

Сходство выражений очевидно: мы имеем ту же зависимость от расстояния до нити (тока), линейная плотность заряда заменилась на силу тока. Но направления полей различны. Для нити электрическое поле направлено по радиусам. Силовые линии магнитного поля бесконечного прямолинейного проводника с током образуют систему концентрических окружностей, охватывающих проводник. Направления силовых линий образуют с направлением тока правовинтовую систему.

На рис. 6.15 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг прямолинейного проводника с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.

Вокруг прямого провода, перпендикулярного пластинке, наблюдаются кольцевые силовые линии, расположенные наиболее густо вблизи провода. При удалении от него поле убывает.

Рис. 6.15. Визуализация силовых линий магнитного поля вокруг прямолинейного проводника

На рис. 6.16 представлены опыты по исследованию распределения силовых линий магнитного поля вокруг проводов, пересекающих картонную пластинку. Железные опилки, насыпанные на пластинку, выстраиваются вдоль силовых линий магнитного поля.

Рис. 6.16. Распределение силовых линий магнитного поля
вблизи пересечения с пластинкой одного, двух и нескольких проводов

Источник

Поле бесконечно длинного провода

Магнитная индукция в точке О определим по принципу суперпозиции магнитных полей, создаваемых прямолинейными участками I и II и полуокружностью III

б) Согласно принципу суперпозиции магнитных полей результирующая магнитная индукция в точке О будет складываться из магнитных индукций, создаваемых из трех участков провода в отдельности

Магнитная индукция поля, создаваемого отрезком проводника

Магнитная индукция поля, создаваемого круговым током в центре (точка О):

Результирующая индукция поля в точке О:

Индукция поля, создаваемого отрезком проводника, равна

Следовательно, результирующая индукция поля в точке О:

$B = \frac <4 \pi \cdot 10^<-7>\cdot 50 > <8 \pi \cdot 0,1>(3 \cdot 3,14 + 2) = 2,86 \cdot 10^ <-4>Тл$

г) В соответствии с принципом суперпозиции магнитная индукция в точке О равна:

$dB_ <1>= \frac < \mu_<0>I \sin \alpha > <4 \pi R^<2>/ \sin^ <2>\alpha > \frac < \sin^<2>\alpha > = \frac< \mu_<0>I > <4 \pi R>\sin \alpha d \alpha$

Подставим выражения (2) в (3) в формулу (1) получаем:

Раскрывая энак модуля в выражении (4) получаем:

д) В соответствии с принципом суперпозиции магнитная индукция в точке О равна:

$dB_ <1>= \frac < \mu_<0>I \sin \alpha > <4 \pi R^<2>/ \sin^ <2>\alpha > \frac < \sin^<2>\alpha > = \frac< \mu_<0>I > <4 \pi R>\sin \alpha d \alpha$

Подставляя выражение (3) и (2) в формулу (1) получаем:

е) В соответствии с принципом суперпозиции магнитная индукция в точке О равна:

Как следует из рисунка

С учетом этих соотношений формула (3) примет вид:

Подставляя выражения (2) и (4) в формулу (1) получаем:

Источник

Индукция магнитного поля прямого и

Кругового проводника с током

Основные формулы и законы

Магнитнаяиндукциия поля бесконечного прямолинейного проводникас током I в вакууме на расстоянии r от проводника

где 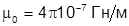– магнитная постоянная

Магнитная индукция в центре кругового витка с током

Магнитная индукция на оси кругового витка с током на расстоянии х от центра витка

Магнитная индукция поля, создаваемого отрезком проводника

Магнитная индукция внутри соленоида вдали от его концов

Принцип суперпозиции

Примеры решения задач

Индукция магнитного поля кругового тока I₁ в центре петли (в точке О) по величине равна

а тока I₂ соответственно

Направления векторов 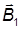и указаны на рис. 7.1 и составляют между собой прямой угол.

Результирующая индукция в точке О равна

Отсюда искомые величины:

Задача 7.2. Найти величину индукции магнитного поля в центре петли радиусом R = 10 см = 0,1 м, образованной бесконечно длинным тонким проводником с током I = 50 А.

Решение

Вектор индукции магнитного поля бесконечно длинного прямолинейного проводника с током на расстоянии r от него по величине равен

и направлен в центре (точке О) петли перпендикулярно ее плоскости на нас.

Вектор индукции магнитного поля кругового тока в центре петли по направлению совпадает с и по величине равен

Индукции поля, создаваемого проводником и круговым током в центре петли равна

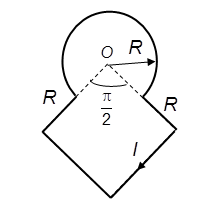
Задача 7.3. По плоскому контуру из тонкого провода течет ток I. Определить магнитную индукцию поля, создаваемого этим током в точке О. Радиус изогнутой части контура равен R.

Решение

Разобьем нашу фигуру на 5 частей: часть окружности и 4 стороны квадрата. От каждой из частей определим направление вектора магнитной индукции. Вектор индукции от 3/4 части окружности равен

и направлен в точке 0 перпендикулярно ее плоскости от нас.

Так как точка О лежит на оси проводников 2 и 5, то .

Векторы магнитной индукции, создаваемые проводниками 3 и 4, будут в точке О направлены перпендикулярно плоскости чертежа от нас. В силу симметрии задачи вклад от этих двух проводников будет одинаковым. Для определения значения магнитной индукции от проводника 3 воспользуемся формулой для отрезка проводника:

Для нашего случая магнитная индукция, создаваемая проводником 3, равна:

Согласно принципу суперпозиции

Таким образом, в точке О значение магнитной индукции равно

Сила Лоренца, сила Ампера

Основные формулы и законы

Магнитная сила (сила Лоренца):

Полная сила, действующая на заряд:

Сила Ампера:

Магнитная индукция поля бесконечного прямолинейного проводникас током I в вакууме на расстоянии r от проводника:

Магнитная индукция в центре кругового витка с током

Примеры решения задач

Задача 7.4. В поле прямого провода с током I в одной плоскости с ним находится квадратная рамка с током i и стороной a так, что две ее стороны параллельны проводу. Ближайшая сторона рамки находится на расстоянии 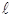от провода. Определить силу Ампера, действующую на рамку.

Решение

Прямой провод с током создает вокруг себя магнитное поле. Направление вектора индукции магнитного поля показано на рис. 7.4. Каждая из сторон рамки, являющаяся проводником с током i, находится в магнитном поле провода, поэтому, на каждую из сторон рамки действует сила Ампера, лежащая в плоскости, перпендикулярной вектору индукции, и направленная перпендикулярно стороне (см. рис. 7.5).

Поскольку угол между направлением тока в рамке и вектором индукции прямой, то силы Ампера, действующие на стороны 1 и 3, равны, cоответственно

где В₁ и В₃ – значения магнитной индукции в местах, где расположены стороны рамки 1 и 3.

В силу симметрии задачи, ясно, что силы, действующие на стороны рамки 2 и 4, равны между собой.

Для определения значений сил, действующих на стороны рамки 2 и 4, выделим малый участок рамки шириной dx, в пределах которого значение магнитной индукции будем считать равным

Элементарная сила Ампера, действующая на малый участок, равна

Результирующая сила, действующая на рамку:

Поскольку силы, действующие на стороны 2 и 4, компенсируют друг друга, то результирующая сила будет равна

и направлена в сторону прямого провода.

Электромагнитная индукция

Основные формулы и законы

Магнитный поток

Магнитный поток через поверхность равен

ЭДС электромагнитной индукции

Индукционный ток в замкнутом проводящем контуре:

ЭДС электромагнитной индукции при движении прямолинейного проводника в однородном магнитном поле перпендикулярно силовым линиям:

Если проводник движется под углом a к силовым линиям поля, то ЭДС индукции будет определяться соотношением:

.

Магнитный поток, охватываемый контуром, пропорционален силе тока в проводнике:

Индуктивность соленоида:

ЭДС самоиндукции в проводнике в отсутствие ферромагнетиков (L = const):

Магнитная энергия, запасенная в соленоиде:

Примеры решения задач

Задача 7.5. В одной плоскости с бесконечно длинным прямым проводом, по которому течет ток I, расположена прямоугольная рамка размером а х b так, что большие стороны ее длиной b параллельны проводу, а расстояние от провода до ближайшей из этих сторон равно с. Определите магнитный поток, пронизывающий рамку.

Решение

Магнитный поток через поверхность площади рамки равен

Вектор магнитной индукции 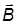перпендикулярен плоскости рамки, поэтому для всех точек плоскости рамки . Магнитная индукция, создаваемая бесконечно длинным прямым проводником с током, определяется формулой

Для вычисления магнитного потока заметим, что так как В зависит от х, то и элементарный поток будет зависеть от х, где х – расстояние от провода до точки, в которой определяется В:

Разобьем площадь рамки на узкие элементарные площадки длиной b, шириной dx и площадью dS = bdx. В пределах этой площадки магнитную индукцию можно считать постоянной.

Тогда элементарный магнитный поток можно записать в виде:

Проинтегрировав данное выражение в пределах от с до с + а, найдем:

Решение

Выберем направление нормали к витку таким образом, чтобы в начальном положении она была перпендикулярна вектору 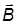. Тогда начальный поток будет равен

а после поворота на угол φ поток станет равен

Прошедший через виток заряд выражается через изменение потока

Определим изменение потока

Из последнего уравнения получим:

Искомый угол поворота равен:

Задача 7.7. Провод, имеющий форму параболы , находится в однородном магнитном поле с индукцией В, перпендикулярной плоскости параболы. Из вершины параболы в момент t = 0 начали двигать прямолинейную перемычку, параллельную оси х. Найти ЭДС индукции в образовавшемся контуре как функцию у, если перемычку перемещают с постоянной скоростью v.

Решение

При перемещении перемычки на расстояние dy увеличение площади контура равно:

Увеличение площади приводит к изменению магнитного потока через контур и, соответственно, к появлению ЭДС. Найдем ее.

В нашей задаче перемычку двигают с постоянной скоростью , поэтому

Окончательно, ЭДС индукции как функция координаты у будет иметь вид

Задача 7.8. Квадратная рамка со стороной а и длинный прямой провод с током I находятся в одной плоскости. Рамку поступательно перемещают с постоянной скоростью v. Найти ЭДС индукции в рамке как функцию расстояния х.

Решение

ЭДС индукции равна

В нашей задаче изменение магнитного потока идет не за счет изменения площади, а за счет изменения величины вектора В в зависимости от х.

Для бесконечного длинного провода:

Из последней формулы имеем:

Магнитный поток, пронизывающий рамку:

Площадь элементарной площадки:

Изменение магнитного потока через элементарную площадку:

Знак минус показывает, что с удалением от провода величина потока убывает. ЭДС индукции равна

Решение

При размыкании цепи ток в катушке начнет уменьшаться, что приведет к изменению магнитного потока, пронизывающего витки катушки. При этом в катушке возникнет ЭДС самоиндукции

Следовательно, за время уменьшения тока до нуля в катушке будет действовать ЭДС самоиндукции, среднее значение которой

Источник