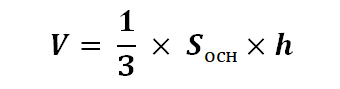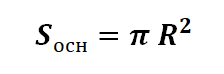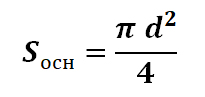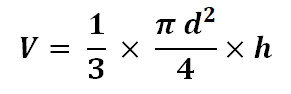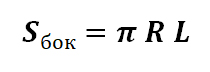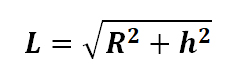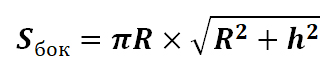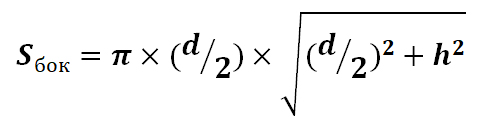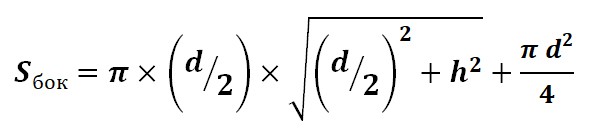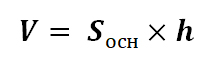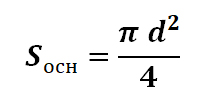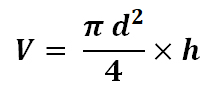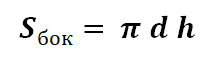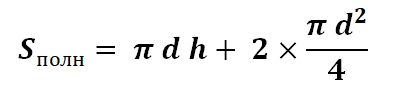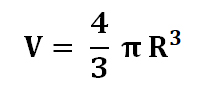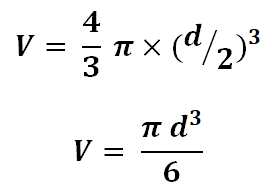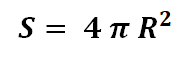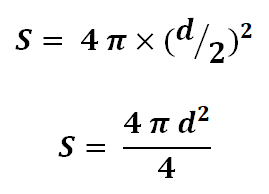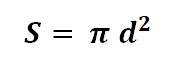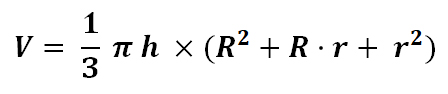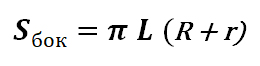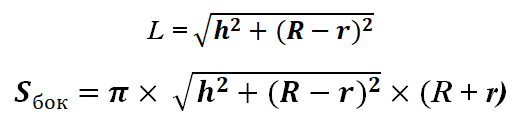площадь стен цилиндра калькулятор

Онлайн калькулятор. Площадь цилиндра.

Используя этот онлайн калькулятор, вы сможете найти площадь боковой поверхности цилиндра, а также площадь полной поверхности цилиндра.

Воспользовавшись онлайн калькулятором для вычисления площади поверхности цилиндра, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти площадь поверхности цилиндра

Введите значение радиуса цилиндра и его высоты

Ввод данных в калькулятор для вычисления площади цилиндра

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!

Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.

Дополнительные возможности калькулятора вычисления площади цилиндра

Теория. Площадь поверхности цилиндра

— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями (основаниями), пересекающими её.

Цилиндр называется круговым, если его основание – круг. Расстояние между основаниями – высота цилиндра.

Формулы для вычисления площади боковой поверхности цилиндра

Формулы для вычисления площади полной поверхности цилиндра

S = 2 π R h + 2 π R 2 = 2 π R ( R + h )

Источник

Калькулятор расчёта объёмов и площадей поверхности тел

Назначение калькулятора

Калькулятор позволяет рассчитать объёмы и площади поверхности таких геометрических тел, как конус, усечённый конус, шар и цилиндр.

В работе калькулятора используются следующие формулы:

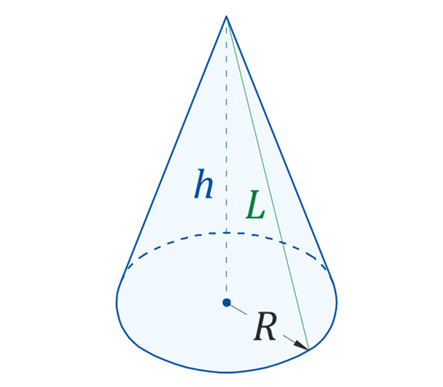
1. Конус

1.1 Объём конуса

Для расчёта объёма конуса применяется формула:

S_осн – площадь основания, которое представляет собой круг, соответственно его площадь может быть рассчитана по формуле:

R – радиус основания;

d – диаметр основания.

Тогда итоговая формула будет иметь вид:

1.2 Площадь поверхности конуса

Площадь боковой поверхности конуса может быть вычислена по формуле:

R – радиус основания;

L – образующая конуса;

Образующую можно выразить через радиус и высоту h:

Тогда формула площади боковой поверхности примет вид:

Чтобы вычислить полную площадь поверхности, необходимо к площади боковой поверхности добавить площадь основания конуса:

2. Цилиндр

2.1 Объём цилиндра

Объём цилиндра может быть вычислен по следующей формуле:

h – высота цилиндра;

S_осн> – площадь основания, которое представляет собой круг, соответственно его площадь может быть рассчитана по формуле:

Тогда итоговая формула будет иметь вид:

2.2 Площадь поверхности цилиндра

Площадь боковой поверхности цилиндра находится по формуле:

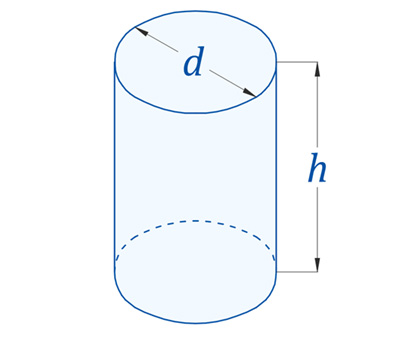
d – диаметр цилиндра;

h – высота цилиндра;

Для того, чтобы найти площадь полной поверхности цилиндра необходимо к площади боковой поверхности добавить две площади основания:

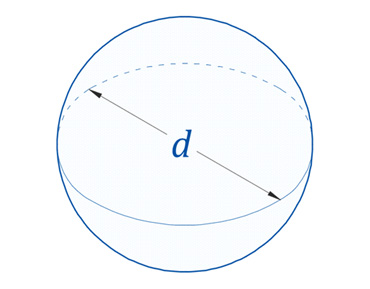
3. Шар (сфера)

3.1 Объём шара вычисляется по формуле:

Если радиус выразить через диаметр, то получим следующее:

3.2 Площадь поверхности шара вычисляется по формуле:

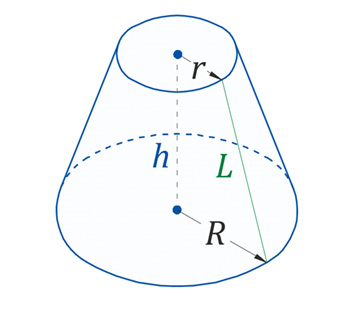
4. Усечённый конус

4.1 Объём усечённого конуса рассчитывается по формуле:

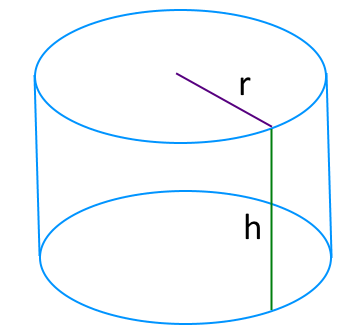
R – радиус нижнего основания;

r – радиус верхнего основания;

4.2 Площадь боковой поверхности усечённого конуса находится по формуле:

L – образующая усечённого конуса;

Если образующую выразить через высоту, то получим следующее:

Для того, чтобы вычислить площадь полной поверхности усечённого конуса необходимо к площади боковой поверхности добавить площади верхнего и нижнего основания:

Источник

Онлайн калькулятор площади цилиндра

С помощью данного бесплатного онлайн калькулятора вы сможете узнать площадь цилиндра (боковую и полную поверхности). Преимуществом сервиса является то, что перевод (конвертация) осуществляется автоматически. Просто вводите значения в соответствующие поля.

Площадь боковой поверхности цилиндра

Площадь всей поверхности цилиндра

Цилиндр – это геометрическое тело, которое ограничено двумя параллельными поверхностями, пересекающими цилиндрическую поверхность. Цилиндрическая поверхность называется боковой поверхностью цилиндра. Две параллельные поверхности называются основаниями цилиндра.

Как самостоятельно узнать площадь цилиндра?

Для вычисления площади цилиндра можно воспользоваться следующими двумя формулами:

1. Боковая поверхность через высоту и радиус:

Площадь цилиндра = 2 * Пи * Высота * Радиус (Пи = 3.141592653589793, чаще используют просто 3.14)

2. Полная поверхность через высоту и площадь:

Площадь цилиндра = 2 * Пи * Радиус * (Высота + Радиус) (Пи = 3.141592653589793, чаще используют просто 3.14)

Теперь, у вас всегда есть под рукой удобный и легкий калькулятор для расчетов.

Источник

Калькулятор для цилиндра

Онлайн калькулятор для цилиндра позволяет по известным данным вычислить:

Калькулятор для цилиндра: комментарий

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Обозначения для цилиндра:
R – радиус, D – диаметр,
V – объем,
Sо – площадь основания, Sб – площадь боковой поверхности, S – площадь полной поверхности,
h – высота прямого кругового цилиндра (h1 и h2 — минимальная и максимальная высота)
π – число Пи которое всегда примерно равно 3,14.

Прямой круговой цилиндр

Круговым называется цилиндр, если его направляющая является окружностью. Прямым называется цилиндр, если его образующая перпендикулярна основаниям.

Формулы для прямого кругового цилиндра:

Площадь(Sб) боковой поверхности прямого кругового цилиндра

Так как боковая поверхность представляет собой прямоугольник, то площадь боковой поверхности цилиндра определяется по формуле: Sб=2πR⋅h

Площадь(Sо) основания цилиндра

Площадь(S) полной поверхности прямого кругового цилиндра

Площадь полной поверхности цилиндра определяется по формуле: S=2πRh+2πR 2 =2πR(h+R)

Формулы нахождения радиуса и диаметра по:

Формулы нахождения высоты по:

Скошенный цилиндр

Прямой круговой цилиндр со скошенным основанием (скошенный цилиндр) определяется радиусом основания R, минимальной высотой h1 и максимальной высотой h2.

Источник

Калькулятор объёма цилиндра

Скачать, сохранить результат

Выберите способ сохранения

Информация

Теоретическая математика включает в себя невероятное количество формул, теорем, аксиом, законов и много другого. Достаточно большая часть знаний находит своё отражение в практическом мире. Строители, инженеры, механики, программисты и представители многих других сфер деятельности, часто оказываются в положении, когда необходимо посчитать тот или иной показатель по формуле. При этом на сотруднике может лежать большая ответственность за точность расчета.

Наши эксперты разработали онлайн калькулятор, который позволяет без затруднений получить значение любого показателя и при этом сохранив предельную точность. В нашем калькуляторе всегда демонстрируется применяемая формула, что позволяет специалисту проверить верность полученного значения.

Наш калькулятор предоставляет два варианта расчета объема цилиндра:

Для того, чтобы вычислить объем на нашем калькуляторе следует действовать следующим образом:

Используя наш калькулятор, Вы исключите возможность ошибки в расчетах, а также получите ряд преимуществ:

Таким образом, если у Вас когда-нибудь возникнет вопрос «Как узнать те или иные значения исходя из имеющихся данных?», то можете с уверенностью воспользоваться нашим калькулятором, которые точно посчитает, объяснит как посчитал и позволит Вам получить свои выгоды.

Источник