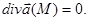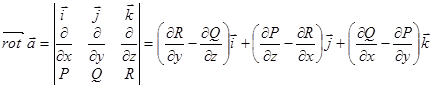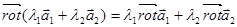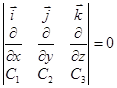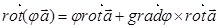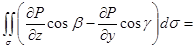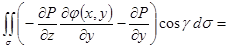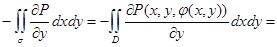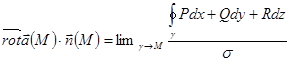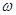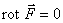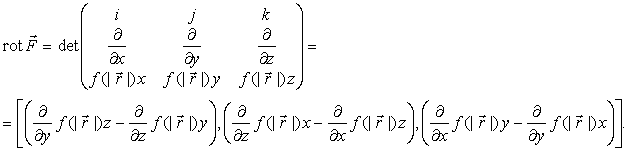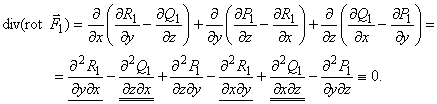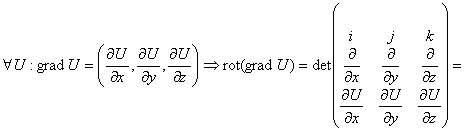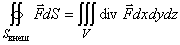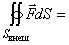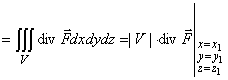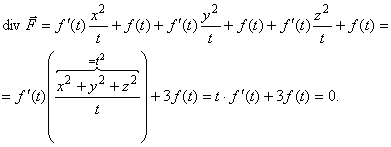определение дивергенции соленоидальное поле
Определение соленоидального поля



Соленоидальные поля
Векторное поле a называется соленоидальным, если в каждой его точке дивергенция равна нулю:
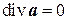
В связи с этим соленоидальные поля часто называют несжимаемым. Происхождение этого названия легко понять, если обратится к гидродинамическому смыслу дивергенции. Простейшим примером соленоидального поля является поле скоростей несжимаемой жидкости или магнитное поле.
Мы выяснили, что div rot jº0. Это значит, что если векторное поле является соленоидальным, то его можно представить в виде ротора некоторого поля A:
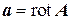
Вектор A называется векторным потенциалом данного поля. Отметим, что условие (8.28) необходимо, но, вообще говоря, не достаточно для существования векторного потенциала.
Поток соленоидального поля через любою замкнутую поверхность, целиком лежащей в области непрерывности поля, равен нулю:
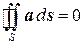
Эта формула является следствием теоремы Остроградского-Гаусса. Однако теорему Остроградского-Гаусса можно применить только для односвязных областей, т.е. только для поверхностей, которые можно стянуть в точку поля, не выходя за пределы поля.
Итак, векторное поле является соленоидальным тогда и только тогда, когда равен нулю поток через любою замкнутую поверхность, которую можно стянуть в точку, не пересекая его границ.
Отметим, что выполнение любого из условий (8.27)-(8.29) являются достаточными для того, чтобы векторное поле было соленоидальным, и выполнялись остальные условия.
Соленоидальное векторное поле
Содержание
Определение
Векторное поле называется соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю:

всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также бездивергентными.
Для широкого класса областей это условие выполняется тогда и только тогда, когда 


Проще говоря, поле является вихревым, если оно не имеет источников. Силовые линии такого поля не имеют ни начала, ни конца, и являются замкнутыми. Вихревое поле порождается не покоящимися зарядами (источниками), а изменением связанного с ним поля (например, для электрического поля порождается изменением магнитного). Поскольку в природе не существует магнитных зарядов, то магнитное поле всегда является вихревым, и его силовые линии всегда замкнуты. Силовые линии постоянного магнита, несмотря на то, что выходят из его полюсов (словно имеют источники внутри), на самом деле замыкаются внутри магнита. Поэтому, разрезав магнит надвое, не удастся получить два отдельных магнитных полюса.
Примеры
Этимология
См. также
Полезное
Смотреть что такое «Соленоидальное векторное поле» в других словарях:
Векторное поле — Векторное поле это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например, вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан… … Википедия
Потенциальное векторное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном… … Википедия
СОЛЕНОИДАЛЬНОЕ ПОЛЕ — векторное поле, не имеющее источников. Это означает, что дивергенция вектора а С. п. равна нулю: diva=0. Примером С. п. служит магн. поле, divB=0, где В вектор магнитной индукции. С. п. можно всегда представить в виде a=rot b; вектор b наз.… … Физическая энциклопедия
Соленоидальное поле — векторное поле, не имеющее источников. Это означает, что Дивергенция вектора а С. п. равна нулю: div а = 0. Примером С. п. служит Магнитное поле, div В = 0, где В вектор магнитной индукции (См. Магнитная индукция). С. п. можно всегда… … Большая советская энциклопедия
СОЛЕНОИДАЛЬНОЕ ПОЛЕ — трубчатое поле, векторное поле, не имеющее ни источников, ни стоков, т. е. дивергенция к рого равна нулю во всех его точках. Поток С. п. через любую замкнутую кусочно гладкую ориентированную границу любой области равен нулю. С. и. характеризуется … Математическая энциклопедия
Градиентное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
Потенциальное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
Теорема разложения Гельмгольца — Теорема разложения Гельмгольца утверждение о разложении произвольного дифференцируемого векторного поля на две компоненты: Если дивергенция и ротор векторного поля определены в каждой точке конечной открытой области V пространства, то всюду … Википедия
Векторный потенциал — У этого термина существуют и другие значения, см. Потенциал. Эта статья о математическом термине. О физическом см. векторный потенциал электромагнитного поля. В векторном анализе векторный потенциал это векторное поле,… … Википедия
Соленоидальное поле и его свойства.
Векторное поле 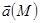
Свойства соленоидального поля.
1) Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю.
Необходимость следует из формулы Остроградского – Гаусса, достаточность – из инвариантного определения дивергенции.
2) Поток соленоидального поля через любую поверхность, окружающую изолированный источник или сток, один и тот же.

| Рассмотрим две замкнутых поверхности 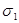 и и 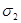 , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям. Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости. В той и другой области поле соленоидально. Следовательно, , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям. Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости. В той и другой области поле соленоидально. Следовательно, |
поток векторного поля через границы этих областей равен нулю.
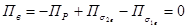
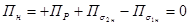
Складывая эти выражения, получим 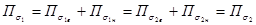
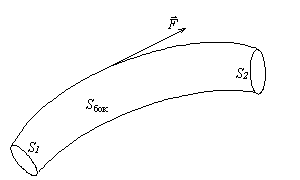
3) Поток соленоидального поля через произвольное сечение векторной трубки один и тот же.
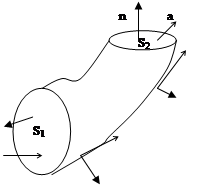 | Обозначим Sбок –боковую поверхность векторной трубки. На боковой поверхности направления нормали и векторного поля ортогональны, так как векторная трубка образована векторными линиями, а вектор поля направлен по касательной к векторной линии. Поэтому поток векторного поля через боковую поверхность векторной трубки равен нулю (ПSбок.= 0). Учитывая направления нормалей и вектора поля на сечениях векторной трубки S1 и S2, а также соленодальность поля, получим 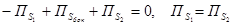 . . |
Следствие. Векторные линии соленоидального поля не могут начинаться и заканчиваться внутри поля.
В самом деле, иначе конечный поток приходился бы на нулевую площадь источника или стока, что требовало бы бесконечной мощности источника или стока.
Лекция 9 Формула Стокса.
Ротор векторного поля.
Назовем ротором векторного поля 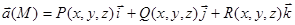
Свойства ротора.
1) Линейность
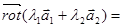
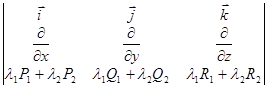
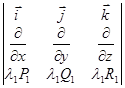
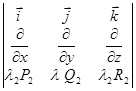
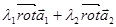
2) 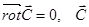
3)

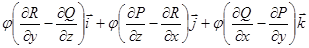
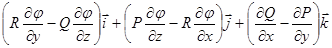
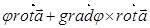
Теорема Стокса.
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность 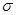
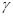
Пусть компоненты векторного поля 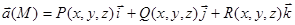
Тогда справедлива формула Стокса
Замечание. Нормаль к поверхности 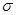
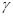
Доказательство теоремы Стокса.
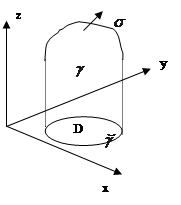  | Как и формула Остроградского – Гаусса, формула Стокса состоит из трех независимых частей (в силу произвольности компонент векторного поля). Докажем одну из этих частей, остальные формулы доказываются аналогично. Докажем 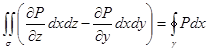 — часть формулы Стокса, в которой содержится только компонента P. Предположим, что поверхность — часть формулы Стокса, в которой содержится только компонента P. Предположим, что поверхность 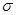 описывается уравнением описывается уравнением 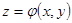 . Тогда нормаль к поверхности . Тогда нормаль к поверхности |
представляет собой вектор
Отсюда видно, что 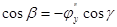
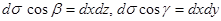

(на поверхности 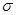
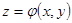
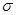
=
Используем формулу Грина для области D с ее границей 

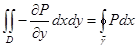
= 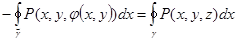
В самом деле, на контуре 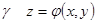

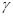
Одна из частей формулы Стокса доказана.
Линейным интеграломвекторного поля 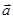
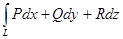
Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляциейвекторного поля называется линейный интеграл по замкнутому контуру.
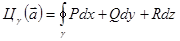
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
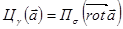
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора.
Рассмотрим произвольную точку M в области V. Проведем через нее поверхность 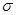
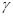
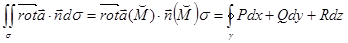
Здесь, как и ранее 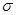
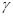
Это и есть инвариантное определение ротора.
Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором 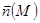
Если направление 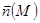
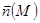
Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая.
Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью
Векторное поле линейной скорости 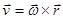
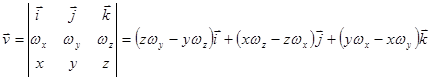
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.
Потенциальные, соленоидальные и
1. Потенциальное поле
Пусть есть две точки А и В.
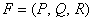
Поле называется потенциальным, если выполняется одно из условий:
1)
Поле 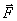
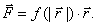
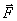
2. Соленоидальное поле
Поле 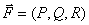
По формуле Гаусса–Остроградского:
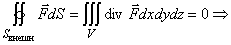
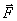
Поток через S 1 равен потоку через S 2 с обратным знаком – «сколько вошло, столько вышло».
Докажем также, что 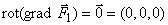
Рассчитаем площадь поверхности сферы:
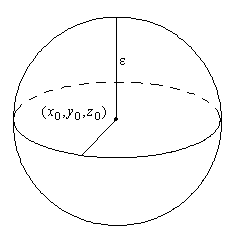
Перейдем к пределу:
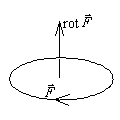
Ротор является инвариантом относительно системы координат.
3. Гармоническое поле
Гармоническим называется поле, для которого и ротор и дивергенция равны нулю.
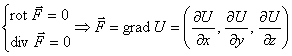
Это выражение – уравнение Лапласа. Его решением является гармоническая
функция, поэтому поле, обладающее такими свойствами, называется гармоническим.
В качестве примера рассмотрим гравитационное поле, которое является единственным центральным полем, одновременно имеющим свойства гармонического.
Докажем, что всякое центральное гармоническое поле – гравитационное и наоборот.