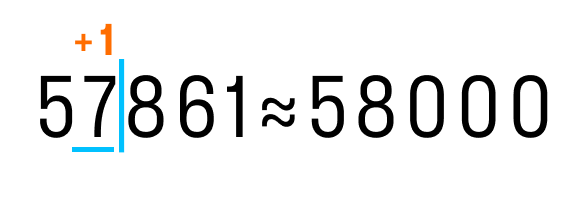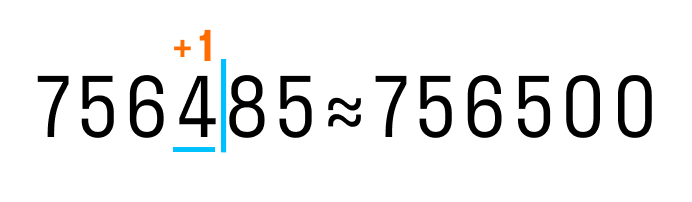Округлить до второй значащей цифры что это значит
Как правильно округлять числа после запятой
Далеко не все умеют округлять числа правильно. Например, купив товар за 1469 рублей, чаще всего люди говорят, что потратили полторы тысячи. В целом это так, но некоторые правила округления нарушаются. Чтобы этого избежать, мы с вами поговорим о том, как правильно работать с числами.
Зачем нужно округление
Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.
Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:
Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.
Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.
Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.
Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.
Правила округления чисел
В основе округления лежат математические правила:
В метрологии — науке об округлениях и погрешностях, результат принято округлять до двух значащих цифр. Что же это значит? Значащая цифра — это цифра от первой, отличной от нуля.
Есть три случая, для которых есть свои особенности округления:
Когда мы имеем дело с числами меньше единицы, необходимо округлять результат до двух знаков после запятой. Например, число 0,7342. Округляем это число до 0,734, а потом до 0,73. Именно так и должен быть округлён результат. Первый ноль не является значащей цифрой.
Попробуем округлить 8,357. Первая цифра 8 является значащей, так как она отлична от нуля. Соответственно, нам необходимо округлить результат до одного знака после запятой. Согласно правилам, о которых мы говорили выше, результат будет равен 8,4.
Теперь самый сложный случай. Попробуем округлить 47,336. Так как все цифры отличны от нуля, мы будем округлять результат до целого числа. По математическим правилам он будет равен 47. Если мы имеем дело с трёхзначным числом, необходимо округлить результат до двух знаков, после чего умножить на 10 в нужной степени. Пример: округляем 4289,346 и получаем 43, умноженное на десять в квадрате.
Именно для того и нужна метрология, чтобы правильно округлять и записывать результат в технической документации. А также для избежания ошибок при ведении расчетов в разработке технических устройств.
Заключение
Теперь вы знаете, как правильно округлять и сможете делать все необходимые расчеты самостоятельно. Главное, доходы округлять в меньшую сторону, а расходы — в большую. И тогда вам точно будет хватать денег на все покупки, и останется небольшая сумма, которую можно потратить на развлечения. Успехов вам!
Видео
В нашем видео подробно рассказано о правилах округления чисел — с примерами.
Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
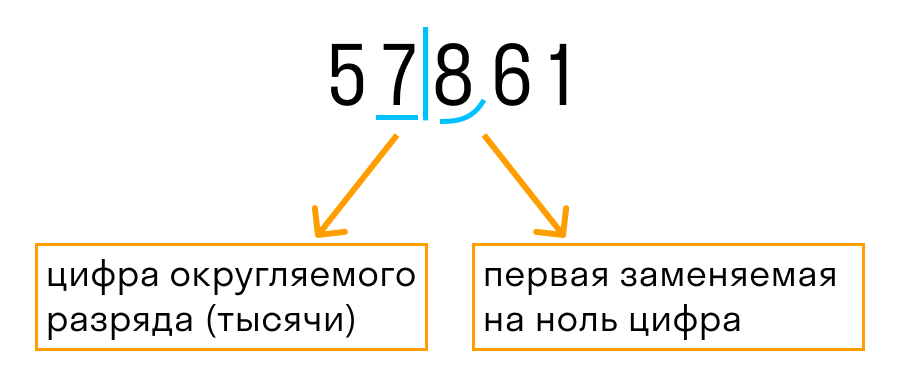
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
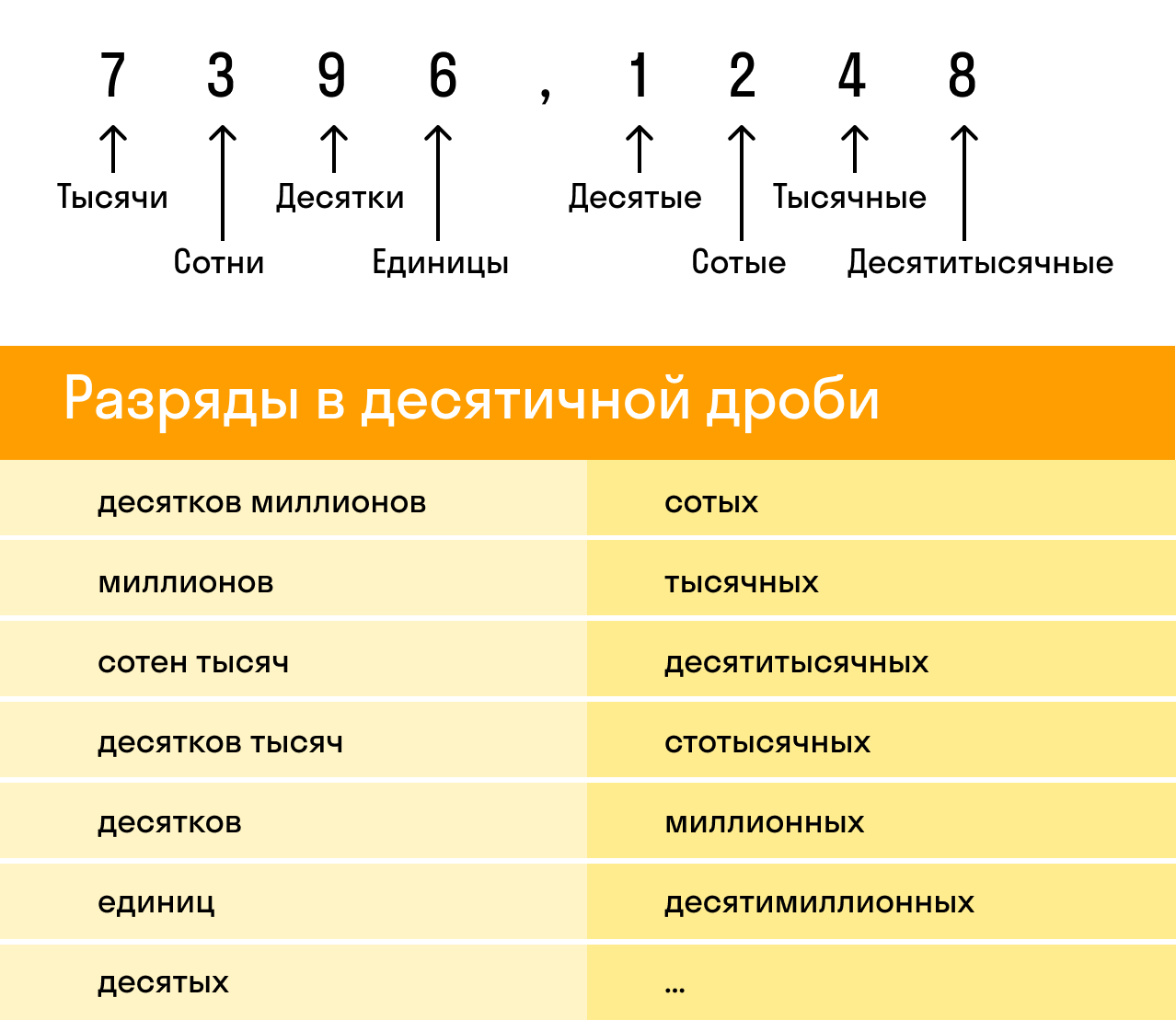
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Правила округления. Обработка и представление результатов измерений. Процедура
Обработка и представление результатов измерений. Процедура
1. Назначение и область применения
1.1. Процедура устанавливает единые требования к обработке и представлению результатов измерений, полученных в лаборатории (центре).
1.2. Представление результатов измерений в лабораторных журналах и в документах, выдаваемых лабораторией, осуществляется согласно методикам измерений и данной процедуре.
1.3. Требования настоящей процедуры распространяются на всех специалистов лаборатории (центра).
2. Нормативные ссылки
2.1. СТ СЭВ 543-77 «Числа. Правила записи и округления» (настоящий стандарт является обязательным в рамках Конвенции о применении стандартов СЭВ);
2.2. ГОСТ 8.736-2011 «Государственная система обеспечения единства измерений (ГСИ). Измерения прямые многократные. Методы обработки результатов измерений. Основные положения»;
2.3. МР 18.1.04-2005 «Система контроля качества результатов анализа проб объектов окружающей среды»;
2.4. ПМГ 96-2009 «Государственная система обеспечения единства измерений (ГСИ). Результаты и характеристики качества измерений. Формы представления» (правила по межгосударственной стандартизации введены в действие для добровольного применения в РФ в качестве рекомендаций по метрологии РФ).
Примеры
1) Число 12,0 – имеет три значащие цифры;
2) Число 30 – имеет две значащие цифры;
3) Число 120 × 10 3 – имеет три значащие цифры;
4) Число 0,514 × 10 – имеет три значащие цифры;
5) Число 0,0056 × 10 – имеет две значащие цифры;
6) Число 0,704 – имеет три значащие цифры;
7) Число 68 – имеет две значащие цифры.
Таким образом, нули вначале числа всегда незначимы; нули в середине числа между ненулевыми цифрами значимы; нули в конце числа могут быть значимыми и незначимыми.
По количеству значащих цифр осуществляется запись приближенных чисел (согласно СТ СЭВ 543-77).
Пример
Следует различать числа 2,4 и 2,40.
Запись 2,4 означает, что верны только цифры целых и десятых; истинное значение числа может быть, например, 2,43 и 2,38.
Запись 2,40 означает, что верны и сотые доли числа; истинное число может быть, например, 2,403 и 2,398, но не 2,421 и не 2,382.
3.2. Округление числа – это отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда (согласно СТ СЭВ 543-77).
В случае, если первая из отбрасываемых цифр (считая слева направо) меньше 5, то последняя сохраняемая цифра не меняется.
В случае, если первая из отбрасываемых цифр (считая слева направо) равна или больше 5, то последняя сохраняемая цифра увеличивается на единицу.
Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление может привести к ошибкам.
Примеры
1) Если число 12,364 требуется округлить до сотых долей, после округления получаем число 12,36; если число 12,364 требуется округлить до десятых долей, после округления получаем число 12,4.
2) Если число 0,703 требуется округлить до сотых долей, получаем число 0,70; если число 0,703 требуется округлить до десятых долей, после округления получаем число 0,7.
3) Если число 0,703 требуется округлить до двух значащих цифр, после округления получаем число 0,70; если число 0,703 требуется округлить до одной значащей цифры, после округления получаем число 0,7.
4) Если число 0,429 требуется округлить до двух значащих цифр, после округления получаем число 0,43; если число 0,429 требуется округлить до одной значащей цифры, после округления получаем число 0,4.
5) Если число 8,574 требуется округлить до двух значащих цифр, после округления получаем число 8,6; если число 8,574 требуется округлить до одной значащей цифры, после округления получаем число 9.
6) Поэтапное округление результата измерения 227,46 дает на первом этапе 227,5 и на втором этапе 228, в то время как правильный результат округления 227.
3.3. Окончательный результат – это результат измерения с погрешностью, который вносится испытателями в лабораторные журналы. Окончательный результат выдается лабораторией в протоколе испытаний.
3.4. Промежуточные результаты – это вся информация по анализу от показания приборов до окончательного результата (в том числе расчеты результатов единичных определений; расчет результата измерения как среднеарифметическое значение результатов единичных определений, полученных в условиях повторяемости; контроль повторяемости; расчет погрешности). Промежуточные результаты заносятся испытателями в лабораторные журналы, но в протоколах испытаний не выдаются.
4.1. Требования к промежуточному результату
4.1.1. Число значащих цифр в промежуточных вычислениях при обработке результатов измерений должно быть больше, чем в окончательном результате.
4.1.2. Если значение погрешности (неопределенности) результата измерений представлено числом, содержащим две значащие цифры, то для промежуточных результатов расчета сохраняем не менее трех значащих цифр.
4.1.3. Если значение погрешности (неопределенности) результата измерений представлено числом, содержащим одну значащую цифру, то для промежуточных результатов расчета сохраняем не менее двух значащих цифр.
4.1.4. При проведении промежуточных расчетов в рукописных лабораторных журналах в числовых значениях измеряемой величины и погрешности следует оставлять столько значащих цифр, чтобы в окончательном результате не появлялась ошибка, связанная с поэтапным округлением.
Примеры
| Промежуточные результаты | Окончательные результаты |
| 0,178 ± 0,053 | 0,18 ± 0,05 |
| 0,1784 ± 0,0533 | 0,178 ± 0,053 |
| 1,22 ± 0,18 | 1,2 ± 0,2 |
| 1,224 ± 0,183 | 1,22 ± 0,18 |
| 3,74 ± 0,748 | 3,7 ± 0,7 |
| 3,742 ± 0,748 | 3,74 ± 0,75 |
| 12,83 ± 1,28 | 12,8 ± 1,3 |
| 54,2 ± 5,4 | 54 ± 5 |
| 54,23 ± 5,42 | 54,2 ± 5,4 |
| 177,6 ± 33,7 | 178 ± 34 |
| 2357,4 ± 212,2 | 2357 ± 212 |
| 11624,8 ± 5812,4 | 11624 ± 5812 |
4.2. Требования к окончательному результату
4.2.1. Числовые значения результата измерений и его погрешности (неопределенности) записываются с указанием одной и той же единицы измерения.
Примеры
(5,4 ± 0,5) мг/дм³;
(6,1 ± 0,7) ммоль/ дм³.
4.2.2. Числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение его погрешности (неопределенности).
Примеры
| Правильно | Неправильно |
| 0,043 ± 0,004 | 0,043 ± 0,0043 |
| 0,0428 ± 0,0043 | 0,0428 ± 0,004 |
| 17,0 ± 0,2 | 17,00 ± 0,2 или 17 ± 0,2 |
| 12,13 ± 0,17 или 12,1 ± 0,2 | 12,1 ± 0,17 или 12,13 ± 0,2 |
| 46,40 ± 4,64 или 46,4 ± 4,6 | 46,402 ± 4,64 или 46,4 ± 4,64 |
4.2.3. Значение погрешности (неопределенности) результата измерений представляют числом, содержащим одну или две значащих цифры. Если числовое значение погрешности (неопределенности) в целой части числа содержит три и более цифр, то результат и погрешность округляются до целых чисел без подсчета количества значащих цифр.
Примеры
| Результаты измерения |
| 0,14 ± 0,05 |
| 0,164 ± 0,051 |
| 1,1 ± 0,1 |
| 1,18 ± 0,11 |
| 3,6 ± 0,6 |
| 3,28 ± 0,54 |
| 12,4 ± 1,2 |
| 44 ± 4 |
| 44,2 ± 4,4 |
| 168 ± 34 |
| 2357 ± 212 |
| 23684 ± 1184 |
4.2.4. Если заказчик требует другие формы представления результатов измерений, лаборатория оставляет за собой право учитывать эти требования.
Ответственность за правильность обработки и представления результатов измерений несут специалисты лаборатории.
Представление результатов измерений на примере определения обобщенных и химических показателей в воде с учетом требований методик измерений
1. Железо общее (ГОСТ 4011-72)
Округлять результат до двух значащих цифр.
Примеры
| Окончательные результаты, мг/дм³ | Промежуточные результаты, мг/дм³ |
| 0,12 ± 0,03 | 0,116 ± 0,029 |
| 0,18 ± 0,04 | 0,178 ± 0,0445* |
| 0,18 ± 0,05 | 0,183 ± 0,046 |
| 0,31 ± 0,08 | 0,308 ± 0,077 |
| 1,3 ± 0,3 | 1,26 ± 0,32 |
| 1,8 ± 0,3 | 1,77 ± 0,32 |
| 12 ± 2 | 12,4 ± 2,2 |
| 25 ± 5 | 25,3 ± 4,6 |
2. Хлориды (ПНД Ф 14.1:2:3.96-97)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения характеристики погрешности.
3. Фосфорсодержащие вещества (ГОСТ 18309-2014)
Числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение характеристики погрешности, выраженное в мг/дм³ и содержащее не более двух значащих цифр.
4. Взвешенные вещества (ПНД Ф 14.1:2:3.110-97)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения характеристики погрешности.
5. Цветность (ГОСТ 31868-2012)
В протоколе указывают метод определения цветности по настоящему стандарту, результат с указанием единиц измерения (например, градусов цветности по хром-кобальтовой шкале Cr-Co) и температуру пробы анализируемой воды.
При определении цветности при постоянной комнатной температуре (20 ± 5) °С в конкретной лаборатории допускается по согласованию с заказчиком не указывать в протоколе значение температуры.
6. Металлы (ПНД Ф 14.1:2:4.139-98)
Примеры записи числовых значений:
| Диапазон, мг/дм³ | Точность округления, мг/дм³ |
| от 0,004 до 0,01 вкл. | 0,0001 |
| от 0,01 до 0,1 вкл. | 0,001 |
| от 0,1 до 1 вкл. | 0,01 |
| от 1 до 10 вкл. | 0,1 |
| свыше 10 | 1 |
7. Алюминий (ГОСТ 18165-2014)
Числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и абсолютное значение характеристики погрешности измерений, выраженное в мг/дм³. Абсолютное значение характеристики погрешности измерений представляют двумя значащими цифрами, если первая цифра не превышает 3. В остальных случаях оставляют одну значащую цифру.
Примеры
| Окончательные результаты, мг/дм³ | Промежуточные результаты, мг/дм³ |
| 0,287 ± 0,057 | 0,2872 ± 0,0574 |
| 0,262 ± 0,052 | 0,2623 ± 0,05246* |
| 2,38 ± 0,48 | 2,381 ± 0,476 |
| 13,5 ± 2,7 | 13,47 ± 2,69 |
| 16,6 ± 3,3 | 16,62 ± 3,32 |
| 22 ± 4 | 21,8 ± 4,4 |
| 27 ± 5 | 27,4 ± 5,48* |
| 38 ± 7 | 38,47* ± 7,7 |
| 51 ± 10 | 51,46* ± 10,3 |
8. Нефтепродукты (ПНД Ф 14.1:2:4.128-98)
Примеры записи числовых значений, мг/дм³:
| 0,009 ± 0,005 | 0,08 ± 0,03 |
| 0,65 ± 0,16 | 3,5 ± 0,9 |
| 3,5 ± 0,9 | 25 ± 6 |
9. Анионные поверхностно-активные вещества (ПНД Ф 14.1:2:4.158-2000)
| Примеры записи для питьевой воды, мг/дм³ | Примеры записи для природной и сточной воды, мг/дм³ |
| 0,028 ± 0,010 | 0,080 ± 0,032 |
| 0,44 ± 0,12 | 0,35 ± 0,11 |
| 4,8 ± 1,0 | 71 ± 17 |
10. Щелочность (МП УВК 1.19-2013)
Численные значения результата количественного химического анализа должны оканчиваться цифрой того же разряда, что и численное значение характеристики погрешности. Характеристику погрешности измерения следует выражать числом, содержащим не более двух значащих цифр.
11. Температура, прозрачность, запах (РД 52.24.496-2018)
Численное значение результата измерений должно оканчиваться цифрой того же разряда, что и значение характеристики погрешности.
12. Кальций (РД 52.24.403-2018)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения погрешности; последние не должны содержать более двух значащих цифр.
13. Перманганатная окисляемость (ПНД Ф 14.1:2:4.154-99)
Результаты измерений округляют с точностью:
| Диапазон, мг/дм³ | Точность округления, мг/дм³ |
| от 0,25 до 1,0 вкл. | 0,01 |
| от 1,0 до 10 вкл. | 0,1 |
| свыше 10 | 1 |
14. Фториды (ПНД Ф 14.1:2:4.270-2012)
Результаты измерений концентрации фторид-ионов при занесении в протокол округляют с точностью:
| Диапазон, мг/дм³ | Точность округления, мг/дм³ |
| от 0,15 до 10 вкл. | 0,01 |
| свыше 10 | 0,1 |
15. Растворенный кислород (ПНД Ф 14.1:2:3.101-97)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения характеристики погрешности.