Однозначное число что это с минусом
0 Однозначное число или нет
Чтобы правильно ответить на этот вопрос необходимо понимать, что такое число, что такое цифра, что такое однозначное число.
Цифра это – знак, который используют для записи числа. Цифр всего десять: 0,1,2,3,4,5,6,7,8,9
Число – это математическое понятие, используемое для описания количества.
Однозначное число – это число, записанное одним знаком.
0 – это и цифра, и число одновременно, но к натуральным числам 0 отнести нельзя, так как натуральные числа – это те, которые используются при счёте предметов.
Если в вопросе речь идёт о натуральных числах, то самое маленькое однозначное число 1.
Математика – наука точная и двусмысленные ответы на одни и те же вопросы, касающиеся чисел, представить сложно, но все же есть определенные исключения. Какое самое маленькое однозначное число: 0 или 1 и на что стоит опираться, давая верный ответ?
Принято считать, что самое маленькое однозначное число – это ноль. Но специалисты в области математики уверяют, что в этом вопросе не все так однозначно. Чтобы понять, какое число является самым маленьким, необходимо разобраться в специфике числового ряда.
Для удобства подсчета в математике принята система цифр и чисел. Цифра – это знак от 0 до 9. Числа складываются из цифр. Они бывают однозначные, двузначные, трехзначные и так далее. Однозначные числа состоят из одной цифры. Иными словами, они представляют собой первое число первого разряда класса единиц. Человеку, далекому от математики, может показаться такое описание достаточно сложным. Но на самом деле оно было придумано для упрощения подсчетов. При помощи разложения любого числа на разряды и классы можно быстро освоить счет, не пользуясь калькулятором. Элементарные знания математики необходимы как школьникам, так и взрослым людям. Конечно, не все специалисты используют в своей деятельности или повседневной жизни то, что было освоено во время изучения школьной программы. Но элементарное незнание числового ряда указывает на неграмотность. Математика – это язык, при помощи которого у человека появляется возможность осваивать другие точные науки. Без получения определенных знаний невозможно изучение физики, информатики и других дисциплин.
Какое самое маленькое число принято считать в математике однозначным? Если речь идет о полном числовом ряде, то самое маленькое число – это ноль. Его еще называют границей между отрицательным и положительным рядом. Ноль – это отсутствие предмета. Но на этот счет у ученых существует два мнения. В математике принято выделять числа натуральные. Они возникают естественным образом при подсчете. Последовательность натуральных чисел, расположенных в порядке возрастания, называется натуральным рядом. Самое маленькое натуральное число – единица. Именно с нее начинается счет. Когда человек видит перед собой несколько предметов, отсчет ведется не от 0, а от 1. Это совершенно логично и понятно.
Ряд однозначных чисел заканчивается девяткой. Именно 9 считается самым большим однозначным числом в ряду. Самое маленькое двузначное число – 10. Оно открывает разряд десятков. Важно понимать, что цифра в каждом последующем числовом ряду на порядок более значима, чем та, которая стоит в ряду предыдущем. Например единица десятков ровно в 10 раз больше единицы, принадлежащей к разряду единиц.
Почему ноль не входит в ряд натуральных чисел? Ответ очень прост. Ноль – это отсутствие чего либо. С него невозможно начать счет. Многие ученые считают, что 0 никак нельзя считать наименьшим числом, так как есть еще и числа отрицательного ряда. Таким образом, говорить о наименьшем числе невозможно. До сих пор не названы максимальное число в положительном числовом ряду и минимальное – в отрицательном. Ограничения можно установить только по классам. Для удобства подсчета в математике принято выделять классы единиц, тысяч, миллионов, триллионов и так далее. Самое маленькое число в классе тысяч, например, – 1000, а самое большое – 999 000. Для разложения любого числа в ряд не нужны специфические знания. Сделать это достаточно просто, если использовать специальные таблицы или он-лайн сервисы.
Самое маленькое однозначное число – это ноль. Но такой вариант ответа актуален только если речь идет обо всем положительном числовом ряде. Самое маленькое натуральное число в ряду – единица. Именно с него начинается предметный отсчет.
Наименьшее однозначное число
Автор Ўлия Михайловская задал вопрос в разделе Домашние задания
Почему наименьшим однозначным числом является 1, а не 0? и получил лучший ответ
По горизонтали: 1. Единица длины. 2. Фамилия древнегреческого математика. 3.
подробнее.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Вычитание натуральных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Мы можем не только собирать в группы различные предметы, то есть, складывать их, но и забирать из существующей группы определенное их количество.
Разность (или остаток) – это такое число, которое получится, если от одного числа отнять другое, то есть, от всех единиц одного числа отнять все единицы, которые содержатся в другом числе.
Уменьшаемое – это то число, от которого мы отнимаем единицы другого числа.
Вычитаемое – это число, которое мы вычитаем из другого числа. То есть, то число, на количество единиц которого мы уменьшаем другое число.
Вычитание – это арифметическое действие, которое выполняется для получения разности двух или нескольких чисел.
то есть, совершить действие вычитания – это найти такое число, которое получится, если от данного числа отнять определенное количество единиц другого числа.
Совершая вычитание натуральных чисел, вы должны помнить, что из одного натурального числа можно вычесть только равное ему или меньшее натуральное число. Действительно, мы никак не можем отобрать единиц предметов больше, чем их есть в наличии.
Связь вычитания и сложения
Действительно, когда мы ищем сумму, мы складываем все единицы, из которых состоят числа, вместе. То есть, получаем число, которое складывается из разных чисел.
Поэтому, вычитание и сложение – это взаимно обратные действия. Если нам известна сумма двух слагаемых, мы можем превратить ее в разность двух чисел, и наоборот, разность можно перевести в сумму.
Свойства разности натуральных чисел
Свойства разности натуральных чисел состоят из:
Рассмотрим каждый пункт подробнее.
Правила вычитания суммы из числа и числа из суммы
Как вычесть сумму из числа
Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.
То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.
Рассмотрим это на примере из урока сложение чисел.
325 +( 12 + 64 + 5 ) = 325 +81 = 406
Я запишу это в виде разности:
и покажу, что результат будет равен первому слагаемому:
Как видите, все верно.
Как вычесть число из суммы
Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.
То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.
Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.
Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:
325 +81 = ( 191 + 65 + 150 )
Превращаю выражение в разность:
( 191 + 65 + 150 )-81 = 325
и покажу, что результат также будет равен первому слагаемому:
Как меняется разность при изменении вычитаемого или уменьшаемого
Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.
Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.
Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.
Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.
Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.
Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.
Правила вычитания разности
Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:
1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;
2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.
Это свойство выводится из предыдущих, рассмотренных нами.
22 — 17 = 5
5+ 3 = 8
22 +3-( 17 +3- 3 )
25- 17 +0 = 8
Как видите, оба способа показали верный результат.
Вычитание однозначного числа
Вычитание в столбик многозначных чисел
Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.
После нахождения разности чисел способом вычитания в столбик записываем ответ в строчном примере:
50063-4825 = 45238.
Как проверить действия сложение и вычитание?
Проверить сложение можно двумя способами: обратным сложением и вычитанием.
Обратное сложение означает, что мы меняем слагаемые местами, и складываем их еще раз. Если результат будет такой же, как и после первого сложения, значит, вычисление было верным.
Проверка сложения вычитанием – это способ, при котором нужно из суммы, которую получили после выполнения действия сложение, отнять одно из слагаемых. Если результат этого вычитания будет равен второму слагаемому (или сумме остальных слагаемых, если их больше двух), значит сложение было выполнено верно.
И этот способ проверки показал правильность нашего решения.
Проверить вычитание также возможно и сложением, и другим вычитанием.
Проверка вычитания сложением основана на взаимосвязи вычитания и сложения. Зная, что уменьшаемое – это сумма, а остаток и вычитаемое – это слагаемые, мы можем сложить между собой вычитаемое и остаток, и, если получим в результате уменьшаемое, значит, мы правильно сделали действие.
Вот так выглядит проверка вычитания сложением на примере вычисленной на этом уроке разницы 50063-4825 = 45238 :
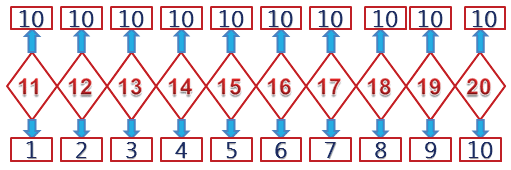
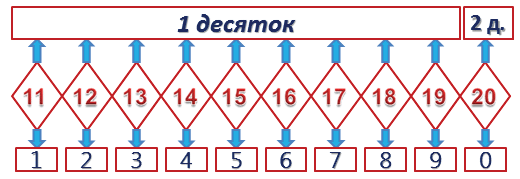
Числа от 1 до 100. Состав числа. Круглые числа
Числа от 1 до 100
Предыдущее и последующее число
56 , 57
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Состав двузначного числа
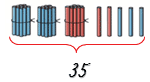
Всего на рисунке 35 палочкек.
35 = 30 + 5
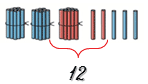
Красных палочек 12.
12 = 10 + 2
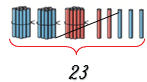
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
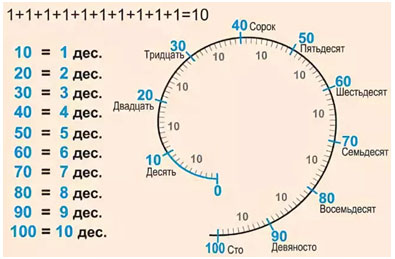
Круглые числа
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
10 + 40 = 50
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:
Действия с десятками и единицами
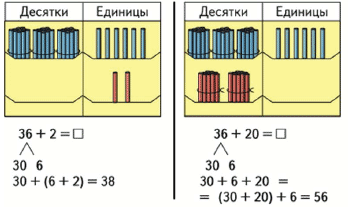
Как решить пример 34 + 25?
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
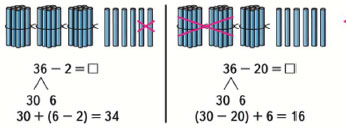
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях: