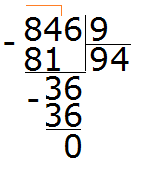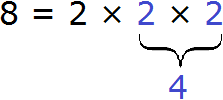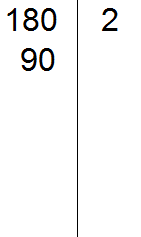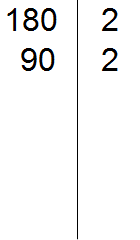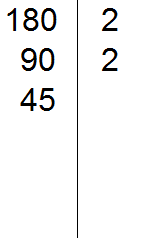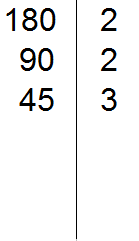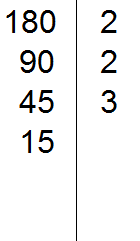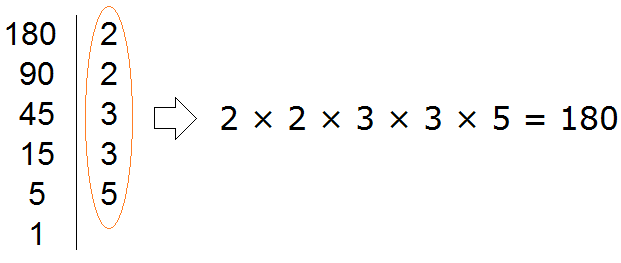Однократное число что такое
Значение слова «однократный»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ОДНОКРА’ТНЫЙ, ая, ое (книжн.). Бывший, происшедший, сделанный один раз. ◊
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
однокра́тный
1. бывший, свершившийся, совершенный лишь один раз ◆ При однократном и малоцикловом нагружениях в условиях комнатных температур используются плоские образцы с симметричными центральными или боковыми трещинами. А.Н. Романов, «Разрушение при малоцикловом нагружении», 1988 г.
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова трёхчленный (прилагательное):
Синонимы к слову «однократный»
Предложения со словом «однократный»
Цитаты из русской классики со словом «однократный»
Сочетаемость слова «однократный»
Что (кто) бывает «однократным»
Понятия, связанные со словом «однократный»
Отправить комментарий
Дополнительно
Предложения со словом «однократный»
Разработан и такой антибиотик, однократный приём которого внутрь обеспечивает курсовое лечение.
Эти штуковины имели однократное применение – после загрузки носитель разрушался.
Создание видения – для вашей организации или её отдела, для вашей работы и для вашей жизни – это путь, а не однократное действие.
Однократное число что такое
однократный — однократный … Орфографический словарь-справочник
однократный — единовременный, одноразовый Словарь русских синонимов. однократный см. единовременный Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова … Словарь синонимов
ОДНОКРАТНЫЙ — ОДНОКРАТНЫЙ, ая, ое; тен, тна. Происшедший или сделанный один раз. Однократное посещение. • Однократный глагол в грамматике: глагол, называющий действие, совершаемое мгновенно, напр. моргнуть, стукнуть. | сущ. однократность, и, жен. Толковый… … Толковый словарь Ожегова
однократный — одинарный единый — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4404] Тематики защита информации Синонимы одинарныйединый EN single … Справочник технического переводчика
Однократный — прил. Бывший, свершившийся, совершенный лишь один раз. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
однократный — однократный, однократная, однократное, однократные, однократного, однократной, однократного, однократных, однократному, однократной, однократному, однократным, однократный, однократную, однократное, однократные, однократного, однократную,… … Формы слов
однократный — однокр атный; кратк. форма тен, тна … Русский орфографический словарь
однократный — … Орфографический словарь русского языка
однократный — однокра/тный … Слитно. Раздельно. Через дефис.
однократный — Syn: см. единовременный … Тезаурус русской деловой лексики
Однократный
(Слово «Однократный» может использоваться сокращённо в тексте как «О.» или «о.»)
Однократный — как пишется слово, постановка ударения
правописание или как правильно написать слово, ударные и безударные гласные в нем, различные формы слова «Однократный»
Толковый словарь русского языка. Д.Н. Ушаков
однократная, однократное (книжн.). Бывший, происшедший сделанный один раз. Однократный вид (грам.) — форма глагола, обозначающая, что действие совершилось или совершится в один прием, мгновенно, напр.: скакнуть, кольнуть, ущипнуть.
Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
прил. Бывший, свершившийся, совершенный лишь один раз.
Примеры употребления слова однократный в литературе.
Чудесным избавлением, прокладывающим себе дорогу в пространствующий мир высших сфер, сжимающихся и мерно расширяющихся в такт ритмической сущности того нелегкого, но таинственного пространства в просветах пещер которого, занавешивающих себя сталактитами и сталагмитами, покоящихся, вечно-сущих, самососредоточенных, оснований самой музыки, развертывание которого образует легкие всякого легкого дыхания, прокалывамые лишь только склеванными ребрами музыкальных оснований композиторского скелета, обновляющегося меловой известью так и не извевшихся до музыкальных оснований вод бассейна, возникающего в подражание священному одиночеству мысли призрака, отведывающего горьковатую настойку совести в целях риторического прокашливания с привкусом времени и рябиновых ягод, которые гроздьями поглощаются в том неистовом невыносимом упорстве, уносящемся от себя самого, упускающего себя самого через певчую прорезь сознания, упрямства мышления, желающего возбудить вкус в отпавших от бытия вещах в качестве такого их внутреннего с
Через неделю пришло согласие Комиссии по вопросам медицинской этики на однократное проведение испытания препарата РОМ-55 на пациенте Конраде Ланге, шестидесяти семи лет.
При острой лучевой болезни легкой степени у некоторых больных могут отсутствовать признаки первичной реакции, но у большинства через несколько часов наблюдается тошнота, возможна однократная рвота.
При этом, в зависимости от состояния больного, можно ограничиться однократной или двукратной инъекцией, а далее назначать прием внутрь, как указано ранее.
Учитывая вышеприведенные аргументы, не можем поддержать Вашу позицию о противоречии этого подхода принципу однократного налогообложения, установленному ст.
Однократного анализа недостаточно, так как скрытый период болезней, передаваемых половым путем, может составлять от 2-3 дней до нескольких месяцев.
Под влиянием лечения пятна исчезаютчерез 10-12 дней, но однократный курс лечения, как правило, является недостаточным.
Если слегка зажмуриться и сделать мельчайший шаг, пусть однократный, если устремиться сквозь не столь уж плотную занавеску времени, то.
Ибо однократный арест функционеров не означает конца движения, но дело идет всегда от одного ареста к другому.
Чистый препарат предохраняет от укусов комаров в течение 6 часов, для однократного смазывания лица, шеи, рук достаточно 15-20 капель.
Описываю этот способ однократного догона глиссады, только чтобы показать: самолет охотно теряет высоту, не успевая разогнать поступательную скорость, но требует значительных усилий, чтобы потом уменьшить снижение, а значит, осмысленных, упреждающих действий капитана.
Факт есть нечто однократное, это то, что было или будет в действительности.
А у меня имелось разрешение только на однократное пересечение границы.
В частности, это позволяет после однократной разметки быстро находить нужный фрагмент текста.
И опять учнут ловить свата и пороть соломенным кнутом, опять будет озорное веселье, многократное для языка русского и однократное, единое в жизни для каждого из племени русичей, зато и запоминаемое на всю жизнь.
Источник: библиотека Максима Мошкова
Транслитерация: odnokratnyiy
Задом наперед читается как: йынтаркондо
Однократный состоит из 11 букв
Что такое кратное число
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.
Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.
Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.
Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.
Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).
А у чисел, которые участвуют в делении, есть определенные названия:
Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.
Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.
Одно число называется кратным другому, если его можно на него поделить без остатка.
Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6
Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.
Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:
Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.
Таблицы чисел кратных 2,3,4,5,6,7,9
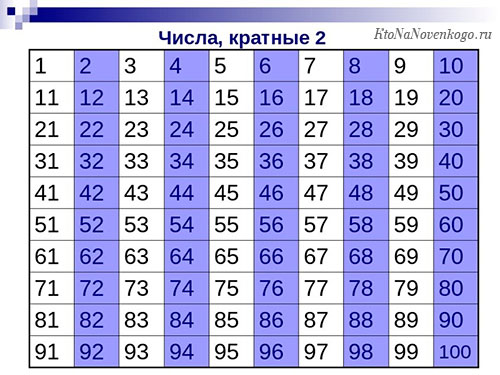
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.
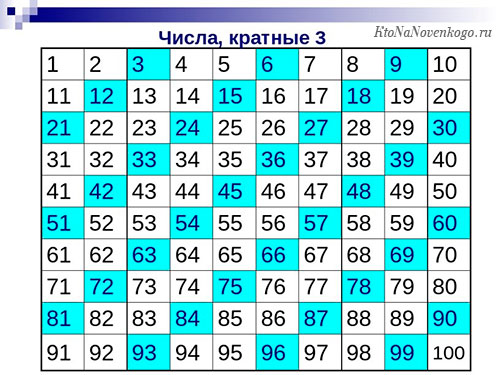
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.
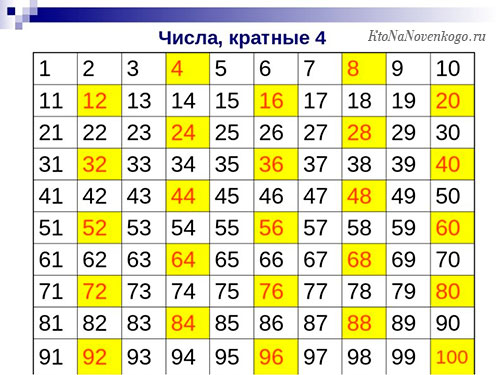
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.
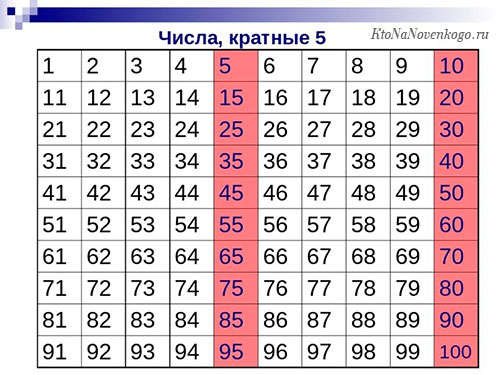
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.
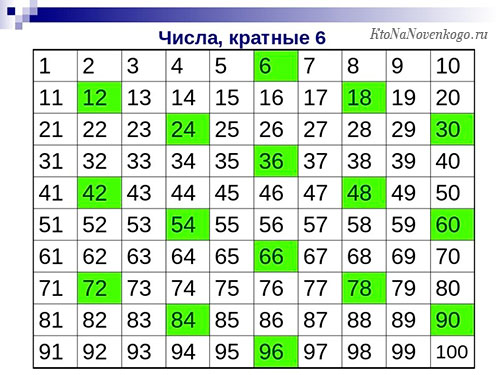
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.
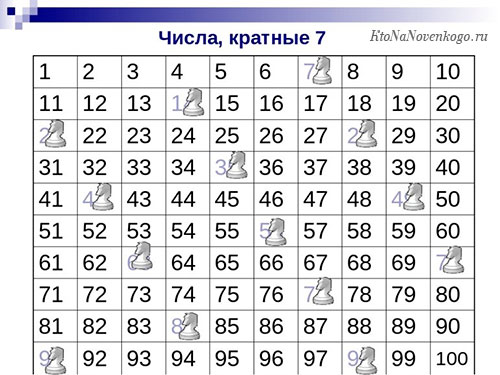
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».
И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.
Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.
| Числа, кратные 9 | 27 | 198 | 5 877 | 3 816 | 117 | 72 |
|---|---|---|---|---|---|---|
| Сумма | 9 | 18 | 27 | 18 | 9 | 9 |
Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.
Вместо заключения
А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.
Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.
Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.
Делитель и кратное в математике
Что такое делители и кратные числа
Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.
Выделяют следующие компоненты деления:
Делимое — число, которое делят на несколько частей.
Делитель — число, которое показывает, на сколько частей нужно разделить делимое.
Частное — число, которое является результатом деления.
Умножение частного на делитель дает делимое.
Чтобы получить делитель, нужно делимое разделить на частное.
Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е
Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.
16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.
Делителем числа a называется такое число b, на которое a делится нацело.
Например, 9 : 4 = 2 (остаток 5 ).
В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.
Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.
Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.
Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.
Тогда представим решение данной задачи в виде уравнения:
72 — целое число, без остатка.
Произведение делителей должно дать в результате 144:
72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.
Ответ: числа 2 и 72 — делители 144.
Число называют кратным, если оно делится на данное число нацело, без остатка.
Например, 15:3 нацело.
Тогда число 15 является кратным 3.
Слово «кратно» синонимично слову «делится».
Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».
Основные понятия и определения
Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.
Делится нацело = без остатка.
Наименьшим делителем любого числа является единица.
Наибольшим делителем числа является само число.
Делителем нуля будет любое число, но сам 0 делителем не будет.
При делении нуля на любое число получаем 0. А делить на ноль нельзя.
У единицы только один делитель — единица.
Другие числа, кроме 1, имеют не меньше двух делителей.
Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.
Наименьшее кратное числа является равным самому числу.
Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.
Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.
Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Примеры решения задач
Необходимо найти делители числа 14.
Решить задание можно двумя способами.
Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.
Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.
Ответ: делители числа 14: 1, 2, 7, 14.
Представим 14 в виде произведения чисел:
Делителями будут множители, так как можем разделить 14 нацело на каждый из них.
Ответ: делители 14: 1, 2, 7, 14.
Найдите три числа, кратных 7.
Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.
7 * 1 = 7 — семь кратно семи;
7 * 2 = 14 — 14 кратно 7;
7 * 3 = 21 — 21 кратно 7.
Ответ: числа, кратные 7: 7, 14, 21.
Самостоятельно проверьте, 225 кратно 3 или нет.
Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.
75 — целое число, при делении нет остатка. Тогда 225 кратно 3.
Найдите любое число, делителями которого являются числа 7 и 8.
Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:
Делители и кратные
В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
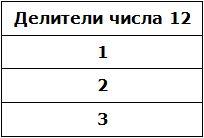
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
Определение. Кратным числа а называется число, которое делится без остатка на а.
Кратным числа 5 называется число, которое делится без остатка на 5 .
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
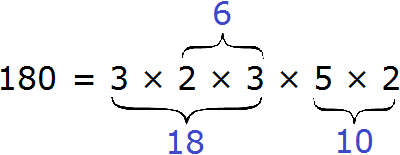
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
Теперь раскладываем множители 18 и 10 на другие множители:
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
Теперь собираем все простые множители вместе:
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
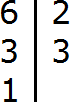
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
Например, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180
Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
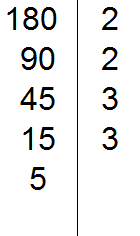
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
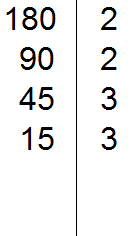
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
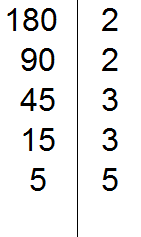
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
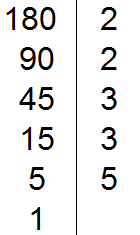
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1
Теперь раскладываем число 12 на простые множители:
Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
Занесём число 4 в нашу таблицу делителей
Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:
Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:
Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
Теперь разложим число 6 на простые множители:
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
1, 2, 3, 6