Один децибел равен чему
Что такое децибел (дБ)?
Определение децибел (дБ), как преобразовать, калькулятор и таблица соотношения дБ.
Децибел (дБ) определение
Децибел используется для обозначения уровня акустических волн и электронных сигналов.
Логарифмическая шкала может описывать очень большие или очень маленькие числа в более коротких обозначениях.
Уровень дБ можно рассматривать как относительное усиление одного уровня по сравнению с другим уровнем или как уровень абсолютной логарифмической шкалы для хорошо известных опорных уровней.
Отношение в белах представляет собой десятичный логарифм отношения P 1 и P 0 :
Децибел равен одной десятой бела, поэтому 1 бел равен 10 децибелам:
Коэффициент мощности
Отношение мощностей в децибелах (дБ) равно десятикратному логарифму по основанию 10 отношения P 1 и P 0 :
Соотношение амплитуд
Соотношение таких величин, как напряжение, сила тока и уровень звукового давления, рассчитывается как отношение квадратов.
Отношение амплитуд в децибелах (дБ) составляет 20 логарифмов по основанию 10 отношения V 1 и V 0 :
Калькулятор преобразования децибел в ватты, вольты, герцы, паскаль
Преобразование дБ, дБм, дБВт, дБВ, дБмВ, дБмкВ, дБу, дБмкА, дБГц, дБУЗД, дБА в ватты, вольты, амперы, герцы, звуковое давление.
Отношение мощности к преобразованию дБ
пример
Найдите коэффициент усиления в дБ для системы с входной мощностью 5 Вт и выходной мощностью 10 Вт.
преобразование отношения дБ к мощности
Отношение амплитуды к преобразованию дБ
Для амплитуды волн, таких как напряжение, ток и уровень звукового давления:
1 является ссылка амплитуды уровня.
преобразование отношения дБ к амплитуде
1 является ссылка амплитуды уровня.
пример
Найдите выходное напряжение для системы с входным напряжением 5 В и усилением по напряжению 6 дБ.
Усиление напряжения
Коэффициент усиления по напряжению ( G дБ ) равен 20 логарифму по основанию 10 отношения выходного напряжения ( V out ) и входного напряжения ( V in ):
Текущая прибыль
Коэффициент усиления по току ( G дБ ) равен 20 логарифму по основанию 10 отношения выходного тока ( I out ) и входного тока ( I in ):
Акустическое усиление
Акустическое усиление слухового аппарата ( G дБ ) в 20 раз превышает логарифм по основанию 10 отношения выходного уровня звука ( L out ) и входного уровня звука ( L in ).
Отношение сигнал / шум (SNR)
Отношение сигнал / шум ( SNR дБ ) в 20 раз превышает логарифм по основанию 10 амплитуды сигнала ( сигнал A ) и амплитуды шума ( шум A ):
Абсолютные единицы децибел
Абсолютные единицы децибел относятся к определенной величине единицы измерения:
| Ед. изм | название | Справка | Количество | Соотношение |
|---|---|---|---|---|
| дБм | децибел милливатт | 1 мВт | электроэнергия | коэффициент мощности |
| дБВт | децибел ватт | 1Вт | электроэнергия | коэффициент мощности |
| дБн | опорный шум в децибелах | 1пВт | электроэнергия | коэффициент мощности |
| дБмкВ | децибел микровольт | 1 мкВ RMS | вольтаж | соотношение амплитуд |
| дБмВ | децибел милливольт | 1 мВ RMS | вольтаж | соотношение амплитуд |
| дБВ | децибел вольт | 1 В RMS | вольтаж | соотношение амплитуд |
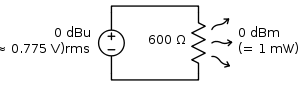
| дБу | децибел без нагрузки | 0,775 В RMS | вольтаж | соотношение амплитуд |
| dBZ | децибел Z | 1 мкм 3 | отражательная способность | соотношение амплитуд |
| дБмкА | децибел микроампер | 1 мкА | текущий | соотношение амплитуд |
| дБом | децибел Ом | 1Ω | сопротивление | соотношение амплитуд |
| дБГц | децибел герц | 1 Гц | частота | коэффициент мощности |
| дБSPL | уровень звукового давления в децибелах | 20 мкПа | звуковое давление | соотношение амплитуд |
| дБА | децибел A-взвешенный | 20 мкПа | звуковое давление | соотношение амплитуд |
Относительные единицы децибел
| Ед. изм | название | Справка | Количество | Соотношение |
|---|---|---|---|---|
| дБ | децибел | — | — | мощность / поле |
| дБн | носитель децибел | мощность несущей | электроэнергия | коэффициент мощности |
| дБи | децибел изотропный | плотность мощности изотропной антенны | удельная мощность | коэффициент мощности |
| дБFS | полная шкала децибел | полная цифровая шкала | вольтаж | соотношение амплитуд |
| дБн | опорный шум в децибелах |
Измеритель уровня звука
Измеритель SPL используется для тестирования и измерения громкости звуковых волн и для мониторинга шумового загрязнения.
Единицей измерения уровня звукового давления является паскаль (Па), а в логарифмической шкале используется дБ-SPL.
Таблица дБ-SPL
Таблица общих уровней звукового давления в дБSPL:
Децибел
Децибе́л — логарифмическая единица уровней, затуханий и усилений. [1]
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять:
где AdB — величина в децибелах, A — измеренная физическая величина, A0 — величина, принятая за базис.
Децибел — это безразмерная единица, применяемая для измерения отношения некоторых величин — «энергетических» (мощности, энергии, плотности потока мощности и т. п.) или «силовых» (силы тока, напряжения и т. п.). Иными словами, децибел — это относительная величина. Не абсолютная, как, например, ватт или вольт, а такая же относительная, как кратность («трёхкратное отличие») или проценты, предназначенная для измерения отношения («соотношения уровней») двух других величин, причём к полученному отношению применяется логарифмический масштаб.
Русское обозначение единицы «децибел» — «дБ», международное — «dB» [2] (неправильно: дб, Дб).
Децибел не является официальной единицей в системе единиц СИ, хотя по решению Генеральной конференции по мерам и весам допускается его применение без ограничений совместно с СИ, а Международное бюро мер и весов рекомендовала включить его в эту систему.
Содержание
Сравнение с другими логарифмическими единицами
| название | сокращение | соответствует изменению в … раз | пересчёт в … | |||
|---|---|---|---|---|---|---|
| дБ | Б | Нп | X m | |||
| децибел | дБ, dB | ≈1,26 ( ) ) | 1 | 0,1 | ≈0,115 | −0,25 |
| бел | Б, B | 10 | 10 | 1 | ≈1,15 | −2,5 |
| непер | Нп, Np | ≈2,72 (e) | ≈8,686 | ≈0,8686 | 1 | ≈−1,086 |
| звёздная величина | X m | ≈0,398 ( ) ) | −4 | −0,4 | ≈−0,921 | 1 |
Области применения
Децибелы широко применяются в любых областях техники, где требуется измерение величин, меняющихся в широком диапазоне: в радиотехнике, антенной технике, в системах передачи информации, в оптике, акустике (в децибелах измеряется уровень громкости звука) и др. Так, в децибелах принято измерять динамический диапазон (например, диапазон громкости звучания музыкального инструмента), затухание волны при распространении в поглощающей среде, коэффициент усиления и коэффициент шума усилителя.
Децибелы используются не только для измерения отношения физических величин второго порядка (энергетических: мощность, энергия) и первого порядка (напряжение, сила тока). В децибелах можно измерять отношения любых физических величин, а также использовать децибелы для представления абсолютных величин (см. опорный уровень).
Переход к децибелам
Любые операции с децибелами упрощаются, если руководствоваться правилом: величина в дБ — это 10 десятичных логарифмов отношения двух одноименных энергетических величин. Всё остальное — следствия этого правила. «Энергетические» — величины второго порядка (энергия, мощность). По отношению к ним напряжение и сила электрического тока («неэнергетические») — величины первого порядка (P
U²), которые должны быть на каком-то этапе вычислений корректно преобразованы в энергетические. [источник не указан 153 дня]
Измерение «энергетических» величин
Изначально дБ использовался для оценки отношения мощностей, и в каноническом, привычном смысле величина, выраженная в дБ, предполагает логарифм отношения двух мощностей и вычисляется по формуле:

Соответственно, переход от дБ к отношению мощностей осуществляется по формуле:


Измерение «неэнергетических» величин
Из правила (см. выше) следует, что «неэнергетические» величины должны быть преобразованы в энергетические. Так, согласно закону Джоуля-Ленца 


В общем случае напряжения U1 и U0 могут регистрироваться на различных по величине сопротивлениях (R1 не равно R0). Такое может быть, например, при определении коэффициента усиления усилителя, имеющего различные выходное и входное сопротивления, или при измерении потерь в согласующем устройстве, трансформирующем сопротивления. Поэтому в общем случае
величина в децибелах = 
Только в частном (весьма распространенном) случае, если оба напряжения U1 и U0 измерялись на одном и том же сопротивлении (R1 = R0), можно пользоваться кратким выражением
величина в децибелах = 
Децибелы «по мощности», «по напряжению» и «по току»
Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R1 = R0 (в частности, если R1 и R0 — одно и то же сопротивление, или в случае, если соотношение сопротивлений R1 и R0 по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:
дБ по напряжению = 

Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует чётко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R1 не равно R0, следует пользоваться выражением для общего случая (см. выше).
Нетрудно подсчитать, что, в частности:
Примеры вычислений
Переход к дБ
Пусть значение мощности P1 стало в 2 раза больше исходного значения мощности P0, тогда
10 lg(P1/P0) = 10 lg(2) ≈3,0103 дБ ≈ 3 дБ,
то есть рост мощности на 3 дБ означает её увеличение в 2 раза.
Пусть значение мощности P1 стало в 2 раза меньше исходного значения мощности P0, то есть P1 = 0,5 P0. Тогда
то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:
Переход от дБ к «разам»
Изменение «в разах» по известному изменению в дБ (условное обозначение «dB» в формулах ниже) вычисляется следующим образом:
Переход от дБ к мощности
Для этого нужно знать значение опорного уровня мощности P0. Например, при P0 = 1 мВт и известном изменении на +20 дБ:

Переход от дБ к напряжению (току)
Для этого нужно знать значение опорного уровня напряжения U0 и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R0 = R1, заданном U0 = 2 В и приросте напряжения на 6 дБ:

Рекомендации
Операции с децибелами можно выполнять в уме: вместо умножения, деления, возведения в степень и извлечения корня применяется сложение и вычитание децибельных единиц. Для этого можно использовать таблицы соотношений (первые 2 — приближённые):
1 дБ → в 1,25 раза, 3 дБ → в 2 раза, 10 дБ → в 10 раз.
Отсюда, раскладывая «более сложные значения» на «составные», получаем:
6 дБ = 3 дБ + 3 дБ → в 2·2 = в 4 раза, 9 дБ = 3 дБ + 3 дБ + 3 дБ → в 2·2·2 = в 8 раз, 12 дБ = 4 · (3 дБ) → в 2 4 = в 16 раз
13 дБ = 10 дБ + 3 дБ → в 10·2 = в 20 раз, 20 дБ = 10 дБ + 10 дБ → в 10·10 = в 100 раз, 30 дБ = 3 · (10 дБ) → в 10³ = в 1000 раз
Сложению (вычитанию) значений в дБ соответствует умножение (деление) самих отношений. Отрицательные значения дБ соответствуют обратным отношениям. Например:
Причины использования децибелов
Для применения децибелов и оперирования логарифмами вместо процентов или долей есть ряд причин:
Условные обозначения
Для различных физических величин одному и тому же числовому значению, выраженному в децибелах, могут соответствовать разные уровни сигналов (вернее разности уровней). Поэтому во избежание путаницы такие «конкретизированные» единицы измерения обозначают теми же буквами «дБ», но с добавлением индекса — общепринятого обозначения измеряемой физической величины. Например дБВ (децибел относительно вольта) или дБмкВ (децибел относительно микровольта), дБВт (децибел относительно ватта) и т. п. В соответствии с международным стандартом МЭК 27-3 при необходимости указать исходную величину её значение помещают в скобках за обозначением логарифмической величины, например, для уровня звукового давления: LP (re 20 µPA) = 20 dB; LP (исх. 20 мкПа) = 20 дБ
Опорный уровень
Децибел служит для определения отношения двух величин. Но нет ничего удивительного в том, что децибел используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень (условный 0 дБ).
Строго говоря, должно быть однозначно определено, какая именно физическая величина и какое именно её значение используются в качестве опорного уровня. Опорный уровень указывается в виде добавки, следующей за символами «дБ» (например, дБм), либо опорный уровень должен быть ясен из контекста (например, «дБ относительно 1 мВт»).
На практике распространены следующие опорные уровни и специальные обозначения для них:
По аналогии образуются составные единицы измерений. Например, уровень спектральной плотности мощности дБВт/Гц — «децибельный» аналог единицы измерения Вт/Гц (мощность, выделяющаяся на номинальной нагрузке в полосе частот шириной в 1 Гц с центром на указанной частоте). Опорным уровнем в данном примере является 1 Вт/Гц, то есть физическая величина «спектральная плотность мощности», её размерность «Вт/Гц» и значение «1». Так, запись «-120 дБВт/Гц» полностью эквивалентна записи «10 −12 Вт/Гц».
В случае затруднения во избежание путаницы достаточно указать опорный уровень явно. Например, запись −20 дБ (относительно 0,775 B на нагрузке 50 Ом) исключает двойное толкование.
Справедливы следующие правила (следствие правил действий с размерными величинами):
При пересчёте уровней мощностей (дБВт, дБм) в уровни напряжений (дБВ, дБмкВ) и обратно необходимо учитывать сопротивление, на котором определяется мощность и напряжение:
Что такое децибел?
Перевод из децибел в разы и обратно
Довольно часто в популярной радиотехнической литературе, в описании электронных схем употребляется единица измерения – децибел (дБ или dB).
При изучении электроники начинающий радиолюбитель привык к таким абсолютным единицам измерения как Ампер (сила тока), Вольт (напряжение и ЭДС), Ом (электрическое сопротивление) и многим другим, с помощью которых обозначают количественно тот или иной электрический параметр (ёмкость, индуктивность, частоту).
Начинающему радиолюбителю, как правило, не составляет особого труда разобраться, что такое ампер или вольт. Тут всё понятно, есть электрический параметр или величина, которую нужно измерить. Есть начальный уровень отсчёта, который принимается по умолчанию в формулировке данной единицы измерения. Есть условное обозначение этого параметра или величины (A, V). И вправду, как только мы читаем надпись 12 V, то мы понимаем, что речь идёт о напряжении, аналогичном, например, напряжению автомобильной аккумуляторной батареи.
Но как только встречается надпись, к примеру: напряжение повысилось на 3 дБ или мощность сигнала составляет 10 дБм (10 dBm), то у многих возникает недоумение. Как это? Почему упоминается напряжение или мощность, а значение указывается в каких-то децибелах?
Практика показывает, что не многие начинающие радиолюбители понимают, что же такое децибел. Попытаемся развеять непроглядный туман над такой таинственной единицей измерения как децибел.
Что такое децибел?
Единицу измерения под названием Бел стали впервые применять инженеры телефонной лаборатории Белла. Децибел является десятой частью Бела (1 децибел = 0,1 Бел). На практике широко используется как раз децибел.
Как уже говорилось, децибел, это особенная единица измерения. Стоит отметить, что децибел не является частью официальной системы единиц СИ. Но, несмотря на это, децибел получил признание и занял прочное место наряду с другими единицами измерения.
Вспомните, когда мы хотим объяснить какое-либо изменение, мы говорим, что, например, стало ярче в 2 раза. Или, например, напряжение упало в 10 раз. При этом мы устанавливаем определённый порог отсчёта, относительно которого и произошло изменение в 10 или 2 раза. С помощью децибел также измеряют эти “разы”, только в логарифмическом масштабе.

График логарифмической зависимости
Например, изменение на 1 дБ, соответствует изменению энергетической величины в 1,26 раза. Изменение на 3 дБ соответствует изменению энергетической величины в 2 раза.
Но зачем так заморачиваться с децибелами, если отношения можно измерять в разах? На этот вопрос нет однозначного ответа. Но уж, поскольку, децибелы активно применяются, то наверняка это оправдано.
Причины для использования децибел всё-таки есть. Перечислим их.


График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера
Так, например, чувствительность человеческого уха уменьшается с ростом уровня громкости звукового сигнала. Именно поэтому, при выборе переменного резистора, который планируется применить в регуляторе громкости звукового усилителя стоит брать с показательной зависимостью сопротивления от угла поворота ручки регулятора. В этом случае, при повороте движка регулятора громкости звук в динамике будет нарастать плавно. Регулировка громкости будет линейной, так как показательная зависимость регулятора громкости компенсирует логарифмическую зависимость нашего слуха и в сумме станет линейной. При взгляде на рисунок это станет более понятно.

Зависимость сопротивления переменного резистора от угла поворота движка (А-линейная, Б-логарифмическая, В-показательная)
Здесь показаны графики зависимости сопротивления переменных резисторов разных типов: А – линейная, Б – логарифмическая, В – показательная. Как правило, на переменных резисторах отечественного производства указывается, какой зависимостью обладает переменный резистор. На тех же принципах основаны цифровые и электронные регуляторы громкости.
Также стоит отметить, что человеческое ухо воспринимает звуки, мощность которых различается на колоссальную величину в 10 000 000 000 000 раз! Таким образом, самый громкий звук отличается от самого тихого, который может уловить наш слух, на 130 дБ (10 000 000 000 000 раз).

Согласитесь, что куда проще при вычислениях использовать небольшие числа вроде 10, 20, 60,80,100,130 (наиболее часто используемые числа при расчёте в децибелах) по сравнению с числами 100 (20 дБ), 1000 (30 дБ), 1000 000 (60 дБ),100 000 000 (80 дБ),10 000 000 000 (100 дБ), 10 000 000 000 000 (130 дБ). Ещё одним достоинством децибел является то, что их просто суммируют. Если проводить вычисления в разах, то числа необходимо умножать.
Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.
Также децибелы очень удобны при графическом построении различных зависимостей. Все графики вроде диаграмм направленности антенн, амплитудно-частотных характеристик усилителей выполняют с применением децибел.
Децибел является безразмерной единицей измерения. Мы уже выяснили, что децибел на самом деле показывает, во сколько раз возросла, либо уменьшилась какая-либо величина (ток, напряжение, мощность). Отличие децибел от разов заключается лишь в том, что происходит измерение по логарифмическому масштабу. Чтобы это как-то обозначить и приписывают обозначение дБ. Так или иначе, при оценке приходится переходить от децибел к разам. Сравнивать с помощью децибел можно любые единицы измерения (не только ток, напряжение и проч.), так как децибел является относительной, безразмерной величиной.
Если указывается знак “-”, например, –1 дБ, то значение измеряемой величины, например, мощности, уменьшилось в 1,26 раз. Если перед децибелами не ставят никакого знака, то речь идёт об увеличении, росте величины. Это стоит учитывать. Иногда вместо знака “-” говорят о затуханиях, снижении коэффициента усиления.
Переход от децибел к разам.
На практике чаще всего приходится переходить от децибел к разам. Для этого есть простая формула:
Внимание! Данные формулы применяются для так называемых “энергетических” величин. Таких как энергия и мощность.
Например, 1дБ равен 10 (1дБ / 10) = 1,258925…= 1,26 раза.
при 20 дБ: 10 (20дБ / 10) = 100 (увеличение величины в 100 раз)
при 10 дБ: 10 (10дБ / 10) = 10 (увеличение в 10 раз)
Переход от разов к децибелам можно осуществить по следующей формуле:
Например, рост мощности в 4 раза будет соответствовать значению в 6,021 дБ.
10 * log10(4) = 6,021 дБ.
Внимание! Для пересчёта отношений таких величин как напряжение и сила тока существуют немного иные формулы:
(Сила тока и напряжение, это так называемые “силовые” величины. Поэтому и формулы отличаются.)
Для перехода к децибелам: n = 20 * log10(m)
Для перехода от децибел к разам: m = 10 (n / 20)
n – значение в децибелах, m – отношение в разах.
Если Вы успешно дошли до этих строк, то считайте, что сделали ещё один весомый шаг в освоении электроники!