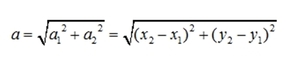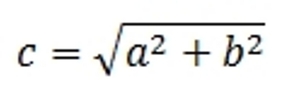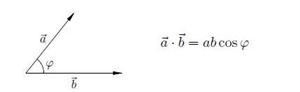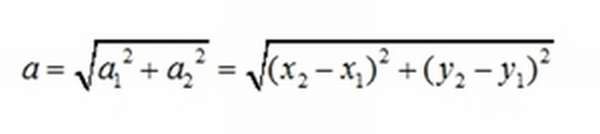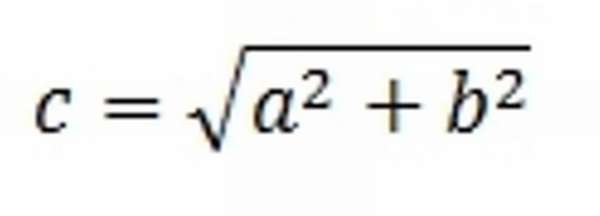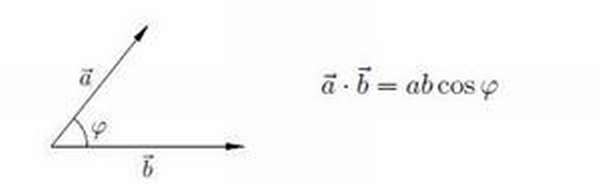Объясните какой вектор называется суммой двух векторов в чем
Какой вектор называется суммой двух векторов
Для правильного отображения законов природы в физике требуется соответствующий математический инструментарий.
В геометрии и физике есть величины, характеризующиеся и числовым значением, и направлением.
Их целесообразно изображать направленными отрезками или векторами.
У таких величин есть начало (отображается точкой) и конец, обозначаемый стрелкой. Длина отрезка называется модулем (длиной).
Координаты на плоскости
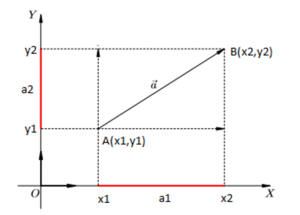
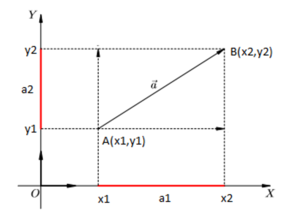
Зададим на плоскости отрезок, направленный из точки, А (x1,y1) в точку В (x2,y2). Его координатами a (a1, a2) являются числа а1=x2-x1, а2=y2-y1.
Модуль рассчитывается по теореме Пифагора: 
У нулевого вектора начало совпадает с концом. Координаты и длина равны 0.
Сумма векторов
Существуют несколько правил для расчета суммы
Правило сложения векторов можно объяснить на задачах из динамики и механики. Рассмотрим сложение векторов по правилу треугольника на примере сил, воздействующих на точечное тело и последовательных перемещений тела в пространстве.
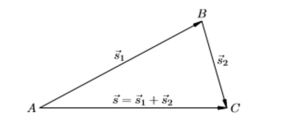
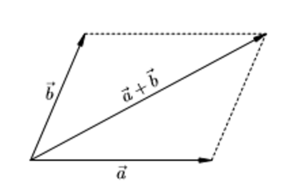
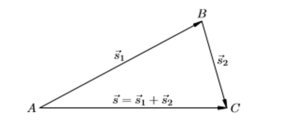
Допустим, тело переместилось сначала из точки A в точку B, а затем из точки B в точку C. Итоговое перемещение есть отрезок, направленный от начальной точки A к конечной точке C.
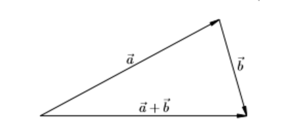
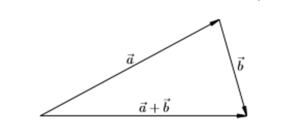
Результат двух перемещений или их сумма s = s1+ s2. Такой способ называется правилом треугольника.
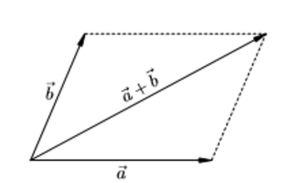
Стрелки выстраивают в цепочку одну за другой, при необходимости осуществляя параллельный перенос. Суммарный отрезок замыкает последовательность. Его начало совпадает с началом первого, конец — с концом последнего. В иностранных учебниках данный метод называется «хвост к голове».
Координаты результата c = a + b равны сумме соответствующих координат слагаемых c (a1+ b1, a2+ b2).
Сумма параллельных (коллинеарных) векторов также определяется по правилу треугольника.
Если два исходных отрезка перпендикулярны друг другу, то результат их сложения представляет собой гипотенузу построенного на них прямоугольного треугольника. Длина суммы вычисляется по теореме Пифагора.
Примеры:
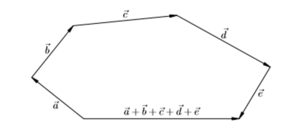
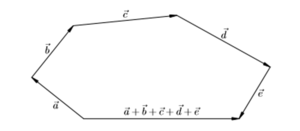
Сложение трех и более векторов производят по правилу многоугольника, «хвост к голове»
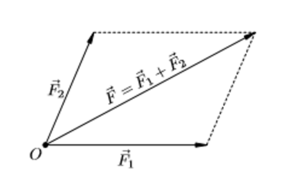
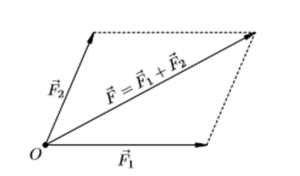
Предположим, что к точечному телу приложены силы F1 и F2.
Опыт доказывает, что совокупное воздействие этих сил равнозначно действию одной силы, направленной по диагонали построенного на них параллелограмма. Эта равнодействующая сила равна их сумме F = F1 + F 2. Приведенный способ сложения называется правилом параллелограмма.
Длина в этом случае вычисляется по формуле
, где θ — угол между сторонами.
Правила треугольника и параллелограмма взаимозаменяемы. В физике чаще применяют правило параллелограмма, так как направленные величины сил, скоростей, ускорений обычно приложены к одному точечному телу. В трехмерной системе координат применяется правило параллелепипеда.
Обратите внимание: что такое луч в геометрии.
Элементы алгебры
Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
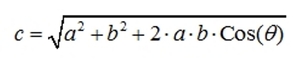
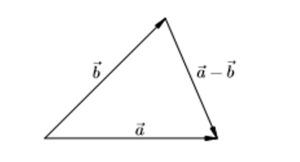
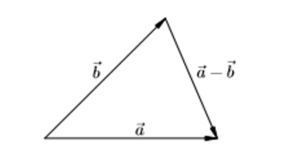
Для вычитания можно использовать видоизмененное правило треугольника.
Умножение на скаляр
Результатом умножения на скаляр будет вектор.
Координаты произведения получаются перемножением на скаляр соответствующих координат исходного.
Скаляр — числовая величина со знаком плюс или минус, больше или меньше единицы.
Примеры скалярных величин в физике:
Примеры:
Скалярное произведение направленных отрезков a и b равно произведению модулей на косинус угла между ними. Скалярное произведение взаимно перпендикулярных отрезков равно нулю.
Пример:
Какой вектор называется суммой двух векторов
Для правильного отображения законов природы в физике требуется соответствующий математический инструментарий.
В геометрии и физике есть величины, характеризующиеся и числовым значением, и направлением.
Их целесообразно изображать направленными отрезками или векторами.
У таких величин есть начало (отображается точкой) и конец, обозначаемый стрелкой. Длина отрезка называется модулем (длиной).
Это интересно: как переводить градусы в радианы?
Координаты на плоскости
Зададим на плоскости отрезок, направленный из точки, А (x1,y1) в точку В (x2,y2). Его координатами a (a1, a2) являются числа а1=x2-x1, а2=y2-y1.
Модуль рассчитывается по теореме Пифагора: 
У нулевого вектора начало совпадает с концом. Координаты и длина равны 0.
Сумма векторов
Существуют несколько правил для расчета суммы
Правило сложения векторов можно объяснить на задачах из динамики и механики. Рассмотрим сложение векторов по правилу треугольника на примере сил, воздействующих на точечное тело и последовательных перемещений тела в пространстве.
Допустим, тело переместилось сначала из точки A в точку B, а затем из точки B в точку C. Итоговое перемещение есть отрезок, направленный от начальной точки A к конечной точке C.
Результат двух перемещений или их сумма s = s1+ s2. Такой способ называется правилом треугольника.
Стрелки выстраивают в цепочку одну за другой, при необходимости осуществляя параллельный перенос. Суммарный отрезок замыкает последовательность. Его начало совпадает с началом первого, конец — с концом последнего. В иностранных учебниках данный метод называется «хвост к голове».
Координаты результата c = a + b равны сумме соответствующих координат слагаемых c (a1+ b1, a2+ b2).
Сумма параллельных (коллинеарных) векторов также определяется по правилу треугольника.
Если два исходных отрезка перпендикулярны друг другу, то результат их сложения представляет собой гипотенузу построенного на них прямоугольного треугольника. Длина суммы вычисляется по теореме Пифагора.
Примеры:
Сложение трех и более векторов производят по правилу многоугольника, «хвост к голове»
Предположим, что к точечному телу приложены силы F1 и F2.
Опыт доказывает, что совокупное воздействие этих сил равнозначно действию одной силы, направленной по диагонали построенного на них параллелограмма. Эта равнодействующая сила равна их сумме F = F1 + F 2. Приведенный способ сложения называется правилом параллелограмма.
Длина в этом случае вычисляется по формуле
, где θ угол между сторонами.
Правила треугольника и параллелограмма взаимозаменяемы. В физике чаще применяют правило параллелограмма, так как направленные величины сил, скоростей, ускорений обычно приложены к одному точечному телу. В трехмерной системе координат применяется правило параллелепипеда.
Обратите внимание: что такое луч в геометрии.
Элементы алгебры
Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
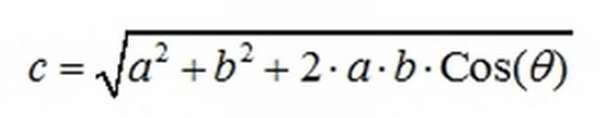
Для вычитания можно использовать видоизмененное правило треугольника.
Умножение на скаляр
Результатом умножения на скаляр будет вектор.
Координаты произведения получаются перемножением на скаляр соответствующих координат исходного.
Скаляр — числовая величина со знаком плюс или минус, больше или меньше единицы.
Примеры скалярных величин в физике:
Примеры:
Скалярное произведение направленных отрезков a и b равно произведению модулей на косинус угла между ними. Скалярное произведение взаимно перпендикулярных отрезков равно нулю.
Пример: