Объясните что такое отрезок кратко
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
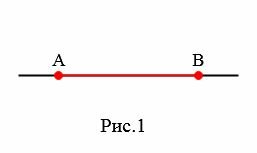 |
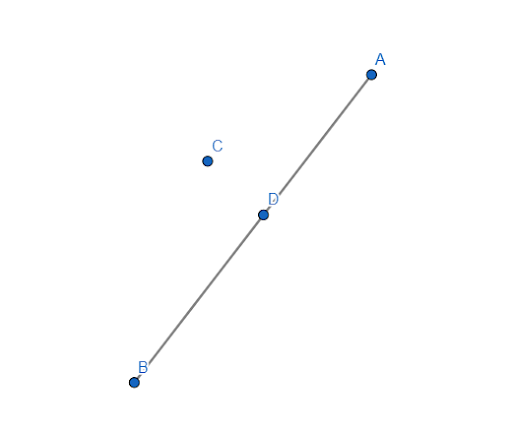
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
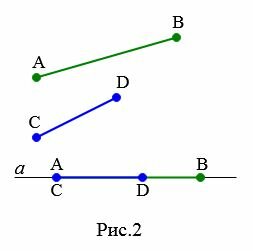 |
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
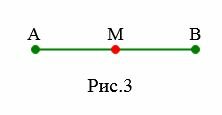 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
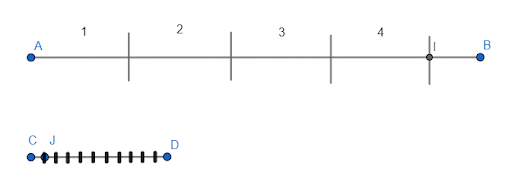
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
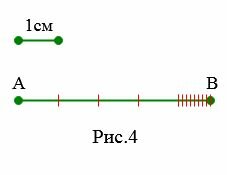 |
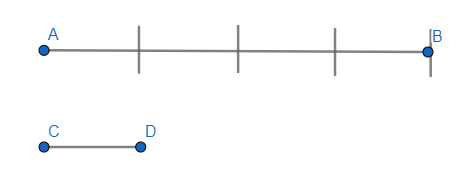
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
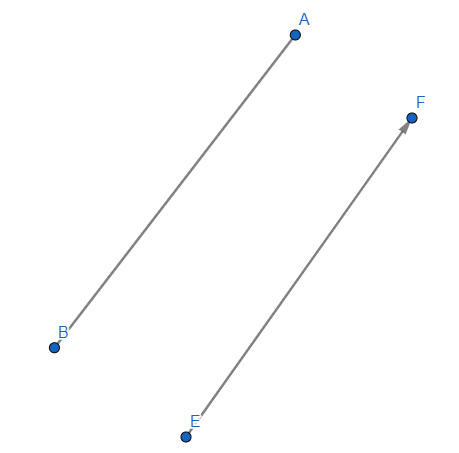
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
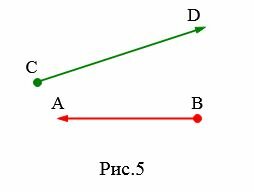 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Объясните,что такое отрезок?
Ответ или решение 2
Длиной отрезка является расстояние между его концами.
Примеры отрезков в геометрических фигурах
Во многих фигурах отрезок является их составной частью. Перечислить все фигуры, которые включают в себя отрезки, невозможно, но назовем некоторые из них. Рассмотрим следующие:
Примеры задач об отрезках
1. На отрезке АВ длиной 9 см лежит точки С и К, причем они делят отрезок на 3 равные части. Определить величину СК.
Точки С и К делят отрезок на 3 равные части, значит АС = СК = КВ = АВ / 3 = 9 / 3 =
2. Отрезки АВ = 1 см, ВС = 2 см, СК = 3 см и КО = 4 см составляют ломанную линию. Найти длину АВСКО.
Длина АВСКО равна сумме длин всех входящих в нее отрезков АВСКО = АВ + ВС + СК + КО = 1 + 2 + 3 + 4 = 10 см.
Отрезок — это множество, которое состоит из двух точек, расположенных на прямой (концы отрезка), и точек, которые лежат между ними. Концы отрезка обычно обозначают латинскими буквами: A и B, C и D, M и K и т. д. Сам же отрезок обозначают по названию его концов, то есть: отрезок с концами A и B будет обозначаться как AB. Расстояние между точками, являющимися концами отрезка, называется длиной отрезка и обозначается |AB| (так как длина отрезка не может быть отрицательной). Длину отрезка можно вычислить, зная координаты конца и начала отрезка.
Пусть концы отрезка AB имеют координаты A (x₁; y₁) и B (x₂; y₂). Тогда длина AB вычисляется по формуле:
Как определяется понятие «отрезок» в геометрии
Содержание:
Для изображения прямых, лучей и отрезков применяют линейку. Отрезок на листике бумаги можно изобразить полностью, для луча и прямой – их фрагменты, ведь первый не имеет конца, только начало, вторая – бесконечна. Объясним, что такое отрезок в геометрии, чем отличается от иных фигур в евклидовом пространстве. Разберёмся с его свойствами.
Как выглядит отрезок
Обозначается двумя буквами – это название точек, лежащих в начале и конце. AB – концы геометрической фигуры, а расстояние между ними – длина фигуры, обозначается |AB|, измеряется преимущественно в сантиметрах.
Количество первых и вторых может быть любым.
Различают следующие отрезки:
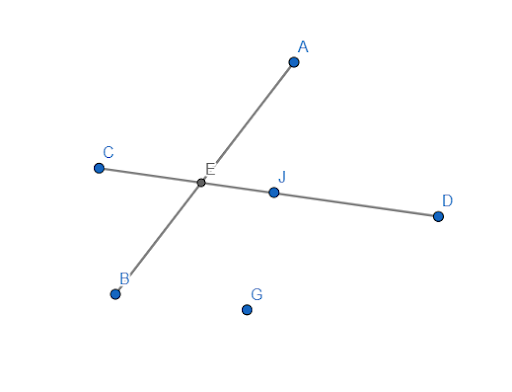
Выше показаны расположенные в одной точке пересекающиеся отрезки, имеющие общую точку – E. Два обрезка не могут иметь больше одной общей точки.
Разнообразие и измерение отрезков
Геометрическая фигура AB тождественна или равная BA. Началом и концом может быть любая буква A или B, разницы нет. В случае с вектором фигура EF не равная FE.
Измерение геометрических фигур основано на аксиоме Архимеда: дана пара отрезков разной длины, причём AB > CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.
CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.» src=»https://455811.selcdn.ru/BINGOCDN/default/moddocument/3023/e374aa7c42abc85c5922eca722ecfd2f1c4ee8aa.png» />
На практике их длина измеряется линейкой. Начальная точка совмещается с обозначением ноля на именительном приборе, точность которого равна одному миллиметру. Если конечная точка лежит между рисками на линейке, разницу в доли миллиметра не учитывают – значение округляют.
При измерении бывают следующие случаи (при условии, что AB > CD):
В подобных случаях обходятся избыточным и недостаточным измерениями. В первом – дробь округляют в меньшую сторону: если получается более 5,6, записывают 5,6; во втором – 5,7 см.
Значение слова «отрезок»
1. Небольшой отрезанный кусок чего-л. Отрезки ткани.□ Агафья Матвеевна сидела на полу и перебирала рухлядь в старом сундуке; около нее лежали груды тряпок, ваты, старых платьев, пуговиц и отрезков мехов. И. Гончаров, Обломов.
2. Часть чего-л., ограниченная часть какого-л. целого. Отрезок линии. Отрезок времени. □ Последний отрезок пути пришлось ехать в теплушке. А. Н. Толстой, Хмурое утро. Надо, чтобы каждая строка заключала в себе вполне законченный отрезок фразы, если не всю фразу. Исаковский, О поэтическом мастерстве.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ОТРЕ’ЗОК, зка, м. 1. Небольшой отрезанный кусок. Отрезки ткани. 2. чаще мн. Земельные участки, захваченные помещиками у крестьян после отмены крепостного права в 1861 г. (истор.). Существование отрезков являлось одним из источников отработочной системы. 3. Ограниченная часть чего-н. (книжн. и мат.). О. пути. О. линии. О. времени (нов.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
отре́зок
1. кусок чего-либо, отделённый от более крупного куска
2. перен. часть объекта, имеющего пространственное или временное измерение
3. геометр. часть линии между двумя точками ◆ Каждый отрезок имеет определённую длину, большую нуля. А. В. Погорелов, «Геометрия, учебник для 7-11 классов», 1999 г.
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова фильдеперсовый (прилагательное):
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.