Объясните что такое отрезок 7 класс
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
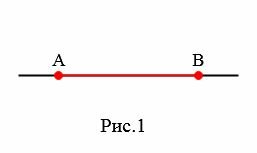 |
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
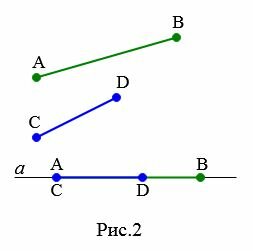 |
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
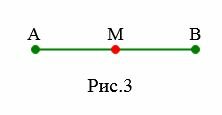 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
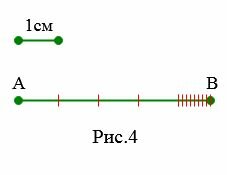 |
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
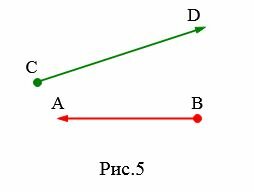
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Объясните,что такое отрезок?
Ответ или решение 2
Длиной отрезка является расстояние между его концами.
Примеры отрезков в геометрических фигурах
Во многих фигурах отрезок является их составной частью. Перечислить все фигуры, которые включают в себя отрезки, невозможно, но назовем некоторые из них. Рассмотрим следующие:
Примеры задач об отрезках
1. На отрезке АВ длиной 9 см лежит точки С и К, причем они делят отрезок на 3 равные части. Определить величину СК.
Точки С и К делят отрезок на 3 равные части, значит АС = СК = КВ = АВ / 3 = 9 / 3 =
2. Отрезки АВ = 1 см, ВС = 2 см, СК = 3 см и КО = 4 см составляют ломанную линию. Найти длину АВСКО.
Длина АВСКО равна сумме длин всех входящих в нее отрезков АВСКО = АВ + ВС + СК + КО = 1 + 2 + 3 + 4 = 10 см.
Отрезок — это множество, которое состоит из двух точек, расположенных на прямой (концы отрезка), и точек, которые лежат между ними. Концы отрезка обычно обозначают латинскими буквами: A и B, C и D, M и K и т. д. Сам же отрезок обозначают по названию его концов, то есть: отрезок с концами A и B будет обозначаться как AB. Расстояние между точками, являющимися концами отрезка, называется длиной отрезка и обозначается |AB| (так как длина отрезка не может быть отрицательной). Длину отрезка можно вычислить, зная координаты конца и начала отрезка.
Пусть концы отрезка AB имеют координаты A (x₁; y₁) и B (x₂; y₂). Тогда длина AB вычисляется по формуле:
Зачёт по геометрии за 7 класс
Вопросы по геометрии. 7 класс
1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Что такое отрезок? Начертить, обозначить и объяснить? Какая точка называется серединой отрезка?
4. Что такое луч? Как обозначаются лучи?
5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
6. Какие фигуры называются равными?
7. Как сравнить два угла? Какой луч называется биссектрисой угла?
8. Какой угол называется острым? прямым? тупым?
9. Какие углы называются смежными? Чему равна сумма смежных углов? Уметь их строить.
10. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Уметь их строить.
11. Какие прямые называются перпендикулярными? Уметь их строить Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются?
12. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?
13. Какие треугольники называются равными?
14. Что такое теорема и доказательство теоремы?
15. Сформулируйте первый признак равенства треугольников.
16. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Уметь их строить.
17. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Уметь их строить.
18. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Уметь их строить.
19. Какой треугольник называется равнобедренным? Уметь его строить. Как называются его стороны?
20. Какой треугольник называется равносторонним? Уметь его строить. Сформулировать основные свойства равнобедренного треугольника.
21. Сформулируйте второй признак равенства треугольников.
22. Сформулируйте третий признак равенства треугольников.
23. Что такое определение? Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?
24. Объясните, как отложить от данного луча в данную плоскость угол, равный данному.(с помощью циркуля и линейки)
25. Объясните как построить биссектрису данного угла.( с помощью циркуля и линейки)
28. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
31. Что такое аксиома? Приведите примеры. Сформулируйте аксиому параллельных прямых.
32. Какая теорема называется обратная данной теореме? Приведите примеры теорем, обратных данным.
33. Сформулируйте теоремы об углах, образованных двумя параллельными прямыми и секущей.
34. Сформулируйте теорему о сумме углов треугольника.
35. Какой угол называется внешним углом треугольника? Уметь его строить. Сформулируйте, чему равен внешний угол в треугольнике.
36. Какой треугольник называют остроугольным? Какой треугольник называется тупоугольным? Уметь их строить.
37. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
38. Сформулируйте соотношения между сторонами и углами. Почему в прямоугольном треугольнике гипотенуза больше катета?
39. Сформулируйте теорему о неравенстве треугольника.
40. Сформулируйте некоторые свойства прямоугольных треугольников.
41. Сформулируйте признаки равенства прямоугольных треугольников.
42. Что называется расстоянием от точки до прямой?
43. Что называется расстоянием между двумя параллельными прямыми?
44. Объясните, как построить треугольник по двум сторонам и углу между ними.
45. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.
46. Объясните, как построить треугольник по трём сторонам. Всегда ли эта задача имеет решение?
Задачи к зачету по геометрии. 7 класс
Задача №1. В равнобедренном треугольнике угол при основании в 2 раза меньше, чем угол при вершине. Найдите все углы треугольника.
Задача №2. Высота АD равностороннего треугольника ВАС с основанием ВС равна 10 см, периметр треугольника АDС равен 70 см. Найдите периметр треугольника АВС.
Задача №3. Первый угол треугольника равен 40градусов, а второй больше третьего на 16 градусов. Найдите эти углы треугольника.
Задача №4. В равнобедренном треугольнике периметр равен 150 см, боковая сторона больше основания на 15 см. Найдите все стороны треугольника.
Задача №5. В равнобедренном прямоугольном треугольнике гипотенуза равна 42 см. Найдите высоту проведённую из вершины прямого угла.
Задача №6. В равнобедренном треугольнике внешний угол при вершине равен 40 градусов. Найдите углы этого треугольника.
Задача №7. В равнобедренном треугольнике СDЕ с основанием СЕ проведена биссектриса СF. Найдите угол ЕСF, если угол D равен 54 градуса.
Задача №8. Один из углов прямоугольного треугольника равен 60 градусов, а сумма гипотенузы и меньшего катета равна 30 см. Найдите гипотенузу треугольника.
Задача №9. Один из внешних углов равнобедренного треугольника равен 110 градусов. Найдите все углы данного треугольника.
Задача №10. Периметр равнобедренного треугольника равен 65 см, его боковая сторона на 5 см меньше основания. Найдите стороны треугольника.
Задача №11. Периметр равнобедренного тупоугольного треугольника равен 77 см, а одна из его сторон больше другой на 17см. Найдите стороны этого треугольника.
Задача №12. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 градусов. Найдите угол ВОD.
Задача №13. В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NК в точке О. причём ОК равно 9 см.
Найдите расстояние от точки О до прямой МN.
Задача №14. Отрезки АВ и СD- диаметры окружности с центром О. Найдите периметр треугольника АОD, если хорда СВ равна 10 см, диаметр АВ равен 12 см.
Задача №15. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 296 градусов.
Задача №16. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если угол АОВ равен 110 градусов, а угол АОС на 18 градусов меньше угла ВОС.
Задача №17. Углы треугольника относятся как 2: 3: 4. Найдите их градусные меры.
Задача №18. В равнобедренном треугольнике АВС с основанием АС равно 38 см внешний угол при вершине В равен 60 градусов. Найдите расстояние от вершины С до прямой АВ.
Задача №19. Один из углов при пересечении двух параллельных прямых третьей прямой в 2 раза больше другого. Найдите остальные углы.
Задача №20. Один из углов при пересечении двух параллельных прямых третьей прямой на 20 градусов меньше другого. Найдите остальные углы.
Задача №21. В равнобедренном треугольнике АВС с основанием АС равно 42см, внешний угол при вершине С равен 120 градусов. Найдите боковые стороны треугольника АВС.
Конспект урока геометрии в 7 классе «Сравнение отрезков и углов»
Данный конспект позволяет ввести одно из важнейших геометрических понятий — понятие равенства фигур, в частности равенства отрезков и углов, научить учащихся сравнивать отрезки и углы, ввести понятия середины отрезка и биссектрисы угла.
Просмотр содержимого документа
«Конспект урока геометрии в 7 классе «Сравнение отрезков и углов»»
Сравнение отрезков и углов
Образовательная: ввести одно из важнейших геометрических понятий — понятие равенства фигур, в частности равенства отрезков и углов, научить учащихся сравнивать отрезки и углы, ввести понятия середины отрезка и биссектрисы угла.
Развивающая: развивать память, мышление, внимание, восприятие;
Воспитательная: воспитывать устойчивый интерес к изучению геометрии, трудолюбие, аккуратность, терпение.
1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Объясните, что такое отрезок.
4. Объясните, что такое луч. Как обозначаются лучи?
5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
6. Какой угол называется развернутым?
1. Начертите неразвернутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
2. Начертите неразвернутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
3. Начертите неразвернутый угол АОВ и проведите:
а) луч ОС, который делит угол АОВ на два угла;
б) луч OD, который не делит угол АОС на два угла.
Объяснение нового материала.
Понятие равенства геометрических фигур вводится на основе понятия наложения. Разумеется, учащиеся VII класса должны воспринимать это понятие так, как мы его наглядно представляем, а не как отображение плоскости на себя, свойства которого выражены в аксиомах. Поэтому при введении понятия равенства фигур желательно использовать модели различных плоских фигур (знакомых учащимся из курса математики I—VI классов), для которых можно установить равенство непосредственным наложением одной фигуры на другую, а также плакат с фигурами Ф1 и Ф2, аналогичный рисунку 19 учебника, и кальку, с помощью которой можно показать процесс наложения одной фигуры на другую, описанный в учебнике.
При изучении п. 5 следует обратить внимание учащихся на то, что задача сравнения фигур (их форм и размеров) является одной из основных задач в геометрии. На практике сравнить наложением две небольшие плоские фигуры вполне возможно, а вот два очень больших стекла, а тем более два земельных участка практически невозможно. Это приводит к необходимости иметь какие-то правила сравнения двух фигур, позволяющие сравнить некоторые их размеры и по результатам этого сравнения сделать вывод о равенстве или неравенстве фигур.
Задание 1: Сравнить несколько отрезков, изображенных на доске, среди которых есть равные (с помощью кальки, бечевки или циркуля).
Самостоятельная работа (в форме диктанта).
1. На луче ОК отложите отрезки О А и О В так, чтобы точка А лежала между точками О и В. Сравните отрезки ОА и ОВ и запишите результат сравнения.
Начертите неразвернутый угол ABC и проведите какой-нибудь луч BD, делящий этот угол на два угла. Сравните углы ABC и ABD, ABC и DBC и запишите эти результаты сравнения.
5. Домашнее задание: п.п. 5, 6; вопросы 7—11 (с. 25); задачи 18, 23.














