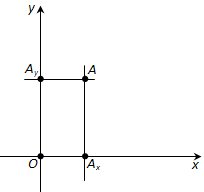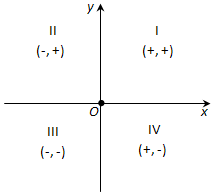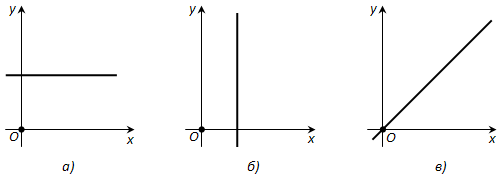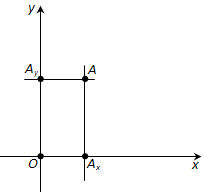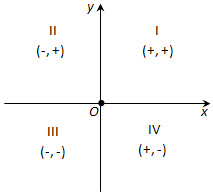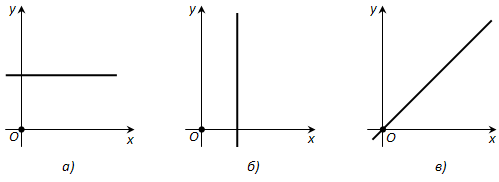Объясните что такое ось координат начало координат положительная полуось отрицательная

14.10.202323.08.2023 admin 0 Comments

Объясните что такое ось координат начало координат положительная полуось отрицательная

Вопрос 1. Объясните, как определяются координаты точки.
Ответ. Проведём на плоскости через точку O две взаимно перпендикулярные прямые x и y – оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось y – осью ординат. Точкой пересечения O – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая её стрелкой, а другую – отрицательной.

Каждой точке A плоскости мы сопоставим пару чисел – координаты точки – абсциссу (x) и ординату (y) по такому правилу.
Через точку A проведём прямую, параллельную оси ординат (рис. 171). Она пересечёт ось абсцисс x в некоторой точке A_x. Абсциссой точки A мы будем называть число x, абсолютная величина которого равна расстоянию от точки O до точки A_x. Это число будет положительным, если Ax принадлежит положительной полуоси и отрицательным, если A_xпринадлежит отрицательной полуоси. Если точка A лежит на оси ординат y, то полагаем x равным нулю.

Ордината (y) точки A определяется аналогично. Через точку A проведём прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечёт ось ординат y в некоторой точке A_y. Ординатой точки A мы будем называть число y, абсолютная величина которого равна расстоянию от точки O до точки A_y. Это число будет положительным, если A_y принадлежит положительной полуоси и отрицательным, если A_y принадлежит отрицательной полуоси. Если точка A лежит на оси абсцисс x, то полагаем y равным нулю.
Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: A (x; y) (на первом месте абсцисса, на втором – ордината).

Вопрос 2. Какие знаки у координат точки, если она принадлежит первой (второй, третьей, четвёртой) четверти?
Ответ. Оси координат разбивают плоскость на четыре части – четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения.

Если точка принадлежит первой четверти, то её абсцисса и ордината будут положительными.
Если точка принадлежит второй четверти, то её абсцисса будет отрицательной, а ордината будет положительной.
Если точка принадлежит третьей четверти, то её абсцисса и ордината будут отрицательными.
Если точка принадлежит четвёртой четверти, то её абсцисса будет положительной, а ордината будет отрицательной.

Вопрос 3. Чему равны абсциссы точек, лежащих на оси ординат?
Чему равны ординаты точек, лежащих на оси абсцисс?
Чему равны координаты начала координат?
Ответ. Точки оси x (оси абсцисс) имеют равные нулю ординаты (y = 0), а точки оси y (оси ординат) имеют равные нулю абсциссы (x = 0).
Если какая-либо точка лежит на оси ординат y, то абсцисса данной точки равна нулю.
Если какая-либо точка лежит на оси абсцисс x, то ордината данной точки равна нулю.
У начала координат абсцисса и ордината равны нулю.

Вопрос 4. Выведите формулы для координат середины отрезка.
Ответ. Пусть A (x₁; y₁) и B (x₂;y₂) – две произвольные точки и C (x; y) – середина отрезка AB. Найдём координаты x, y точки C.
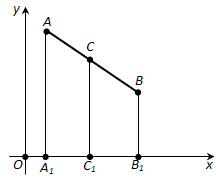
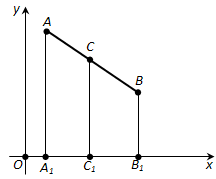
Рассмотрим сначала случай, когда отрезок AB не параллелен оси y, т.е. \(x_1 \neq x_2\). Проведём через точки A, B, C прямые, параллельные оси y (рис. 173). Они пересекут ось x в точках A1 (\(x_1\); 0), B1 (\(x_2\); 0), C (\(x\); 0). По теореме Фалеса точка \(C_1\) будет серединой отрезка \(A_1B_1\).

Если \(x_1 = x_2\), т.е. отрезок AB параллелен оси y, то все три точки \(A_1, B_1, C_1\) имеют одну и ту же абсциссу. Значит, формула остаётся верной и в этом случае.
Ордината точки C находится аналогично. Через точки A, B, C проводятся прямые, параллельные оси x. Получается формула

Вопрос 5. Выведите формулу для расстояния между точками.
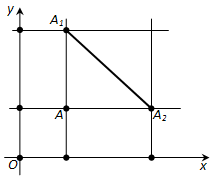
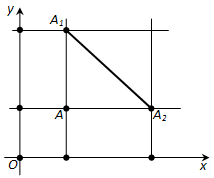
Ответ. Пусть на плоскости xy даны две точки: \(A_1\) с координатами \(x_1, y_1\) и \(A_2\) с координатами \(x_2, y_2\). Выразим расстояние между точками \(A_2\) и \(A_2\) через координаты этих точек.
Рассмотрим сначала случай, когда \(x_1 \neq x_2\) и \(y_1 \neq y_2\). Проведём через точки \(A_1\) и \(A_2\) прямые, параллельные осям координат, и обозначим через A точку их пересечения (рис. 174). Расстояние между точками \(A\) и \(A_1\) равно \(|y_1 – y_2|\), а расстояние между точками \(A\) и \(A_2\) равно \(|x_1 – x_2|\). Применяя к прямоугольному треугольнику \(AA_1A_2\) теорему Пифагора, получим:

где d –расстояние между точками \(A_1\) и \(A\).

Вопрос 6. Что такое уравнение фигуры в декартовых координатах?
Ответ. Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными x и y, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры.

Вопрос 7. Выведите уравнение окружности.
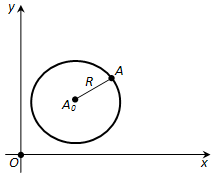
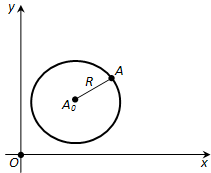
Ответ. Составим уравнение окружности с центром в точке A_O (a; b) и радиусом R (рис. 175). Возьмём произвольную точку A (x; y) на окружности. Расстояние от неё до центра A_O равен \((x – a)^2 + (y – b)^2\). Таким образом, координаты x, y каждой точки A окружности удовлетворяют уравнению

Обратно: любая точка A, координаты которой удовлетворяют уравнению (*), принадлежит окружности, так как расстояние от неё до точки A_O равно R. Отсюда следует, что уравнение (*) действительно является уравнением окружности с центром A_Oи радиусом R. Заметим, что если центром окружности является начало координат, то уравнение окружности имеет вид:

Вопрос 8. Докажите, что прямая в декартовых координатах имеет уравнение вида ax + by + c = 0.
Ответ. Докажем, что любая прямая в декартовых координатах x, y имеет уравнение вида

где a, b, c – некоторые числа.
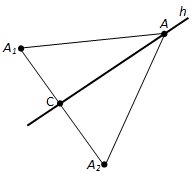
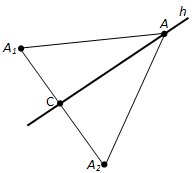
Пусть h – произвольная прямая на плоскости xy. Проведём какую-нибудь прямую, перпендикулярную прямой h, и отложим на ней от точки пересечения C с прямой h равные отрезки CA₁ и CA₂(рис. 176).

Пусть a₁, b₁ – координаты точки A₁ и a₂, b₂ – координаты точки A₂. Как мы знаем, любая точка A (x; y) прямой h равноудалена от точек A₁ и A₂. Поэтому координаты её удовлетворяют уравнению

Обратно: если координаты x и y какой-нибудь точки удовлетворяют уравнению (**), то эта точка равноудалена от точек A₁ и A₂, а значит, принадлежит прямой h. Таким образом, уравнение (**) является уравнением прямой h. Если в этом уравнении раскрыть скобки и перенести все члены уравнения в левую его часть, то оно примет вид:

Вопрос 9. Как найти координаты точки пересечения двух прямых, если заданы уравнения этих прямых?
Ответ. Пусть заданы уравнения двух прямых:

Найдём координаты их точки пересечения.
Так как точка пересечения (x; y) принадлежит каждой из прямых, то её координаты удовлетворяют и первому и второму уравнению. Поэтому координаты точки пересечения являются решением системы уравнений, задающих прямые. Рассмотрим пример.
Пусть уравнениями данных прямых будут:

Вопрос 10. Как расположена прямая, если в её уравнении коэффициент a = 0 (b = 0; c = 0)?
Ответ. Выясним, как расположена прямая относительно осей координат, если её уравнение ax + by + c = 0 имеет тот или иной частный вид.
1. a = 0, b \(\neq\) 0. В этом случае уравнение прямой можно переписать так:

Таким образом, все точки прямой имеют одну и ту же ординату (\(-\frac\)); следовательно, прямая параллельна оси x (рис. 177, а). В частности, если c = 0, то прямая совпадает с осью x.
2. b = 0, a \(\neq\) 0. Этот случай рассматривается аналогично. Прямая параллельна оси y (рис. 177, б) и совпадает с ней, если c = 0.

3. c = 0. Прямая проходит через начало координат, так как его координаты (0; 0) удовлетворяют уравнению прямой (рис. 177, в).

Источник

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Источник

Прямоугольная система координат

В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.

Координаты могут обозначаться самыми разными наборами цифр или букв.

Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.

Координаты — это набор данных, по которому определяется положение того или иного объекта.

Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.

Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.

Декартова система координат

Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.

Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.

Оси взаимно перпендикулярны (т.е. угол между ними равен 90° ) и пересекаются в точке, которую обозначают « O ». Точка « O » является началом отсчёта для каждой из осей.

Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.

Координатные оси — это прямые, образующие систему координат.

Ось абсцисс « Ox » — горизонтальная ось.

Ось ординат « Oy » — вертикальная ось.

Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как « x0y ».

Обращаем ваше внимание на выбор длины единичных отрезков по осям.

Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси « Oy ». Цифры на оси « Ox », как правило, пишут внизу под осью.

Обычно единичный отрезок на оси « 0y » равен единичному отрезку на оси « 0x ». Но бывают случаи, когда они не равны друг другу.

Отсчитываем четверти (или координатные углы) против часовой стрелки.

Источник