Объясните что такое множество элемент множества

Множества

Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.

Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:

N — множество натуральных чисел,

Z — множество целых чисел.

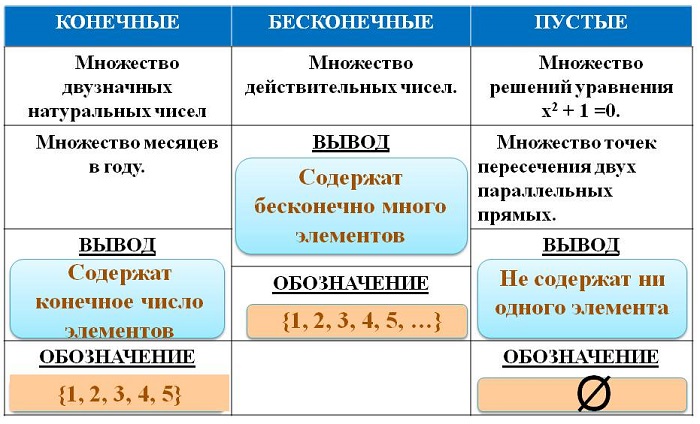
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.

Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись

означает, что множество L состоит из четырёх чётных чисел.

Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.

Подмножество

Подмножество — это множество, все элементы которого, являются частью другого множества.

Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.

Рассмотрим два множества:

Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :

Рассмотрим два множества:

Так как оба множества состоят из одних и тех же элементов, то L = M.

Пересечение и объединение множеств

Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.

При объединении равных множеств объединение будет равно любому из данных множеств:

Источник

Понятие множества и элемента множества

Множество – одно из основных понятий современной математики, используемое почти во всех ее разделах.

Во многих вопросах приходится рассматривать некоторую совокупность элементов как единое целое. Так, биолог, изучая животный мир и растительный мир данной области, классифицирует все особи по видам, виды по родам. Каждый вид является некоторой совокупность живых существ, рассматриваемой как единое целое.

Для математического описания таких совокупностей и было введено понятие множества. По словам одного из создателей теории множеств – немецкого математика Георга Кантора (1845–1918), «множество есть многое, мыслимое нами как целое». Разумеется, эти слова не могут рассматриваться как математически строгое определение множества, такового определения не существует, поскольку понятие множества является исходным, на основе которого строятся остальные понятия математики. Но из этих слов ясно, что можно говорить о множестве чисел от 1 до 10, натуральных числах, множестве треугольников и квадратов на плоскости.

Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве учащихся некоторого класса, о множестве гласных букв русского алфавита, о множестве натуральных чисел.

Математический смысл слова «множество» отличается от того, как оно используется в обычной речи, где его связывают с большим количеством предметов. В математике этого не требуется. Здесь рассматривают множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.

В основном множества обозначают буквами латинского алфавита: A, B, C, …, Z, L.

Определение. Множество, не содержащее ни одного объекта, называют пустым и обозначают знакомÆ.

Определение. Объекты, из которых образовано множество, называют его элементами.

Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c, …, z.

В математике и других науках нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Например, мы говорим, что число 5 натуральное. Другими словами, число 5 принадлежит множеству натуральных чисел. Или, например, число 0,45 не является натуральным числом. Это означает, что число 0,45 не принадлежит множеству натуральных чисел.

Предложение вида “ Объект а принадлежит множеству А” можно записать, используя символы: аÎА. Прочитать его можно по-разному:

Объект а принадлежит множеству А.

Объект а – элемент множества А.

Множество А содержит элемент а.

Предложение “ Объект а не принадлежит множеству А” можно записать так: а Ï А. Его читают:

Объект а не принадлежит множеству А.

Объект а не является элементом множества А.

Множество А не содержит элемента а.

Пусть А – множество однозначных чисел. Тогда предложение “7ÎА” можно прочитать: “Число 7 однозначное”, а запись “ 14Ï А” означает: “Число 14 не является однозначным”.

Множества бывают конечными и бесконечными. Так, множество дней недели конечно, а множество точек прямой бесконечно. Бесконечными множествами являются и такие множества, как множество натуральных чисел (N), множество целых чисел (Z), множество рациональных чисел (Q), множество действительных чисел (R).

Источник

Элемент множества

Мно́жество — один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).

Содержание

Теории

Существует два основных подхода к понятию множества — наивная и аксиоматическая теория множеств.

«Наивная теория множеств»

Дать определение какому-нибудь понятию — это значит описать это понятие через понятия, определённые ранее. Если число определений в теории конечно, то первое определение должно быть основано на понятиях, которые являются аксиоматическими, то есть изначально неопределёнными. Множество — как раз одно из таких аксиоматических понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам, возникающим из-за того, что интуитивное понятие «чётко определённый» на самом деле само не определено чётко. Так как теория множеств, фактически, используется как основание и язык всех современных математических теорий, становится очевидной необходимость её строгой аксиоматизации.

Наивная теория множеств была создана Кантором в конце XIX века.

История определения

До XIX века считалось, что точного определения множества нет. Множеством считалось любое скопление предметов.

Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.

Аксиоматическая теория множеств

На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).

Элемент множества

Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а∉А(а не принадлежит А).

Некоторые виды множеств

Множество множеств Подмножество Надмножество

Операции над множествами

Литература

См. также

Полезное

Смотреть что такое «Элемент множества» в других словарях:

элемент множества — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] элемент множества Объект любой природы, который в совокупности с другими аналогичными объектами составляет множество. Часто вместо термина элемент в… … Справочник технического переводчика

Элемент множества — [ele­ment of a set] объект любой природы, который в совокупности с другими аналогичными объектами составляет множество. Часто вместо термина элемент в этом смысле употребляют «точка множества», «член множества» и др.… … Экономико-математический словарь

МНОЖЕСТВА — МНОЖЕСТВА, в математике совокупность определенных объектов. Эти объекты называются элементами множества. Число элементов может быть бесконечным или конечным, или даже равняться нулю (число элементов в пустом множестве обозначается 0). Каждый… … Научно-технический энциклопедический словарь

элемент — Обобщенный термин, под которым в зависимости от соответствующих условий может пониматься поверхность, линия, точка. Примечания 1. Элемент может быть поверхностью (частью поверхности, плоскостью симметрии нескольких поверхностей), линией (профилем … Справочник технического переводчика

Элемент — часть чего нибудь. Одна из возможных этимологий этого слова по названию ряда согласных латинских букв L, M, N (el em en). Элемент (философия) Элемент обязательная принадлежность флага, знамени и штандарта. Элемент множества Элементарные… … Википедия

Элемент — [element] первичная (для данного исследования, модели) составная часть сложного целого. См. Элемент множества, Элемент системы … Экономико-математический словарь

Элемент (математика) — Множество один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном… … Википедия

элемент — 02.01.14 элемент (знак символа или символ) [element ]: Отдельный штрих или пробел в символе штрихового кода либо одиночная многоугольная или круглая ячейка в матричном символе, формирующие знак символа в… … Словарь-справочник терминов нормативно-технической документации

элемент — а; м. [от лат. elementum стихия, первоначальное вещество] 1. Составная часть чего л.; компонент. Разложить целое на элементы. Из каких элементов состоит культура? Природа э. производства. Составные элементы чего л. // Характерное движение, одна… … Энциклопедический словарь

Элемент (философия) — У этого термина существуют и другие значения, см. Элемент. Элемент (лат. elementum стихия) самостоятельная часть, являющаяся основой чего либо, например системы или множества. Этимология Латинское слово elementum использовали ещё … Википедия

Источник

Множества,их элементы,поджмножества

Вы будете перенаправлены на Автор24

В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.

Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.

Виды множеств

Множества могут быть конечными и бесконечными, пустыми.

Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.

Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.

Множество, не являющееся конечным, называют бесконечным множеством.

Подмножества

Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.

Например, из множества натуральных чисел можно выделить множество четных.

Обозначение множеств, подмножеств и их элементов

Готовые работы на аналогичную тему

\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ <\rm :\ >54\in A.\]

Способы задания множеств

Существует два глобально различных способа задания множеств.

Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него

При таком способе задания множеств говорят, что множество задано перечислением его элементов.

Равенство множеств

Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.

Например, рассмотрим множества

Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны

Пересечение множеств

Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.

Например, рассмотрим два множества:

Объединение множеств

Математически это можно обозначить так:$\ А\ \cup B$

Разность множеств

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 05 2021

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

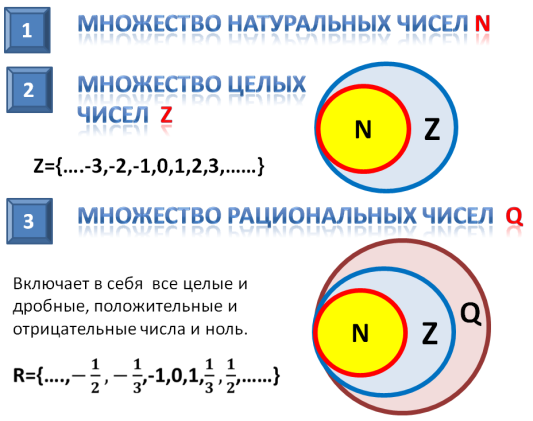
Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

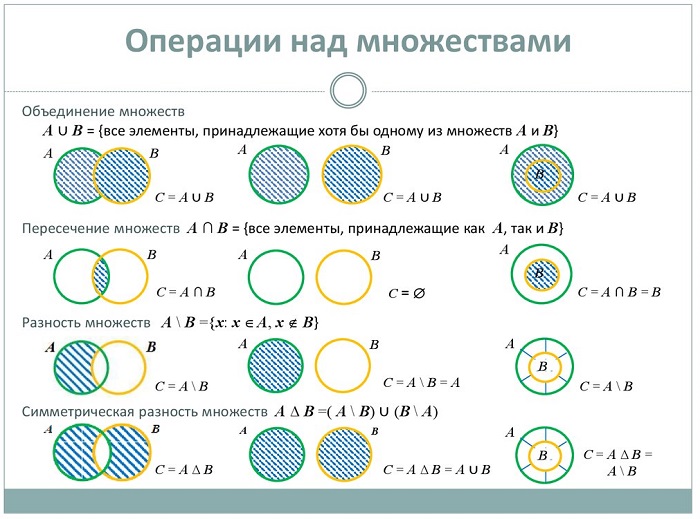
Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

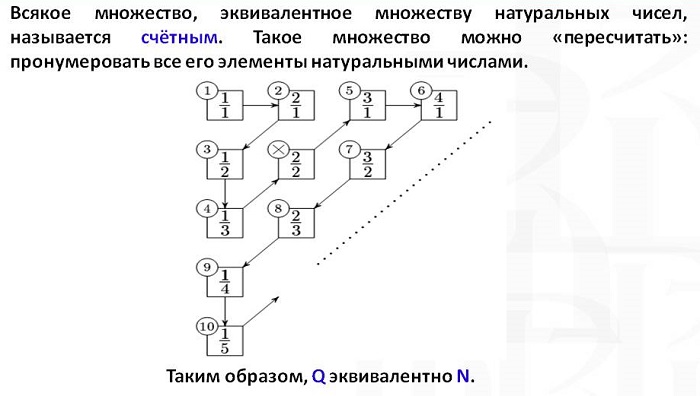
Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник