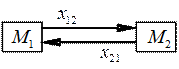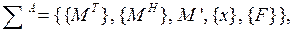Объясните чем различаются статические и динамические модели

Познавательные и прагматичные модели. Статические и динамические модели

Познавательные и прагматические модели

Важную роль в организации любой деятельности человека играют познавательные и прагматичные модели. В силу этого все виды деятельности можно и даже удобно поделить по направленности основного потока информации, который циркулирует между субъектом и окружающем миром. Классифицируются модели в зависимости от того, какую они имеют цель: теоретическую или практическую. Но нужно иметь в виду, что данное деление носит весьма относительный характер и всегда возможно привести некоторые примеры, когда определённую модель просто невозможно отнести к одному из классов. Но и полностью условным такое деление тоже нельзя назвать, поскольку оно отображает реальные различия.

Проявляются подобные различия по-разному. Но чётче всего из различия видны в отношении к оригиналу в процессе деятельности. Только такая ситуация отражает явную разницу между познавательными и прагматическими моделями.

Познавательные модели – это форма организации и представления знаний, которая представляет собой средство соединения новых знаний и имеющихся.

Именно поэтому в ситуации, когда обнаруживаются расхождения между моделью и реальностью возникает вопрос об устранении данного расхождения посредством изменения модели.

Прагматические модели – это средство управления,. Организации практических действий, способ представления требуемых действий или их результата, которые представляют собой рабочее представление цепей.

Из-за чего использование прагматических моделей базируется на обнаружении расхождений между моделью и реальностью направить усилия на изменения реальности таким образом, чтобы максимально приблизить реальность к модели. Исходя из всего этого, можно сделать вывод, что прагматические модели имею нормативный характер, выполняя роль стандарта или образца, чтобы в последствии подогнать под него всю деятельность и её результат. В качестве примера прагматической модели могут выступать программы действий, уставы организаций, кодексы законов, алгоритмы, рабочие чертежи и шаблоны, параметры отбора, технологические допуски, экзаменационные требования и т.п.

Таким образом, можно говорить о том, что основное отличие между познавательными и прагматические моделями, состоит в том, что познавательные модели отражают существующее, а прагматические отражают то, чего не существует, но оно осуществимо и даже желаемо.

Важно отметить, что не стоит воспринимать всё сказанное как абсолютное утверждение.

Иногда возникают сложности с отнесением эстетических моделей или моделей медицины. Также это касается детских игрушек или карт местности. Иногда бывает просто невозможно перечисленные модели отнести к одному из указанных классов.

Под другим углом прагматические модели изменяются и развиваются точно так же, как и познавательные, в их динамическом развитии очень много общего, что способствует размытию отличий.

Статические и динамические модели

Существует ещё один принцип классификации, который разделяет модели на статические и динамические. Он одновременно помогает ответить и на другие вопросы, например, что отображается в модели и что может служить делением моделей.

Статические модели – это конкретное состояние объекта.

Иногда статическое состояние модели называют «моментальной фотографией» интересующего объекта. В качестве примера может служить структурная модель системы.

Динамические модели состояния – это состояние, когда возникает необходимость в отображении процесса изменений состояния.

В качестве примера динамического состояния может служить функциональная модель системы.

Источник

Статические и динамические модели

Под статической экономической системой понимается такая система, координаты которой на изучаемом отрезке времени могут рассматриваться как постоянные. Соответственно, при формулировке статической экономико-математической модеи предполагается, что все зависимости относятся к одному моменту времени, а моделируемая система неизменна во времени. В данном случае игнорируются возможные изменения, т.к. их учет не требуется для достижения цели моделирования. Кроме того, предполагается, что все интересующие процессы, происходящие в системе не требуют при своем описании развертывания во времени.

Поскольку статические модели не содержат фактор времени, то они проще, чем динамические. Поэтому для экономико-математического моделирования типична ситуация, когда сначала разрабатываются статические модели, а затем они усложняются введением фактора времени, т.ею преобразуются в динамические.

В статичных моделях можно выделить группу макроэкономических моделей. К ним относятся модели народно-хозяйственного уровня, которые предназначаются для описания больших секторов экономики или экономики страны в целом. Целью макроэкономического моделирования является изучение экономических законов, связывающих наиболее важные и содержательные показатели.

В целом, разработанные математические модели народного хозяйства можно условно разбить на две большие группы:

· модели экономического роста (часто это динамические модели);

· межотраслевые балансовые модели.

Модели экономического роста оперируют крупноагрегированными показателями (валовой общественный продукт, национальный доход, объем основных фондов, фонд накопления, фонд потребления). Данные модели предназначены для изучения основных тенденций развития экономики в течение продолжительных периодов времени.

Вторая большая группа моделей народного хозяйства –это матричные модели, отображающие соотношения между затратами на производство и его результатами. Матричные модели применяются в межотраслевом балансе, при решении отраслевых задач оптимального планирования развития и размещения производства, в эколого-экономическом моделировании и т. д.

К статическим моделям относится большинство задач линейного программирования (максимизации выпуска в заданном ассортименте, задача о диете, об оптимальных назначениях, раскроя материалов и многие другие).

Под динамической системой понимается всякая система, изменяющаяся во времемни.

Математически это принято выражать через переменные, которые часто называются координатами. Процесс изменения переменных характеризуется траекторией:

,

где координаты 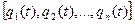являются функциями времени t.

Среди таких систем наиболее простыми являются линейные динамические системы, в которых связи между входными величинами, параметрами состояния и выходными величинами носят характер линейных зависимостей. Существуют два принципиальных подхода к построению таких моделей. Первый подход – оптимизационный, состоит в выборе такой траектории экономического развития из числа возможных, при которой обеспечивается максимальный рост одного или нескольких показателей. Второй подход заключается в исследовании равновесия в экономической системе. В этом случае, переходя к экономической динамике, используют понятие «равновесная траектория», т. е. уравновешенный сбалансированный рост.

В общем виде динамическая модель должна содержать:

· начальное состояние экономического объекта;

· технологические способы производства (каждый способ содержит рецепт получения из заданного набора ресурсов определенного количества продуктов);

· критерий оптимальности (для первого подхода).

Математическое описание динамических моделей производится, как правило:

· системами дифференциальных уравнений (где время выступает в качестве непрерывной переменной);

· разностными уравнениями (где время – дискретная величина);

· системами обыкновенных алгебраических уравнений.

С помощью динамических моделей, в частности, решаются задачи планирования и прогнозирования экономических процессов:

· определения траектории развития экономической системы и ее состояний в заданные моменты времени;

· анализа экономической системы на устойчивость;

Источник

Информатика. 11 класс

Тезаурус

Модель — это объект, который обладает существенными свойствами другого объекта, процесса или явления.

Моделирование — это создание и исследование моделей с целью изучения оригиналов.

Информационные модели — это информация о свойствах оригинала и его связях с внешним миром.

Статические модели — это модели, предполагающие, что интересующие нас свойства не изменяются со временем.

Динамические модели описывают движение, развитие, изменение.

Дискретные модели описывают поведение оригинала в отдельные моменты времени.

Непрерывные модели описывают поведение оригинала для всех моментах времени из некоторого временного промежутка.

Детерминированные модели описываются жестко заданными связями между исходными данными и результатом.

Стохастические модели учитывают случайные события.

Граф — это множество элементов (вершин графа) вместе с набором отношений между ними.

Ребро графа — это линия, соединяющая вершины графа.

Дуга графа — это линия, соединяющая вершины графа и имеющая направление.

Стек — это последовательность, в которой включение и исключение списка происходит с одной стороны.

Очередь — это последовательность, в которой исключение и включение происходит с разных сторон.

Список литературы

Основная литература по теме урока:

Дополнительная литература по теме урока:

Открытые электронные ресурсы по теме:

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§13. Модели и моделирование.

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§13. Модели и моделирование.

Что такое модель?

Ключевые слова:

При слове «модель» у многих, наверное, появляется мысль о моделях самолётов, кораблей, танков и другой техники, которые стоят на полках магазинов. Однако слово «модель» имеет более широкое значение. Например, игрушки, в которые играют дети всех возрастов, — это модели реальных объектов, с которыми они сталкиваются в жизни (или столкнутся в будущем).

Говоря о модели, мы всегда указываем на какой-то другой объект (процесс, явление), например: «Глобус — это модель Земли». Здесь другой объект — это Земля, он называется оригиналом. Объект становится моделью только тогда, когда есть оригинал, модели без оригинала не существует.

Зачем вообще нужны модели? Они появляются тогда, когда мы хотим решить какую-то задачу, связанную с оригиналом, а изучать оригинал трудно или даже невозможно:

• оригинал не существует; например, учебники истории — это модели общества, которого уже нет; возможные последствия ядерной войны учёные изучали на моделях, потому что ставить реальный эксперимент было бы безумием;
• исследование оригинала дорого или опасно для жизни, например, при управлении ядерным реактором, испытании скафандра для космонавтов, создании нового самолёта или корабля;
• оригинал сложно или невозможно исследовать непосредственно, например Солнечную систему, молекулы и атомы, очень быстрые процессы в двигателях внутреннего сгорания, очень медленные движения материков;
• нас интересуют только некоторые свойства оригинала; например, чтобы испытать новую краску для самолёта, не нужно строить самолёт.

Итак, модель всегда связана не только с оригиналом, но и с конкретной задачей, которую мы хотим решить с помощью модели.

Вместе с тем одна и та же модель может описывать множество самых разных оригиналов. Например, в различных задачах атом, муха, человек, автомобиль, высотное здание, даже планета Земля могут быть представлены как материальные точки (если размеры соседних объектов и расстояния между ними значительно больше).

Модель — это объект, который обладает существенными свойствами другого объекта или процесса (оригинала) и используется вместо него.

Назовите свойства самолёта, существенные с точки зрения:

а) конструктора;
б) дизайнера;
в) экономиста;
г) лётчика;
д) бортпроводника;
е) пассажира.

Практически всё, что мы делаем с помощью компьютеров, — это моделирование. Например, база данных библиотеки — это модель реального хранилища книг, компьютерный чертёж — это модель детали и т.д.

Моделирование — это создание и исследование моделей для изучения оригиналов.

С помощью моделирования можно решать задачи четырёх типов:

• изучение оригинала (в научных и учебных целях);
• анализ («что будет, если …») — прогнозирование влияния различных воздействий на оригинал;
• синтез («как сделать, чтобы …») — управление оригиналом;
• оптимизация («как сделать лучше всего …») — выбор наилучшего решения в данных условиях.

Назовите задачи, которые решаются в каждом случае.

а) Даниил считает, как купить новый планшетный компьютер по минимальной цене.
б) Кирилл выясняет, будет ли плавать в воде кусок пластика.
в) Константин проверяет, выдержит ли верёвка вес альпиниста.
г) Василий хочет сделать такой стол, который выдержит нагрузку в 200 кг.
д) Алёна изучает строение молекулы воды.

Какие бывают модели?

Существует множество классификации моделей, каждая из которых отражает какое-то одно свойство. Универсальной классификации моделей нет.

По своей природе модели делятся на материальные (физические, предметные) и информационные.

Материальные модели «можно потрогать» — это игрушки, уменьшенные копии самолётов и кораблей, чучела животных, учебные модели молекул и т. п.

Информационные модели — это информация о свойствах оригинала и его связях с внешним миром. Среди них выделяют вербальные модели (словесные, мысленные) и знаковые модели, записанные с помощью какого-то формального языка:

• графические (схемы, карты, фотографии, чертежи);
• табличные;
• математические (формулы);
• логические (варианты выбора на основе анализа условий);
• специальные (ноты, химические формулы и т. п.).

Различают статические и динамические модели.

В статических моделях предполагается, что интересующие нас свойства оригинала не изменяются во времени.

Динамические модели описывают движение, развитие, изменение.

Какие из этих моделей статические, а какие — динамические:

а) модель полёта шарика;
б) фотография;
в) видеозапись;
г) история болезни;
д) анализ крови;
е) модель молекулы воды;
ж) модель развития землетрясения;
з) модель вращения Луны вокруг Земли?

Динамические модели могут быть дискретными и непрерывными.

Модель называется дискретной, если она описывает поведение оригинала только в отдельные моменты времени. Например, модель колонии животных определяет их численность один раз в год.

Непрерывная модель описывает поведение оригинала для всех моментов времени из некоторого временного промежутка. Например, формула у = sin х и график этой функции — это непрерывные модели. Так как компьютер работает только с дискретными данными, все компьютерные модели — дискретные.

По характеру связей модели делятся на детерминированные и вероятностные.

В детерминированных моделях связи между исходными данными и результатами жёстко заданы, при одинаковых исходных данных всегда получается один и тот же результат (например, при расчёте по известным формулам).

Вероятностные модели учитывают случайность событий в реальном мире, поэтому при одних и тех же условиях результаты нескольких испытаний модели могут отличаться. К вероятностным относятся модели броуновского движения частиц, полёта самолёта с учётом ветра, движения корабля при морском волнении, поведения человека. В результате эксперимента с такими моделями определяют некоторые средние величины по результатам серии испытаний, например среднюю скорость движения частиц, среднее отклонение корабля от курса и т. п. Несмотря на случайность, эти результаты достаточно стабильны, т. е. мало меняются при повторных испытаниях.

Используя дополнительные источники, выясните, от каких иностранных слов произошли слова «вербальный», «статический», «динамический», «детерминированный».

По материалам параграфа составьте в тетради схемы различных классификаций моделей.

Имитационные модели используются в тех случаях, когда поведение сложной системы нельзя (или крайне трудно) предсказать теоретически, но можно смоделировать её реакцию на внешние условия. Для того чтобы найти оптимальное (самое лучшее) решение задачи, нужно выполнить моделирование при многих возможных вариантах и выбрать наилучший из них. Такой метод часто называют методом проб и ошибок.

Имитационные модели позволяют очень точно описать поведение оригинала, но полученные результаты справедливы только для тех случаев, которые мы моделировали (что случится в других условиях — непонятно). Примеры использования имитационных моделей:

• испытание лекарств на мышах, обезьянах, группах добровольцев;
• модели биологических систем;
• экономические модели управления производством;
• модели систем массового обслуживания (банки, магазины и т. п.). Для понимания работы процессора можно использовать его имитационную модель, которая позволяет вводить команды в определённом формате и выполнять их, и показывает изменение значений регистров (ячеек памяти) процессора. Подобные модели применяют в том случае, когда нужно написать программу для системы, на которой её невозможно отлаживать (например, для микропроцессора, встроенного в бытовую технику). Такой подход называют кросс-программированием: программа пишется и отлаживается в одной системе, а работать будет в другой. В этом случае другую систему приходится моделировать с помощью имитационной модели.

Игровые модели позволяют учитывать действия противника, например, при моделировании военных действий, соревнований, конкуренции в бизнесе. Задача игрового моделирования — найти лучшую стратегию в игре — план действий, который даёт наилучшие результаты даже в том случае, когда противник играет безошибочно. Этими вопросами занимается теория игр — раздел математики, одним из создателей которого был американский учёный Джон фон Нейман.

Адекватность моделей

Итак, при моделировании мы заменяем один объект (объект — оригинал) другим. Поэтому всегда возникает вопрос, можно ли верить полученным результатам. Иначе говоря, будет ли оригинал вести себя так же, как и модель?

Адекватность модели — это совпадение существенных свойств модели и оригинала в рассматриваемой задаче.

Используя дополнительные источники, выясните, от какого иностранного слова произошло слово «адекватный».

Адекватность означает, что результаты моделирования:

• не противоречат выводам теории, например законам сохранения (вещества, энергии и т. п.);
• подтверждаются экспериментом с оригиналом.

Таким образом, адекватность модели окончательно можно доказать только экспериментом: если результаты нашего моделирования близки к наблюдаемым на практике, это означает, что модель адекватна.

Для того чтобы вычислить ошибку моделирования, нужно модуль разности между результатом моделирования X и результатом эксперимента X_* разделить на результат эксперимента и умножить на 100%:

Величина «дельта икс» — называется относительной ошибкой. На практике модель обычно считается адекватной, если относительная ошибка не превышает 10%.

Феофан построил математическую модель, которая позволяет прогнозировать изменение веса кошки. Для какого периода времени модель Феофана адекватна?

Нужно понимать, что любая модель отличается от оригинала, поэтому она может быть адекватна только при определённых условиях — в той задаче, для решения которой она создавалась. Например, модель деления амёб (через некоторый интервал времени каждая амёба делится надвое) адекватна только при малом количестве амёб и небольших интервалах наблюдения, иначе амёбы заполнили бы всё пространство.

Во многих случаях результаты моделирования — это некоторые числа, измеренные или рассчитанные по результатам эксперимента с моделью. Это могут быть, например, сила, расстояние, скорость, ускорение, давление и др. Чаще всего эти величины для модели и оригинала будут различаться, поэтому нужно уметь пересчитывать «модельные» данные в соответствующие значения для оригинала. Этими вопросами занимается теория подобия. Простейший пример — работа с картой. Расстояние, измеренное по карте, нужно умножить на масштабный множитель, тогда получится соответствующее расстояние на реальной местности.

Выводы

• Модель — это объект, который обладает существенными свойствами другого объекта, процесса или явления (оригинала) и используется вместо него.

• Моделирование — это создание и исследование моделей для изучения оригиналов.

• С помощью моделирования можно решать задачи четырёх типов:

1) изучение оригинала;
2) анализ — прогнозирование влияния различных воздействий на оригинал;
3) синтез — управление оригиналом;
4) оптимизация — выбор наилучшего решения в данных условиях.

• Универсальной классификации моделей нет. По своей природе модели делятся на материальные и информационные.

• Адекватность модели — это совпадение существенных свойств модели и оригинала в рассматриваемой задаче. Проверить адекватность можно только путём эксперимента с оригиналом.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Что вы думаете по поводу другого определения модели: «Модель — это упрощённое представление реального объекта, процесса или явления»?
2. Приведите примеры разных моделей человека. Для решения каких задач они предназначены?
3. Приведите примеры моделей, с которыми мы работаем на компьютерах.
4. К какому типу (типам) можно отнести следующие модели?

Используйте разные классификации.

5. Какую модель — вероятностную или детерминированную — вы рекомендуете выбрать для исследования движения судна в шторм? Почему?
6. Сравните достоинства и недостатки имитационных и теоретических моделей (например, записанных в виде формул).
7. Верно ли, что модели, используемые при создании компьютерных игр, это игровые модели? Обоснуйте вашу точку зрения.
8. Как можно доказать, что модель неадекватна?
9. Почему ни одна модель не может быть полностью адекватна оригиналу?
10. Выполните по указанию учителя задания в рабочей тетради.

Подготовьте сообщение

а) «Анализ и синтез»
б) «Детерминированные и вероятностные модели»
в) «Игровые модели»
г) «Адекватность моделей»

Источник

Статические и динамические модели

Дата добавления: 2013-12-23 ; просмотров: 19315 ; Нарушение авторских прав

Модель называется статической, когда входные и выходные воздействия постоянны во времени. Статическая модель описывает установившийся режим.

Модель называется динамической, если входные и выходные переменные изменяются во времени. Динамическая модель описывает неустановившийся режим работы изучаемого объекта.

Исследование динамических свойств объектов позволяет в соответствии с фундаментальным принципом определенности Гюйгенса-Адамара ответить на вопрос: как изменяется состояние объекта при известных воздействиях на него и заданном начальном состоянии.

Примером статической модели является зависимость длительности технологической операции от затрат ресурсов. Статическая модель описывается алгебраическим уравнением

.

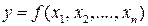
Примером динамической модели является зависимость объемов выпуска товарной продукции предприятия от размеров и сроков капитальных вложений, а также затраченных ресурсов.

Динамическая модель часто описывается дифференциальным уравнением

.

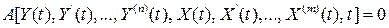
Уравнение связывает неизвестную переменную Y и ее производные с независимой переменной t и заданной функцией времени Х(t) и ее производными.

Динамическая система может функционировать в непрерывном или дискретном, квантованном на равные интервалы, времени. В первом случае система описывается дифференциальным уравнением, а во втором случае – конечно-разностным уравнением.

Если множества входных, выходных переменных и моментов времени конечны, то система описывается конечным автоматом.

Конечный автомат характеризуется конечным множеством состояний входа ; конечным множеством состояний ; конечным множеством внутренних состояний ; функцией переходов T(x, q), определяющих порядок смены внутренних состояний; функцией выходов P(x, q) задающей состояние выхода в зависимости от состояния входа и внутреннего состояния.

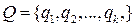
Обобщением детерминированных автоматов являются стохастические автоматы, которые характеризуются вероятностями переходов из одного состояния в другое. Если функционирование динамической системы имеет характер обслуживания возникающих заявок, то модель системы строится с использованием методов теории массового обслуживания.

Динамическую модель называют стационарной, если свойства преобразования входных переменных не изменяются со временем. В противном случае ее называют нестационарной.

Объект может считаться стационарным, если его параметры меняются медленно по сравнению со временем, которое требуется для идентификации объекта.

Различают детерминированные и стохастические (вероятностные) модели. Детерминированный оператор позволяет однозначно определить выходные переменные по известным входным переменным.

Детерминированность модели означает лишь неслучайность преобразования входных переменных, которые сами по себе могут быть как детерминированными, так и случайными.

Стохастический оператор позволяет определить по заданному распределению вероятностей входных переменных и параметров системы распределение вероятностей входных переменных.

С точки зрения входных и выходных переменных модели классифицируют следующим образом:

1. Входные переменные подразделяют на управляемые и неуправляемые. Первые могут изменяться по усмотрению исследователя и используются объектом. Вторые непригодны для управления.

2. В зависимости от размерности векторов входных и выходных переменных различают одномерные и многомерные модели. Под одномерной моделью будем понимать такую модель, у которой входная и выходная переменные являются одновременно скалярными величинами. Многомерной называют модель, у которой векторы x(t) и y(t) имеют размерность n ³ 2.

3. Модели, у которых входныеи выходные переменные являются непрерывными по времени и по величине, называют непрерывными. Модели, у которых входные и выходные переменные дискретны или по времени, или по величине, называют дискретными.

Отметим, что динамика сложных систем во многом зависит от решений, принимаемых человеком. Процессы, протекающие в сложных системах, характеризуются большим числом параметров – большим в том смысле, что соответствующие уравнения и соотношения аналитически не могут быть разрешены. Часто изучаемые сложные системы уникальны по сравнению даже с аналогичными по назначению системами. Продолжительность экспериментов с такими системами обычно велика и часто оказывается сравнимой со сроком их жизни. Иногда проведение активных экспериментов с системой вообще недопустимо.

Для сложного объекта часто оказывается невозможным определить содержание каждого шага управления. Это обстоятельство определяет настолько большое число ситуаций, характеризующих состояние объекта, что практически невозможно проанализировать влияние каждой из них на принимаемые решения. В этой ситуации вместо жесткого алгоритма управления, предписывающего на каждом шаге его реализации некоторое однозначное решение, приходится использовать совокупность указаний, соответствующую тому, что в математике принято называть исчислением. В отличие от алгоритма в исчислении продолжение процесса на каждом шаге не является фиксированным и есть возможность произвольного продолжения процесса поиска решения. Исчисления и подобные им системы изучаются в математической логике.

1.5. Концепция построения системной модели сложных объектов

Сложные объекты представляют собой совокупность отдельных конструктивно обособленных элементов: технологических агрегатов, транспортных магистралей, электрических приводов и т. д., связанных между собой материальными, энергетическими и информационными потоками, и взаимодействующих с окружающей средой как целое. Процессы энергомассообмена, происходящие в сложных объектах, являются направленными и связаны с движением полей и вещества (теплообмен, фильтрация, диффузия, деформация и т. д.). Как правило, эти процессы содержат неустойчивые стадии развития, и управление такими процессами является больше искусством, чем наукой. Вследствие этих обстоятельств, наблюдается нестабильное качество управления такими объектами. Резко возрастают требования к квалификации технологического персонала и существенно увеличивается время на его подготовку.

Элементом системы называется некоторый объект (материальный, энергетический, информационный), обладающий рядом важных для нас свойств, внутреннее строение (содержание) которого не представляет интереса с точки зрения цели анализа [15].

Будем обозначать элементы через М, а всю их рассматриваемую (возможную) совокупность – через . Принадлежность элемента к совокупности принято записывать .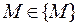

Связью назовем важный для целей рассмотрения обмен между элементами: веществом, энергией, информацией.

Единичным актом связи выступает воздействие. Обозначая все воздействия элемента M₁ на элемент M₂ через x₁₂, а элемента М₂ на М₁ – через x₂₁, можно изобразить связь графически (рис. 1.6).

Рис. 1.6. Связь двух элементов

Системой назовем совокупность элементов, обладающую следующими признаками:

а) связями, которые позволяют посредством переходов по ним от элемента к элементу соединить два любых элемента совокупности;

б) свойством (назначением, функцией), отличным от свойств отдельных элементов совокупности.

Назовем признак а) связностью системы, б) – ее функцией. Применяя так называемое “кортежное” (т. е. последовательность в виде перечисления) определение системы, можно записать

,

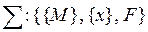
где Σ– система; <М> – совокупность элементов в ней; <x> – совокупность связей; F – функция (новое свойство) системы.

Будем рассматривать запись как наиболее простое описание системы.

Практически любой объект с определенной точки зрения может рассматриваться как система. Важно отдавать себе отчет, полезен ли такой взгляд или разумней считать данный объект элементом. Так, системой можно считать радиотехническую плату, преобразующую входной сигнал в выходной. Для специалиста по элементной базе системой будет слюдяной конденсатор в этой плате, а для геолога – и сама слюда, имеющая достаточно сложное строение.

Большой системой назовем систему, включающую значительное число однотипных элементов и однотипных связей.

Сложной системой назовем систему, состоящую из элементов разных типов и обладающую разнородными связями между ними.

Часто сложной системой считают только ту, которая является большой. Разнородность элементов можно подчеркнуть записью

.

Большой, но не сложной с точки зрения механики, системой является собранная из стержней стрела крана или, например, труба газопровода. Элементами последней будут ее участки междусварными швами или опорами. Для расчетов на прогиб элементами газопровода скорее всего будут считаться относительно небольшие (порядка метра) участки трубы. Так поступают в известном методе конечных элементов. Связь в данном случае носит силовой (энергетический) характер – каждый элемент действует на соседний.

Различие между системой, большой системой и сложной системой условно. Так, корпуса ракет или судов, которые на первый взгляд однородны, обычно относят к сложной системе из-за наличия переборок разного вида.

Важным классом сложных систем являются автоматизированные системы. Слово “автоматизированный” указывает на участие человека, использование его активности внутри системы при сохранении значительной роли технических средств. Так, цех, участок, сборка могут быть как автоматизированными, так и автоматическими (“цех-автомат”). Для сложной системы автоматизированный режим считается более предпочтительным. Например, посадка самолета выполняется при участии человека, а автопилот обычно используется лишь на относительно простых движениях. Также типична ситуации, когда решение, выработанное техническими средствами, утверждается к исполнению человеком.

Итак, автоматизированной системой называется сложная система с определяющей ролью элементов двух типов: а) в виде технических средств; б) в виде действий человека. Ее символьная запись (сравни с и )

где M T – технические средства, в первую очередь ЭВМ; M H – решения и другая активность человека; М’ – остальные элементы в системе.

Структурой системы называется ее расчленение на группы элементов с указанием связей между ними, неизменное на все время рассмотрения и дающее представление о системе в целом.

Указанное расчленение может иметь материальную (вещественную), функциональную, алгоритмическую и другую основу. Группы элементов в структуре обычно выделяются по принципу простых или относительно более слабых связей между элементами разных групп. Структуру системы удобно изображать в виде графической схемы, состоящей из ячеек (групп) и соединявших их линий (связей). Такие схемы называются структурными.

Для символьной записи структуры введем вместо совокупности элементов <М>,совокупность групп элементов <М*>и совокупность связей между этими группами <x*>.Тогда структура системы может быть записана как

.

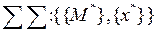
Структуру можно получить из объединением элементов в группы. Отметим, что функция (назначение) F системы в опущена.

Приведем примеры структур. Вещественная структура сборного моста состоит из его отдельных, собираемых на месте секций. Грубая структурная схема такой системы укажет только эти секции и порядок их соединения. Последнее и есть связи, которые здесь носят силовой характер. Пример функциональной структуры – это деление двигателя внутреннего сгорания на системы питания, смазки, охлаждения, передачи силового момента и т. д. Пример системы, где вещественные и функциональные структуры слиты, – это отделы проектного института, занимающиеся разными сторонами одной и той же проблемы.

Типичной алгоритмической структурой будет алгоритм (схема) программного средства, указывающая последовательность действий. Также алгоритмической структурой будет инструкция, определяющая действия при отыскании неисправности технического объекта.

1.6. Основные этапы инженерного эксперимента, направленного на изучение сложных объектов

Дадим характеристику основных этапов инженерного эксперимента, направленного на изучение сложных объектов.

1. Построение физической основы модели.

Построение физической основы модели, позволяющей выделить наиболее существенные процессы, определяющие качество управления и определить соотношения детерминированных и статистических составляющих в наблюдаемых процессах. Физическая основа модели строится с использованием “проектирования” сложного объекта в различные предметные области, используемые для описания исследуемого объекта. Каждая предметная область задает собственные системы ограничений на возможные “движения” объекта. Учет совокупности этих ограничений позволяет обосновать комплекс используемых моделей и построить непротиворечивую модель.

Построение “каркаса” модели, т. е. ее физической основы, сводится к описанию системы отношений, характеризующих исследуемый объект, в частности, законов сохранения и кинетики процессов. Анализ системы отношений, характеризующих объект, позволяет определить пространственные и временные масштабы механизмов, инициирующих наблюдаемое поведение процессов, качественно охарактеризовать вклад статистического элемента в описание процесса, а также выявить принципиальную неоднородность (если она существует!) наблюдаемых временных рядов.

Построение “каркаса” сводится к установлению по априорным данным причинно-следственных связей между внешними и внутренними дестабилизирующими факторами и эффективностью работы системы, а количественные оценки этих связей конкретизируются путем проведения экспериментов на объекте. Тем самым гарантируется общность полученных результатов для всего класса объектов, их непротиворечивость по отношению к ранее полученным знаниям и обеспечивается уменьшение объема экспериментальных исследований. “Каркас” модели должен строиться с использованием структурно-феноменологического подхода, объединяющего исследование объекта по его реакциям на “внешние” воздействия и раскрытие внутреннего строения объекта исследования.

2. Проверка статистической устойчивости результатов наблюдений и определение характера изменения контролируемых переменных.

Эмпирическое обоснование статистической устойчивости сводится к исследованию устойчивости эмпирического среднего по мере возрастания объема выборки (схема удлиняющейся серии). Непредсказуемость экспериментально полученных значений, как известно, не является ни необходимым, ни достаточным условием применения теоретико-вероятностных понятий. Необходимым условием применения теории вероятностей является устойчивость усредненных характеристик исходных величин. Таким образом, требуется проверка с использованием эмпирической индукции статистической устойчивости n-мерной эмпирической функции распределения исходной случайной величины и распределения вероятностей для выборочных оценок.

3. Формирование и проверка гипотез о структуре и параметрах “движения” исследуемого объекта.

Отметим, что, как правило, мотивом для выбора статистического подхода является отсутствие регулярности наблюдаемого процесса, хаотический характер и резкие изломы. В этом случае исследователь не может визуально обнаружить закономерности в ряду наблюдений и воспринимает его как реализацию случайного процесса. Подчеркнем, что речь идет об обнаружении простейших закономерностей, поскольку для обнаружения сложных закономерностей нужна направленная математическая обработка результатов наблюдений.

4. Прогнозирование выходных переменных выполняется с учетом вклада детерминированных и статистических составляющих в конечный результат.

Отметим, что использование для прогнозирования только статистического подхода наталкивается на серьезные трудности. Во-первых, для принятия решений, касающихся минимизации текущих потерь, важно знать, не как в среднем развивается процесс, а как он будет себя вести на конкретном отрезке времени. Во-вторых, в общем случае мы имеем задачу прогнозирования нестационарного, случайного процесса с изменяющимися математическим ожиданием, дисперсией и самим видом закона распределения.

5. Планирование и реализация вычислительного эксперимента, направленного на оценку регулировочных характеристик объекта и ожидаемой эффективности системы управления.

Задачи синтеза структуры сложных систем только в простейших случаях могут быть решены аналитически. Поэтому возникает потребность в имитационном моделировании (ИМ) элементов проектируемой системы.

ИМ – это особый способ исследования объектов сложной структуры, заключающийся в воспроизведении численным образом всех входных и выходных переменных каждого элемента объекта. ИМ позволяет на этапе анализа и синтеза структуры учесть не только статистические взаимосвязи между элементами системы, но и динамические аспекты ее функционирования.

Для составления ИМ необходимо:

– выделить в объекте моделирования простейшие элементы, для которых известен способ расчета выходных переменных;

– составить уравнения связи, описывающие порядок соединения элементов в объекте;

– составить структурную схему объекта;

– выбрать средства автоматизации моделирования;

– разработать программу ИМ;

– провести вычислительные эксперименты с целью оценки адекватности ИМ, устойчивости результатов имитации и чувствительности ИМ к изменениям управляющих и возмущающих воздействий;

– решить с использованием модели задачу синтеза системы управления.

Источник