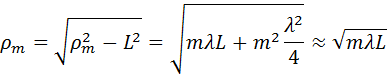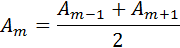Объяснить что такое зона френеля

Что такое зона Френеля и CCQ (Client Connection Quality) или фундаментальные факторы качественного беспроводного моста

Содержание

В данной статье хочу поговорить о фундаментальных факторах построения качественного беспроводного моста, так как многие «сете-строители» считают, что вполне достаточно будет купить качественное сетевое оборудование, установить и получить 100% отдачу от них — что в итоге не у всех получается.

CCQ — что это?

CCQ (Client Connection Quality) с английского переводиться как «качество клиентского соединения» — что в принципе показывает процентное соотношение теоретически возможной к реально текущей пропускной способности канала, иными словами процент достигнутой пропускной способности с максимально возможной на конкретном оборудовании.

К примеру, вы используете оборудование с максимально возможно пропускной способностью в 200 мбит/с, а по факту на текущем канале 100 мбит/с — в таком случае CCQ равен 50%

В сетевом оборудовании Mikrotik и Ubiquiti присутствуют два отдельных индикатора
Tx. CCQ (Transmit CCQ) — скорость передачи данных.
Rx. CCQ (Receive CCQ) — скорость приема данных.

Три основных фактора влияющие на качество CCQ

1. Юстировка двух антенн. Если говорить о беспроводном мосте «точка-точка» то понятно что антенны должны смотреть друг на друга максимально точно, «глаза в глаза».

Если нужен wi-fi мост «точка-многоточка» — то изначально нужно продумать всю архитектуру от секторной антенны провайдера до клиентских, так что бы они пересекались максимально точно.

2. Наличие шума в канале. Перед тем как определиться с частотой wi-fi моста, обязательно проверить каждую частоту на наличие шума, исходя из данной проверки остановиться на менее загруженной частоте.

3. Зона Френеля.

Зона Френеля — что это?

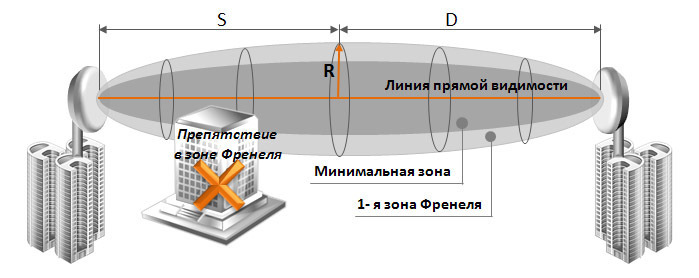
Зона Френеля это объем радио-волнового канала между двумя антеннами.

Максимальный объем канала находиться в центральной точке между двумя антеннами.

Для максимально качественного сигнала нужно подобрать наиболее чистую зону, как от физических препятствий, так и от радио-волновых (о чем говорили во втором пункте).

Как рассчитать зону Френеля?

Формула расчета зоны Френеля в центральной ее точке:

D — расстояние (km)
f — частота (GHz)

Формула расчета зоны Френеля в любой ее точке, например в месте препятствия:

f — частота (GHz)
D1 — расстояние до нужной вам точки расчета, от первой антенны (km)
D2 — расстояние до нужной вам точки расчета, от второй антенны (km)

Хорошенько проработав данные три фактора, вы в итоге получите стабильный беспроводной мост, с максимально возможной скоростью передачи данных.

Источник

Дифракция света

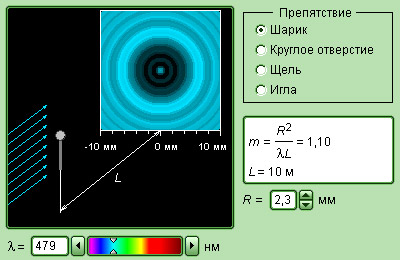
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

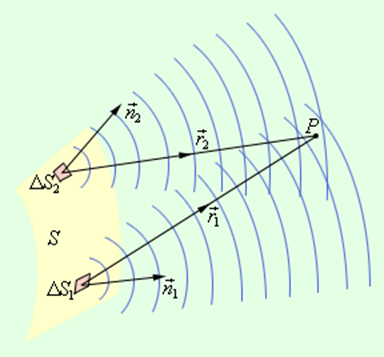
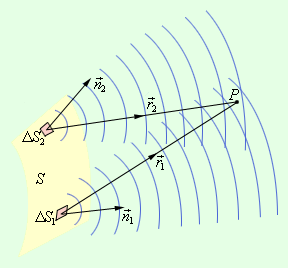
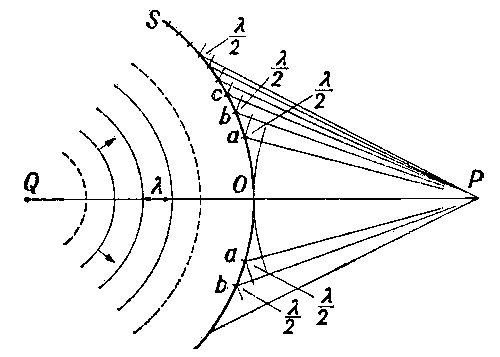
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т.Юнгом. Независимо от него в 1818 г. французский ученый О.Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающих вторичных волнах Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.

Принцип Гюйгенса–Френеля. ΔS₁ и ΔS₂ – элементы волнового фронта, и – нормали

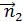
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.

Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS₁, ΔS₂ и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.

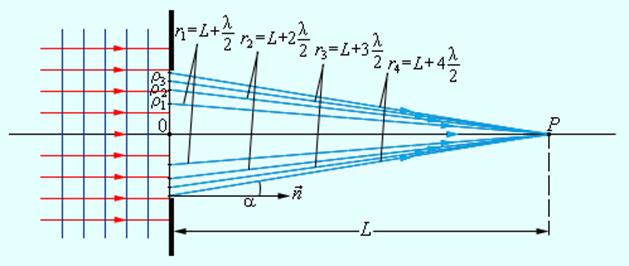
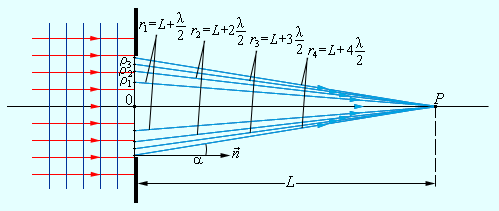
Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).

Дифракция плоской волны на экране с круглым отверстием

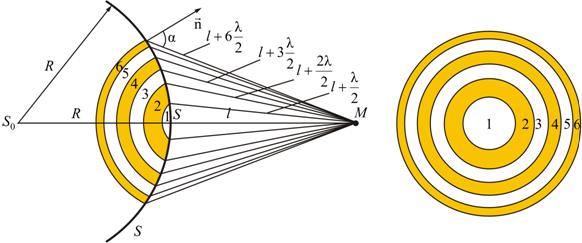
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A₀ падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.

…

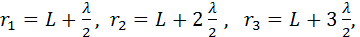
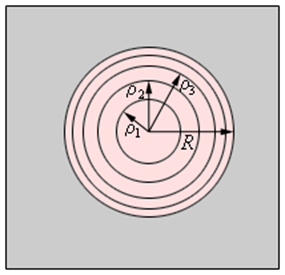
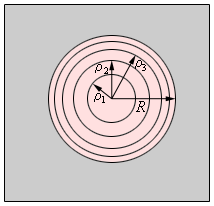
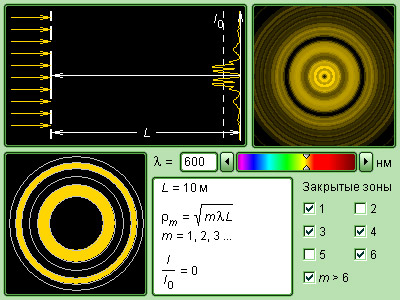
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).

Границы зон Френеля в плоскости отверстия

Из рис. 3.8.2 легко найти радиусы ρm зон Френеля:

где Am – амплитуда колебаний, вызванных m-й зоной.

С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.

Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть

Источник

Зона Френеля

Что такое зона Френеля

Зонами Френеля называют области, на которые можно разделить поверхность световой, либо звуковой волны с целью расчета результатов дифракции света или звука.

Методика анализа была впервые применена О. Френелем в 1815 – 1819 годах. Зону Френеля можно наглядно представить в виде объема радио-волнового канала между двумя передатчиками сигнала.

Максимальное значение объема канала отмечено центральной точкой, равноудаленной от двух антенн. Наиболее качественный сигнал обеспечивается путем подбора максимально чистой зоны, в которой отсутствуют физические и радио-волновые препятствия.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Расчет радиуса зоны Френеля

С помощью определенных характеристик можно выполнить корректный расчет. Для определения зоны Френеля в ее центре необходимо использовать формулу:

Где D равно расстоянию в километрах, f является частотой в GHz.

Если необходимо рассчитать размер зоны Френеля в любой ее точке, к примеру, в месте, где обнаружено препятствие, следует воспользоваться формулой:

Где f — это частота в GHz, D1 является расстоянием от первой антенны до искомой точки в километрах, D2 равно расстоянию от второй антенны до искомой точки в километрах.

Знание характеристик зоны Френеля позволяет выполнить точные расчеты. В практическом применении представленные формулировки обеспечивают данные для стабильности параметров беспроводного моста и максимально возможной скорости передачи сигнала.

Метод зон Френеля, основные принципы работы

С целью упрощения решений задач волновая поверхность S разбивается на отдельные зоны. Данный способ называют методом зон Френеля.

Точки поверхности S, которые являются границей первой или центральной зоны и удалены от точки М на расстояние:

Точки сферы S, которые находятся на расстоянии:

и так далее относительно точки М, образуют 2, 3 и так далее зоны Френеля.

В точке М образуются колебания. Они расположены между двумя соседними зонами, фазы которых противоположны по причине разности ходя от этих зон до точки М:

В процессе сложения колебания друг друга ослабляют:

Где A является амплитудой результирующего колебания, Аi представляет собой амплитуду колебаний, возбуждаемую i-й зоной Френеля.

Значение Аi определяется площадью Si зоны и углом αi между нормалью к поверхности и прямой, направленной в точку M. Расчет площади одной зоны выглядит следующим образом:

Исходя из представленного уравнения, можно сделать вывод о независимости площади зоны Френеля от номера зоны i. Данное утверждение позволяет сделать вывод о том, что при малых числах i соседние зоны будут обладать одинаковыми площадями. В то время, как номер зоны увеличивается, возрастает угол αi, а также снижается интенсивность излучения зоны по направлению к точке М, то есть уменьшается амплитуда Аi. Другой причиной данного явления служит увеличение расстояния до точки М: \(x = <-b \pm \sqrt\over 2a>\) В целом количество зон Френеля, которые уменьшаются на части сферы, направленной к точке М, достаточно большое:

если радиус R=l=1 метр,

\(\lambda =-5\times 10^<-7>\) составляет 500 нм.

Количество зон \(N\approx 3\times 10^<5>\)

Радиус первой зоны \(r_<1>\approx 0.16\) мм

Исходя из вышеизложенной информации, можно сделать вывод о равенстве углов соседних зон между нормалью к зоне и направлением на точку М. Таким образом, наблюдается примерное равенство амплитуд волн, которые приходят в точку М от соседних волн. При прямолинейном распространении световой волны фазы колебаний, которые образованы в соседних зонах, будут отличаться на π. Согласно этим данным, в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны рассчитывается, как среднее арифметическое от амплитуд зон, которые к ней примыкают:

В таком случае, исходное уравнение можно преобразовать следующим образом:

Из равенства площадей, которыми обладают соседние зоны, вытекает нулевое значение выражения, заключенного в скобках. Тогда результирующая амплитуда будет равна:

Расчет интенсивности излучения имеет вид:

Таким образом, результирующая амплитуда, которая образована в какой-либо точке М всей сферической поверхностью, определяется, как половина амплитуды, сформированной одной лишь центральной областью, а интенсивность составляет:

Радиус, которым характеризуется центральная зона, небольшой:

Тогда допустимо считать распространение света от точки Р до точки М прямолинейным. В условиях, когда путь волны преграждает непрозрачный экран, в котором есть отверстие, открывающее только центральную зону Френеля, то амплитуда в точке М составляет А1. Поэтому, интенсивность в точке М превышает в 4 раза тот же показатель, но в условиях без экрана. В случае, когда все зоны с четными номерами закрыты, интенсивность света будет увеличиваться.

Таким образом, объясняют прямолинейность распространения света в условиях однородной среды с помощью принципа Гюйгенса-Френеля. Справедливость деления волнового фронта на зоны Френеля нашла подтверждение в ходе эксперимента. Для опыта используют зонные пластинки, представляющие собой систему чередующихся прозрачных и непрозрачных колец. Эксперимент подтверждает возможность увеличения освещенности в точке М с помощью зонных пластинок по принципу собирающей линзы.

Принцип Гюйгенса-Френеля

Дифракцией света в наиболее распространенном понятии называют огибание световыми лучами границы непрозрачных тел или экранов, то есть проникновение света в область с геометрической тенью.

Максимально рельефно дифракцию света можно наблюдать в зонах с резким изменением плотности потока лучей:

Дифракция волн тесно связана с процессами, при которых волны распространяются и рассеиваются в неоднородных средах.

Дифракция — это комплекс явлений, которые можно наблюдать в процессе распространения света в среде, отличающейся резкими неоднородностями, габариты которых соотносимы с длиной волны и связаны с отклонениями от законов геометрической оптики.

Огибание препятствий звуковыми волнами, то есть дифракцию звуковых волн, можно заметить в повседневной жизни.

К примеру, за углом дома слышен звук. Для того чтобы наблюдать дифракцию световых лучей, требуются специальные условия, что является причиной небольшой длины световых волн. Интерференция не отличается существенно от дифракции. Данные явления зависят от перераспределения светового потока в результате суперпозиции волн.

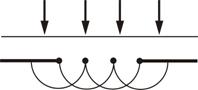
Дифракция объясняется принципом Гюйгенса. Согласно данному утверждению, каждая точка, которую достигает волна, является центром вторичных волн, а огибающая этих волн определяет положение волнового фронта в следующий момент времени.

На рисунке изображен непрозрачный экран, на отверстие в котором нормально падает плоская волна.

Каждая точка области волнового фронта, выделенного отверстием, представляет собой источник вторичных волн. В условиях однородной среды они будут иметь сферическую форму. С помощью огибающих вторичных волн для некоторого момента времени можно увидеть, что фронт волны достигает области геометрической тени, то есть волна огибает края отверстия.

Благодаря принципу Гюйгенса, можно решить задачу, связанную с направлением, в котором распространяется волновой фронт. Но утверждение не касается вопроса о таких характеристиках разнонаправленных волн, как амплитуда и интенсивность. Решающая роль в определении волновой природы света отведена О. Френелю, который проводил данные исследования в начале XIX века. Ученый представил объяснение явлению дифракции и ее количественный расчет. В 1818 году Френель был удостоен премии Парижской академии за достижения в данной области.

Френель дополнил принцип Гюйгенса физическим смыслом с помощью идеи интерференции вторичных волн. Ученый рассматривал дифракцию по средствам нескольких ключевых положений, которые не требую доказательств. Комплекс данных утверждений называют принципом Гюйгенса-Френеля. Исходя из принципа Гюйгенса, каждая точка фронта волны рассматривается в качестве источника вторичных волн. Френель значительно развил это утверждение:

Благодаря данным положениям, Френелю удалось составить дифракционную картину. Используя справедливые утверждения, ученый выполнял количественные расчеты, характеризующие явление дифракции.

Источник

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.

Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.

Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.

Принцип Гюйгенса-Френеля

Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.

Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.

Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.

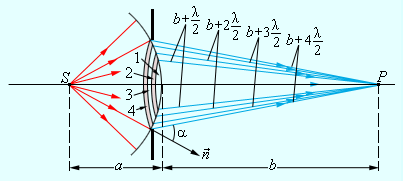
Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.

Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.

Зоны Френеля. Интерференционный максимум

Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:

Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.

Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.

Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:

Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.

Получим формулы вида:

Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:

Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.

Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.

При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как

Выводы по теории Френеля справедливы.

Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.

Источник

Зоны Френеля

Полезное

Смотреть что такое «Зоны Френеля» в других словарях:

ЗОНЫ ФРЕНЕЛЯ — участки, на к рые разбивают поверхность фронта световой волны для упрощения вычислений при определении амплитуды волны в заданной точке пр ва. Метод З. Ф. используется при рассмотрении задач о дифракции волн в соответствии с Гюйгенса Френеля… … Физическая энциклопедия

ФРЕНЕЛЯ — (1) дифракция (см.) сферической световой волны, при рассмотрении которой нельзя пренебречь кривизной поверхности падающей и дифрагировавшей (либо только дифрагировавшей) волн. В центре дифракционной картины от круглого непрозрачного диска всегда… … Большая политехническая энциклопедия

ФРЕНЕЛЯ ЗОНЫ — участки, на которые разбивается волновая поверхность при рассмотрении дифракционных волн (Гюйгенса Френеля принцип). Зоны Френеля выбираются так, чтобы удаление каждой следующей зоны от точки наблюдения было на половину длины волны больше, чем… … Большой Энциклопедический словарь

Френеля зоны — участки, на которые разбивают волновую поверхность при рассмотрении дифракции волн (Гюйгенса Френеля принцип). Зоны Френеля выбираются так, чтобы удаление каждой следующей зоны от точки наблюдения было на половину длины волны больше, чем удаление … Энциклопедический словарь

Френеля дифракция — дифракция сферической световой волны на неоднородности (например, отверстии), размер которой сравним с диаметром одной из зон Френеля (См. Зоны Френеля). Название дано в честь изучившего этот вид дифракции О. Ж. Френеля (См. Френель).… … Большая советская энциклопедия

ФРЕНЕЛЯ ЗОНЫ — участки, на к рые разбивают поверхность фронта световой волны для упрощения вычислений при определении амплитуды волны в заданной точке про странства. Метод Ф. з. используется при рассмотрении задач о дифракции волн в соответствии с Гюйгенса… … Физическая энциклопедия

ФРЕНЕЛЯ ЗОНЫ — участки, на к рые разбивают волновую поверхность при рассмотрении дифракции волн (Гюйгенса Френеля принцип). Ф. з. выбираются так, чтобы удаление каждой след. зоны от точки наблюдения было на половину длины волны больше, чем удаление предыдущей… … Естествознание. Энциклопедический словарь

Источник