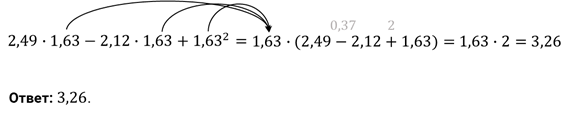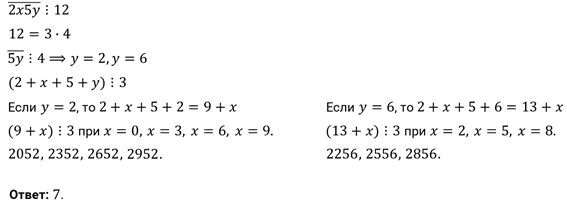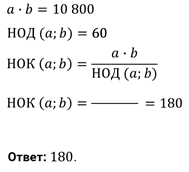Общее свойство чисел что это такое в математике

Свойства чисел

Ниже приведены характеристики чисел с примерами, которые рассматривает сайт aboutnumber.ru

Сумма цифр

Сумма цифр, из которых состоит число.

Произведение цифр

Произведение цифр, из которых состоит число.

Количество цифр в числе

Отображение количества цифр в числе (если их больше 4-х). Это удобно, так как не всегда можно на глаз определить порядок числа.

Все делители числа

Полный список делителей, на которые делится число без остатка.

Наибольший делитель из ряда степеней двойки

Ряд степеней двойки — это ряд вида 1, 2, 4, 8, 16, 32, 64, 128, 256 и т.д. Эти числа являются основными числами в бинарной математике (в двоичной записи), так как ими можно охарактеризовать объем информации.

Количество делителей

Суммарное число делителей.

3638143886 → всего 32 делителя

Сумма делителей

Сумма всех делителей числа.

77432243032 → сумма делителей 145185455700

Простое число

Проверка на простое число. Простое число — это число, которое делится без остатка только на единицу и само себя. Таким образом у простого числа может быть всего два делителя.

Полупростое число

Проверка на полупростое число. Полупростое число — число, которое можно представить в виде произведения двух простых чисел. У полупростого числа два делителя — оба простые числа.

Обратное число

Два числа называются обратными если их произведение равно единице. Таким образом обратным к заданному числу N всегда будет 1/N.

Проверка: 0.008 * 125 = 1

Факторизация

Факторизация числа — представление числа в виде произведения простых чисел.

Двоичный вид

Двоичное, оно же бинарное представление числа. Это запись числа в системе счисления с основанием два.

Троичный вид

Троичное представление числа. Это запись числа в системе счисления с основанием три.

Восьмеричный вид

Восьмеричное представление числа. Это запись числа в системе счисления с основанием восемь.

Шестнадцатеричный вид (HEX)

Шестнадцатеричное представление числа. Часто его пишут английскими буквами «HEX». Это запись числа в системе счисления с основанием шестнадцать.

Перевод из байтов

Конвертация из байтов в килобайты, мегабайты, гигабайты и терабайты.

29141537 (байт) → 27 мегабайтов 810 килобайтов 545 байтов

В случаем, если число меньше чем 16777216, то его можно представить в виде цвета. Шестнадцать миллионов цветов, которые можно закодировать стандартной цветовой схемой компьютера.

RGB(126, 141, 204) или #7E8DCC

Наибольшая цифра в числе (возможное основание)

Наибольшая цифра, встречающаяся в числе. В скобках указана система счисления, с помощью которой, возможно, записано это число.

347524172 → 7 (8, восьмеричный вид)

Перевод двоичной/троичной/восьмеричной записи в десятичную

Число, записанное с помощью единиц и нолей — имеет бинарный вид, таким образом его можно перевести в десятичную систему счисления.

Число, записанное с помощью единиц, нолей и двоек — имеет троичный вид.

Если с помощью цифр до семи (включая) — восьмеричный вид числа.

Число Фибоначчи

Проверка на число Фибоначчи. Числа Фибоначчи — это последовательно чисел, в которых каждый последующий элемент равен сумме двух предыдущих.

Ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.

Позиция в ряду Фиббоначчи

Характеризует порядковый номер числа в ряду Фибоначчи.

21 → 8-е число в ряду Фибоначчи

Нумерологическое значение

Нумерологическое значение вычисляется путем последовательного сложения всех цифр числа до тех пор, пока не не получится цифра от 0 до 9. В нумерологии каждой цифре соответствует свой характер.

8372890 → 8 + 3 + 7 + 2 + 8 + 9 + 0 = 37 → 3 + 7 = 10 → 1 + 0 =

1 мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательность

Синус числа

Расчет тригонометрической функции синуса числа в радианах.

Косинус числа

Расчет тригонометрической функции косинуса числа в радианах.

Тангенс числа

Расчет тригонометрической функции тангенса числа в радианах. Чтобы получить котангенс числа, надо единицу поделить на величину тангенса.

Натуральный логарифм

Это логарифм числа по основанию константы e ≅ 2,718281828459.

Десятичный логарифм

Это логарифм числа по основания десять.

Квадратный корень

Квадратный корень из введенного числа.

Кубический корень

Кубический корень из введенного числа.

Квадрат числа

Число, возведенное в квадрат, то есть умноженное само на себя.

Перевод из секунд

Конвертация числа секунд в дни, часы, минуты и секунды.

1805506 (секунд) → 2 недели 6 дней 21 час 31 минута 46 секунд

Дата по UNIX-времени

UNIX-время или UNIX-дата — количество секунд, прошедших с полуночи 1 января 1970 года (по UTC). Таким образом введенное число можно преобразовать в дату.

5265079917115 → Sun, 04 Nov 2136 10:11:57 GMT

Римская запись

Римская запись числа, в том случае, если оно меньше чем максимальное для римской записи 3999.

Индо-арабское написание

Запись числа с помощью индо-арабских цифр. Они используются в арабских странах Азии и в Египте.

Азбука морзе

Число, закодированное с помощью азбуки морзе, каждый символ которой представляется в виде последовательсти коротких (точка) и длинных (тире) сигналов.

Хэш-сумма числа, рассчитанная по алгоритму MD5.

Хэш-сумма числа, рассчитанная по алгоритму SHA-1.

Base64

Представление числа в системе Base64, то есть в системе счисления с основанием 64.

QR-код числа

Двумерный штрих-код-картинка. В ней зашифровано введенное число.

Источник

Натуральные числа и их свойства

Вы будете перенаправлены на Автор24

Натуральные числа и их свойства

Нуль не относят к натуральным числам.

Свойства отношения следования

Единица- натуральное число, которое не следует ни за каким натуральным числом.

За каждым натуральным числом следует одно и только одно число

Свойство сложения натуральных чисел

Сумма не изменяется при перестановке слагаемых

Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом, к полученной сумме- второе слагаемое

От прибавления нуля число не измениться и если прибавить к нулю какое- нибудь число, то получится прибавленное число.

Свойства вычитания

Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а затем из полученной разности- второе слагаемое

Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое

Если из числа вычесть нуль, то число не изменится

Если из числа вычесть его само, то получится нуль

Готовые работы на аналогичную тему

Свойства умножения

Произведение двух чисел не изменяется при перестановке множителей

Чтобы умножить число на произведение двух чисел,можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель

При умножении на нуль произведение равно нулю

Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо

Свойства умножения относительно сложения и вычитания

Распределительное свойство умножения относительно сложения

Для того чтобы умножить сумму на число,можно умножить на это число каждое слагаемое и сложить получившиеся произведения

Распределительное свойство умножение относительно вычитания

Для того,чтобы умножить разность на число,множно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе

Сравнение натуральных чисел

Меньшим считается число, которое в натуральном ряду появляется раньше, а большим, которое появляется позже. Нуль меньше любого натурального числа.

в любом подмножестве натуральных чисел, содержащем хотя бы одно число, есть наименьшее число

Подмножеством в математике называют часть множества. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества

Округление натуральных чисел

Натуральные числа округляют до десятков, сотен,тысяч и т.д

Правило округления натуральных чисел

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 05 2021

Источник

Числа и их свойства

Урок 1. Подготовка к ЕГЭ по математике

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Числа и их свойства»

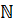
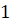
Напомним, что понятие «натуральное число» является первоначальным, неопределяемым. Оно возникло из потребностей счёта. Множество натуральных чисел обозначают . Наименьшее натуральное число — . Наибольшего натурального числа нет. Для записи натуральных чисел используют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Нуль не является натуральным числом.

Число, например, состоящее из а сотен, b десятков и c единиц, записывается в виде:

.

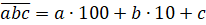
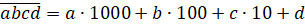
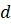
В следующей записи цифра а показывает количество тысяч, b — количество сотен, b — количество десятков и — количество единиц в числе.

Вы уже знаете, что натуральные числа можно сравнивать между собой, складывать и умножать. Из большего натурального числа можно вычесть меньшее.

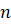
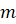
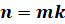
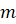
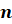
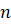
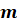
Если натуральное число делится на натуральное число без остатка, то есть , где , то число называют делителем числа , а число — кратным числа .

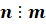
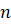
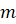
Вот такая запись означает, что делится на нацело.

Натуральное число, не равное единице, называется простым, если оно имеет только два делителя: единицу и само это число.

Например: 2, 3, 5, 7, 11, 17 — простые числа.

Натуральное число называется составным, если оно имеет более двух делителей. Например: 6, 15, 24, 36 — составные числа.

Число 1 не является ни простым, ни составным. Простых чисел бесконечно много. Каждое составное число разлагается на простые множители и притом единственным образом.

Сформулируем признаки делимости натуральных чисел:

1. Для делимости на 2 нужно, чтобы последняя цифра числа была чётная или .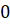

2. Для делимости на 3 нужно, чтобы сумма цифр числа делилась на 3.

3. Для делимости на 4 нужно, чтобы две последние цифры числа были или образовывали число, делящееся на 4.

4. Для делимости на 5 нужно, чтобы последняя цифра числа была 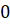или 5.

5. Для делимости на 8 нужно, чтобы три последние цифры числа были 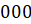или образовывали число, делящееся на 8.

6. Для делимости на 9 нужно, чтобы сумма цифр числа делилась на 9.

7. Для делимости на 10 нужно, чтобы последняя цифра числа была .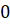

8. Для делимости на 11 нужно, чтобы разность между суммой цифр, стоящих на чётных местах, и суммой цифр, стоящих на нечётных местах, делилась на 11.

9. Для делимости на 25 нужно, чтобы две последние цифры числа были 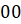или образовывали число (25, 50 или 75), делящееся на 25.

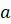
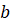
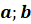
Наибольшее из натуральных чисел, на которое делятся числа и , называется их наибольшим общим делителем и обозначается НОД ().

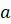
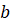
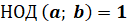
Числа и называются взаимно обратными, если .

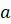
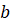
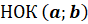
Наименьшее из натуральных чисел, которое делится на числа и , называется их наименьшим общим кратным и обозначается .

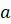
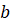
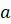
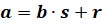
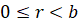
Разделить натуральное число на натуральное число с остатком – это значит представить в виде: , где .

Например, .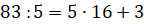

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задание первое. Найдите значение выражения .

Задание второе. Найдите наибольшее натуральное число, которое при делении на 15 с остатком даёт частное, равное 19.

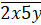
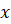
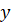
Задание третье. Найдите все натуральные числа вида (здесь — цифра сотен, — цифра единиц), которые делятся на 12. В ответ запишите их количество.

Задание четвёртое. Произведение двух чисел равно 10 800, а их НОД равен 60. Найдите НОК этих чисел.

Задание пятое. Найдите все пары натуральных чисел, НОД которых равен 5, а НОК равно 105.

Задание шестое. Сумма цифр искомого двузначного числа равна 8. Если цифры этого числа переставить, то получится число, которое меньше искомого на 18. Как велико искомое число?

Задание седьмое. В двузначном числе цифра десятков на 4 больше цифры единиц. Когда это число разделили на цифру единиц, то в частном получилось 24, а в остатке число, которое на 2 меньше делителя. Найдите заданное число.

Задание восьмое. В комнате стоят табуретки и стулья. У каждой табуретки по 3 ноги, у каждого стула по 4 ноги. Когда на всех табуретках и стульях сидят люди, то в комнате всего 39 ног. Сколько стульев и сколько табуреток в комнате?

Задание девятое. Когда брату было столько лет, сколько сестре сейчас, им вместе было 15 лет; когда сестре будет столько лет, сколько сейчас брату, им вместе будет 27 лет. Найдите возрасты брата и сестры.

Источник

«Интересные свойства чисел»

Слет научных обществ обучающихся

образовательных организаций общего и дополнительного образования

города Нижневартовска в 2017-2018 учебном году

Секция 5. «Прикладная математика »

Интересные свойства чисел

Дадажанова Карина Руслановна,

муниципальное бюджетное общеобразовательное

учреждение «Средняя школа № 1»,

Якоби Зинаида Фёдоровна,

муниципальное бюджетное общеобразовательное

учреждение «Средняя школа 1»

Интересные свойства чисел

Дадажанова Карина Руслановна

Муниципальное бюджетное общеобразовательное учреждение

Цель: Однажды мне попалась на глаза книга «Удивительный мир чисел». Ее авторы В. А. Кордемский, А.А. Ахадов отдают предпочтение стихии чисел, раскрывают внутреннюю красоту их разнообразных свойств. Изучая специальную литературу, произведя несложные расчеты и сравнения, воспользовавшись ресурсами Интернет я постаралась как можно больше узнать о числах, о науке, которая их изучает, об ученых математиках древности и современности, которые занимались изучением теории чисел.

Практически все математические понятия, так или иначе, опираются на понятие числа, а конечный результат любой математической теории, как правило, выражается на языке чисел. Многие из них, особенно натуральные числа по тем или иным признакам и свойствам сгруппированы в отдельные структуры (совокупности) и имеют собственные имена.

Я поставила перед собой цель найти такие числа, которые объединены между собой интересными закономерностями или наоборот, не подчиняются каким-либо правилам.

Объект исследования – числа

1. Изучение доступной литературы по данной теме

2. Изучить свойства чисел

3. Произвести проверку

Интересные свойства чисел

Дадажанова Карина Руслановна

Муниципальное бюджетное общеобразовательное учреждение

1.Мы каждый день в повседневной жизни сталкиваемся с числами. Чтобы пользоваться числами, нужно знать их свойства. Поэтому я выбрала данную тему.

2. Я поставила перед собой цель найти такие числа, которые объединены между собой интересными закономерностями или наоборот, не подчиняются каким-либо правилам.

Объектная область : математика

Выбор темы: Математические закономерности чисел

Гипотеза :у знать свойства чисел, которые в школьном курсе математики не рассматриваются, произвести вычисления и доказать, что эти числа действительно подчинятся заданным критериям.

1. Изучение доступной литературы по данной теме

2. Изучить свойства чисел

3. Произвести проверку

Методы исследования: теоретический, анкетирование, анализ.

Сбор и изучение материала по теме исследования:

2. Корнеев А.А. «Познание чисел – «вмещением». Глобальный принцип Улама & Ко (гипотеза)» М., 2007-2008.

3. Пичурин Л. Ф. За страницами учебника алгебры: книга для учащихся 7-9 классов – М.: «Просвещение», 2007 – 224 с.

4. Школьная энциклопедия «Математика. Том 11». Издательство «Аванта+»., М. 2007.

5. «Энциклопедический словарь юного математика» Сост. Савин А.П. – М.: Педагогика, 2005.

6. Я познаю мир. Математика: энцикл. /авт. – сост. А. П. Савин, В. В. Станцо, А. Ю. Котова. – М.: АСТ:Астрель:Люкс, 2005– 475 с.

Моделирование средствами программы Microsoft PowerPoint математической закономерности чисел, позволяющей натуральные числа по тем или иным признакам и свойствам сгруппировать в отдельные структуры

Презентация результатов исследования.

Анализ результатов опроса обучающихся моего класса.

Оформление исследовательского проекта

Интересные свойства чисел

Дадажанова Карина Руслановна

Муниципальное бюджетное общеобразовательное учреждение

Научная статья (описание работы)

Одна за всех и все за одного

Интересное число 50

Интересные свойства числа 9

Предмет математики столь серьёзен,

что не следует упускать ни одной возможности

сделать его более занимательным

Всё мы со школьной скамьи изучаем математику: цифры, числа, выражения… Мы привыкли решать всё по заданным алгоритмам, по правилам, и ни когда не задумывались о свойствах чисел. Ведь в любой закономерности есть исключение, в любом законе найдётся лазейка и про каждое число можно рассказать что-то интересное. Каждое число чем-то отличается от других, а чем-то и похоже.

Мы каждый день в повседневной жизни сталкиваемся с числами. Чтобы пользоваться числами, нужно знать их свойства. Поэтому я выбрала данную тему.

Узнать свойства чисел, которые в школьном курсе математики не рассматриваются, произвести вычисления и доказать, что эти числа действительно подчинятся заданным критериям.

Цель исследования: Я поставила перед собой цель найти такие числа, которые объединены между собой интересными закономерностями или наоборот, не подчиняются каким-либо правилам.

1. Изучение доступной литературы по данной теме

2. Изучить свойства чисел

3. Произвести проверку

Объект исследования – числа.

Методы исследования: теоретический, анкетирование, анализ.

Научная статья (описание работы)

Возьмём любое натуральное число, например, 12. Переставим в нём цифры в обратном порядке и сложим с исходным числом.

Мы получили число-палиндром, одинаково читающееся как справа налево, так и слева направо. Иногда, чтобы получить палиндром, требуется больше шагов. Вот, например, для числа 192:

Сделано 4 шага и палиндром, 6996, получен.

13783 + 38731 = 52514

52514 + 41525 = 94039

94039 + 93049 = 187088

187088 + 880781 = 1067869

Само число уже превышает миллион, а палиндром не получен! И до сих пор не найдено ни на каком шагу из числа 196 получится палиндром (а таких шагов разными исследователями с помощью компьютера сделано более семисот миллионов), ни строгого доказательства, что палиндром не будет получен никогда. Числа, которые, как и 196, не дают палиндром после некоторого числа шагов, называются числами Лишрел.

Одна за всех и все за одного

Интересное число 50

Если заменить слово «натуральных» словом «целых», то наименьшим числом такого рода будет 25: 25 = 16 + 9 = 0 + 25.

Разложим натуральное число на простые множители. Запись его разложения может иметь как больше цифр, чем само число (например, 2013 = 3*11*61), столько же цифр (27=3 3 ) или даже быть короче (1701 = 37*7)

Поскольку здесь мы имеем дело с цифрами, то в разных системах счисления разные числа окажутся репдигитами. Например, число 26 будет репдигитом в троичной системе, ведь там оно выглядит как 222.

Числа 153, 370, 371, 407

1741725; 4210818; 9800817; 9926315

*24678050; 24678051; 88593477

146511208; 472335975; 534494836; 912985153

32164049650; 32164049651; 40028394225; 42678290603; 44708635679; 49388550606; 82693916578; 94204591914

4937775 = 3 х 5 х 5 х 65837-разложение на простые множители

Интересные свойства числа 9

Часто применяются в арифметике как для теоретических изысканий и практических действий, так и для составления различных занимательных задач или так называемых «головоломок». Распространено также практическое применение девятки для проверки умножения и деления. Основано оно на том свойстве всякого числа, что остаток, получаемый от деления числа на девять, всегда равен остатку от деления на 9 суммы цифр этого числа. Укажем здесь еще несколько интересных применений этого числа. Прежде всего нетрудно убедиться, что если мы напишем произвольное двузначное число, а затем напишем цифры этого же числа в обратном порядке и возьмем разность полученных чисел, то эта разность всегда разделится на 9. Например, 72 − 27 = 45; 92 − 29 = 63; 63 − 36 = 27 и т. д. Вообще ясно, что (10a + b) − (10b + a) = 9(a − b), т. е. получается число, делящееся на 9. (Кроме того разность эта равна произведению 9 на разность цифр данного двузначного числа.) Знание этой особенности может принести практическую пользу, например, многим бухгалтерам.

Написав эту работу, я узнала о многих и интересных задачах, связанных со свойствами натуральных чисел, об истории этих задач. Познакомилась с русскими и зарубежными учеными математиками, внесшими большой вклад в теорию чисел.

Для написания этой работы мне пришлось прочитать много книг. Книги эти особенные, математические. В них рассматривается то, что мы вроде бы изучаем на уроках математики, но с какой – то другой стороны. Оказывается такая сухая и скучная наука, как математика, может быть интересной и занимательной.

Читать математические книги пришлось не просто так, а с карандашом в руках, решая предложенные задачи, производя несложные практические расчеты. Легких математических книг не бывает.

Написав эту работу, я хочу дать всем совет. Математику нужно изучать самостоятельно, но очень полезно обсуждать прочитанное и изученное в небольшом коллективе.

Математика – предмет непростой. Людей совершенно неспособных к математике не бывает. Испытать себя в математике можно очень рано. Не случайно многие открытия были сделаны людьми, не достигшими тридцати, а иногда и 20 лет.

В своей работе я постаралась узнать свойства чисел, которые в школьном курсе математики не рассматриваются, произвела вычисления и доказала, что эти числа действительно подчинятся заданным критериям.

8. Корнеев А.А. «Познание чисел – «вмещением». Глобальный принцип Улама & Ко (гипотеза)» М., 2007-2008.

9. Пичурин Л. Ф. За страницами учебника алгебры: книга для учащихся 7-9 классов – М.: «Просвещение», 2007 – 224 с.

10. Школьная энциклопедия «Математика. Том 11». Издательство «Аванта+»., М. 2007.

11. «Энциклопедический словарь юного математика» Сост. Савин А.П. – М.: Педагогика, 2005.

12. Я познаю мир. Математика: энцикл. /авт. – сост. А. П. Савин, В. В. Станцо, А. Ю. Котова. – М.: АСТ:Астрель:Люкс, 2005– 475 с.

· 0 (нуль) Величайшее изобретение человеческого разума, давшего исходный импульс развитию математике как таковой. Согласитесь – невероятно трудно придумать «ничего», дать ему имя и использовать в вычислениях. Самые интересные свойства – на нуль нельзя делить, нуль, будучи показателем степени, приравнивает любое число к единице. Умножение на нуль дает нуль. Сложение и вычитание его результат не меняет. Использование нуля позволяет создавать позиционные системы счисления (в отличие, например, от римских цифр, обходившихся без нуля). О следующих числах предельно кратко.

· 1 Дает тождество при умножении. Равно любому числу в нулевой степени.

· 2 Единственное четное простое число.

· 3 Число размерностей пространства, в которых мы живем. Единственное число, равное сумме всех меньших чисел – естественно, речь все время идет о целых числах. Имеет горизонтальную ось симметрии.

· 4 Наименьшее число цветов для раскраски карты на плоскости. Тетраэдальное число.

· 5 Число Платоновых многогранников. Пятое число из последовательности Фибоначчи. Пирамидальное число.

· 6 =3! Наименьшее совершенное число. Треугольное число.

· 7 Наименьшее число сторон многоугольника, которым нельзя замостить плоскость. Шестиугольное число.

· 8 Наибольший куб в последовательности Фибоначчи. Имеет горизонтальную и вертикальную оси симметрии.

· 9 Максимальное число кубов, необходимое для представления в виде их суммы любого положительного целого числа.

· 10 Основание нашей системы счисления. Число топологически различных фигур из 5 спичек. Тетраэдальное и треугольное число.

· 11Наибольшее количество кусков, на которые делят круг 4 прямые линии. Имеет горизонтальную ось симметрии.

· 12 Наименьшее число, имеющее 4 делителя. Количество плиток пентамино.

· 13 Число Архимедовых многогранников. Число из последовательности Фибоначчи. Перестановочное (с 31) простое число.

· 14 Четвертое число Каталана. Пирамидальное число.

· 15 Четвертое число последовательности Белла. Треугольное число. Произведение первых трех нечетных чисел. Количество сочетаний четырех чисел из шести.

· 17 Количество вариантов узоров, построенных с использованием сдвигов, поворотов и отражений. Перестановочное (с 71) простое число.

· 18 Единственное число, равное удвоенной сумме его цифр.

· 19 Максимальное число четвертых степеней чисел, с помощью суммы которых можно выразить любое число. Шестиугольное число.

· 20 Число топологически различных фигур из 6 спичек. Тетраэдальное число. Количество сочетаний трех чисел из шести.

· 21 Число из последовательности Фибоначчи. Треугольное число. Количество сочетаний двух или четырех чисел из шести.

· 22 Количество кусков, на которые делят круг 6 прямых линий.

· 23 Количество деревьев с восемью звеньями.

· 24 =4! Самое большое число, которое делится на все числа, меньшие корня из него.

· 25 Наименьшее число, которое можно представить как сумму двух квадратов.

· 26 Наименьшее число не-палиндром, квадратом которого является палиндром.

· 27 Единственное (возможно?) число, у которого сумма цифр (9) суммы кубов цифр (8+343=351) с суммой цифр (18) куба суммы цифр (729) равна самому числу.

· 28 Второе совершенное и одновременно треугольное число.

· 29 Седьмое число Люка. Наибольшее количество кусков, на которые делят круг 7 прямых линий.

· 30 Самое большое число, у которого все числа меньшие его и взаимно простые с ним простые. Пирамидальное число.

· 31 Простое число Мерсенна. Перестановочное (с 13) простое число.

· 32 Наименьшая 5-ая степень числа (исключая 1)

· 33 Самое большое число, не равное сумме разных треугольных чисел. Имеет горизонтальную ось симметрии.

· 34 Наименьшее число такое, что имеет равное количество делителей с ближайшими соседними числами. Число из последовательности Фибоначчи

· 35 Количество плиток гексамино. Тетраэдальное число. Количество сочетаний трех или четырех чисел из семи.

· 36 Наименьшее число (кроме 1), которое одновременно и квадратное и треугольное.

· 37 Максимальное количество 5х степеней чисел, необходимое для выражения их суммой любого числа. Количество кусков, на которые делят круг 8 прямых линий. Шестиугольное число. Перестановочное (с 73) простое число.

· 38 Наибольшее римское число (по длине) в лексикографической записи (XXXVIII).

· 39 Три делителя этого числа пишутся одними и теми же цифрами.

· 40 Максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в пятимерном пространстве. Количество расстановок 7 ферзей на доске 7*7 не угрожающих друг другу.

· 42 Пятое число Каталана. Количество вариантов плоскостей гексагексафлексагона.

· 43 Количество гептиамондов. (Фигуры из 7 правильных треугольников)

· 44 Количество вариантов перемешивания пяти предметов.

· 45 число Капрекара. Треугольное число. Количество сочетаний двух или восьми чисел из десяти.

· 46 Количество участков, на которые делят круг 9 прямых линий.

· 47 Наибольшее число кубов, из которых нельзя сложить куб. Количество деревьев с девятью звеньями.

· 48 Наименьшее число, имеющее 10 делителей.

· 49 Наименьшее число такое, что оно само и его ближайшие соседи имеют среди делителей квадраты.

· 50 Наименьшее число, которое можно представить как сумму квадратов двумя способами. Число вариантов складывания полоски из 5 марок.

· 51 Шестое число Мотзкина.

· 52 Это пятое число Белла.

· 53 Является одним из чисел n, которые служат делителем суммы n первых простых чисел.

· 54 Наименьшее число, которое может быть представлено суммой трех квадратов тремя способами.

· 55 Наибольшее треугольное число среди чисел Фибоначчи. Пирамидальное число.

· 56 Количество вариантов Латинских квадратов. Тетраэдальное число.

· 57 = 111 по основанию 7.

· 58 Половина, сумма цифр и сумма квадратов цифр – простые числа.

· 59 Наименьшее число, представляемое четвертыми степенями чисел в форме a4+b4-c4.

· 60 Наименьшее число, имеющее своими делителями все числа от 1 до 6.

· 61 Это шестое число Эйлера. Шестиугольное число.

· 62 Наименьшее число, которое может быть представлено суммой трех квадратов двумя способами.

· 63 Количество вариантов упорядочивания множества из 5 элементов.

· 64 Наименьшее число, имеющее 7 делителей.

· 65 Еще одно (как и 50) число, которое можно представить как сумму квадратов двумя способами.

· 66 Треугольное число. Количество сочетаний двух или десяти чисел из двенадцати.

· 67 Наименьшее число, которое будет палиндромным, если его представить по основанию 5 или 6.

· 68 Попытка проследить последовательные суммы квадратов цифр сразу обрывается, так как ряд замыкается.

· 69 интересно тем, что n2 и n3 вместе содержат все цифры.

· 70 Количество сочетаний четырех элементов из восьми.

· 71 Делитель суммы всех простых чисел, меньших его самого. Перестановочное (с 17) простое число.

· 72 Максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в шестимерном пространстве.

· 73 Наименьшее из чисел (исключая 1), которое меньше удвоенного числа с перевернутыми цифрами (37*2=74). Перестановочное (с 37) простое число.

· 74 Одно из чисел с таким свойством, что сумма его с перевернутым числом равна квадрату суммы его цифр (74+47=11^2). Число областей, на которые делят плоскость 9 пересекающихся окружностей.

· 75 Если сложить сумму цифр с их произведением и повторять эту операцию, то вскоре зациклимся на числе 39.

· 76 Количество треугольников, которые можно сложить из зубочисток 6 цветов.

· 77 Наибольшее число, которое не может быть представлено суммой ряда чисел, начиная с 1.

· 78 Наименьшее число, которое может быть представлено суммой четырех квадратов тремя вариантами. Треугольное число. Количество сочетаний двух или одиннадцати чисел из тринадцати.

· 79 Перестановочное простое число, так как 97 тоже простое.

· 80 Наименьшее число n такое, что n и n+1 оба являются произведениями четырех и более простых чисел.

· 81 Квадрат суммы цифр.

· 82 Пятиугольное число.

· 83 Еще одно из чисел с таким свойством, что сумма его с перевернутым числом равна квадрату суммы его цифр.

· 84 Тетраэдальное число. Количество сочетаний трех или шести чисел из девяти. Количество областей, на которые делят пространство 7 сфер.000

· 85 Если взять сумму квадратов цифр и повторять эту операцию, то вскоре попадем в замкнутое кольцо, в котором, что самое интересное, число 85 не участвует.

· 86 = 222 по основанию 6.

· 88 Единственное число из двух одинаковых цифр, квадрат которого содержит две пары одинаковых цифр. Имеет горизонтальную и вертикальную оси симметрии.

· 89 = 81 + 92 Число из последовательности Фибоначчи.

· 90 Число десятков равно количеству делителей (не считая 1)

· 91 Запишется как 10101 по основанию 3. Шестиугольное число. Самое большое число, для которого выполняется равенство 12+22+32+. +n2 = 1+2+3+. +m, поэтому оно пирамидальное и еще и треугольное число.

· 92 Число расстановок восьми ферзей на шахматной доске так, чтобы они не угрожали друг другу. Число областей, на которые делят плоскость 10 пересекающихся окружностей.

· 93 = 333 по основанию 5.

· 94 Половина, сумма цифр и сумма квадратов цифр – простые числа.

· 95 Количество вариантов разделения плоскости на 10 областей.

· 96 Наименьшее число, которое можно представить как сумму квадратов четырьмя способами.

· 97 Наименьшее из чисел, три первых кратных которого содержат цифру 9. Перестановочное (с 79) простое число.

· 98 Наименьшее из чисел, пять первых кратных, которого содержат цифру 9.

· 99 Число Капрекара, так как 992=9801, а 98+01=99.

· 100 Наименьший квадрат, равный сумме кубов четырех последовательных чисел.

Источник