Общая сторона угла что это

Математика

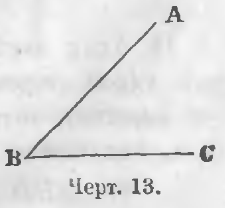
Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.

Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.

Стороны угла. Пересекающиеся линии называются сторонами угла.

Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.

Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.

На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.

Таким образом угол ABC есть угол B или

Знак угла. Слово угол заменяют иногда знаком ∠.

Таким образом предыдущее равенство изображают письменно:

В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.

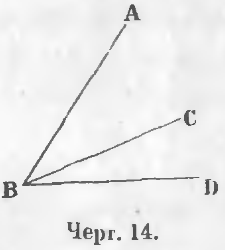
На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.

Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.

Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.

Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14

уг. ABD > уг. ABC и уг. CBD уг. DEF.

c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF

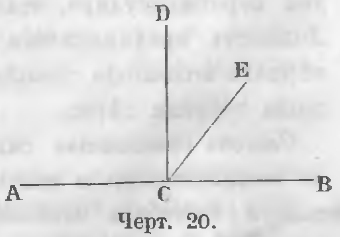
На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.

Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.

Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.

Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.

Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.

Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.

Дана прямая AB и на ней точка C (черт. 20).

Требуется доказать, что можно к ней восставить только один перпендикуляр.

Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра

уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.

Если приложить к первой части последнего неравенства угол ECD, получим неравенство

уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.

Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим

неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.

Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.

Теорема 4. Все прямые углы равны.

Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.

Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.

Заключение. Прямой угол есть величина постоянная.

Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.

В таком случае
всякий острый угол d.

Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.

Теорема 5. Сумма двух смежных углов равна двум прямым.

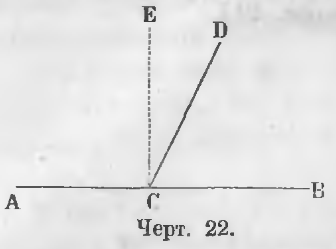
Даны смежные углы ACD и DCB (черт. 22).

Требуется доказать, что ACD + DCB = 2d.

Доказательство. Из точки C восставим перпендикуляр CE, тогда

Сложив эти равенства, имеем:

ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).

Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.

Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.

Теорема 6 (обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.

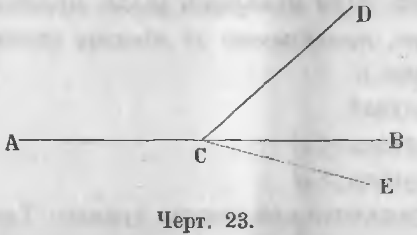
Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).

Требуется доказать, что ACB прямая линия.

Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда

Две величины равные одной и той же третьей равны (аксиома 3), следовательно

ACD + DCB = ACD + DCE

откуда выходит при сокращении

заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).

Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.

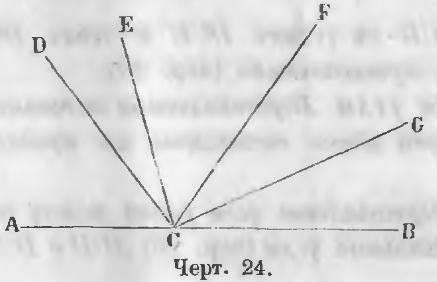
Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).

Требуется доказать, что

ACD + DCE + ECF + FCG + GCB = 2d.

Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).

Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:

ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).

Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.

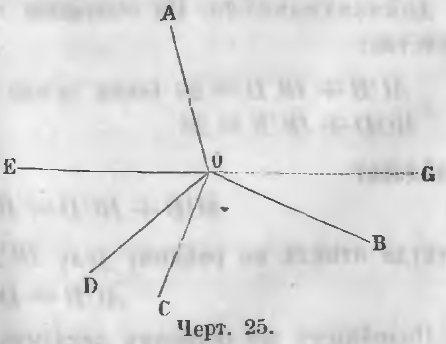
Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).

Требуется доказать, что

AOB + BOC + COD + DOE + EOA = 4d.

Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда

GOB + BOC + COD + DOE = 2d.

Сложив эти равенства, имеем:

EOA + AOG + GOB + BOC + COD + DOE = 4d.

Так как AOG + GOB = AOB, то

EOA + AOB + BOC + COD + DOE = 4d (ЧТД).

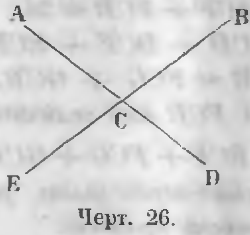
Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).

Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.

Теорема 9. Вертикальные углы равны между собой.

Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.

Требуется доказать, что ACB = DCE и BCD = ACE.

Доказательство. На основании теоремы 5 имеют место равенства:

ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d

ACB + BCD = BCD + DCE

откуда, отняв по равному углу BCD, находим

Подобным же образом доказывают, что

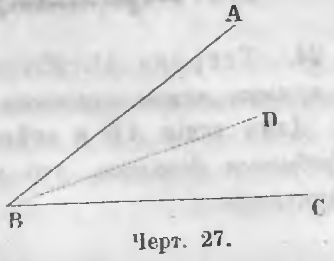
Равносекущая (биссектриса) есть линия, делящая угол пополам.

На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.

Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.

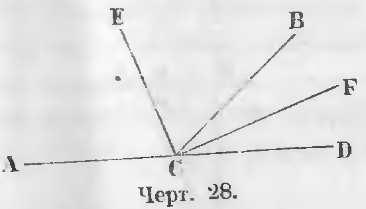
Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.

Требуется доказать, что EC ⊥ CF.

Доказательство. По условию

ECB = ½ ACB, BCF = ½ BCD

Сложив эти равенства, имеем:

ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).

Так как ACB + BCD = 2d, то

Так как ECB + BCF = ECF, то

Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).

Источник

Общая сторона угла что это

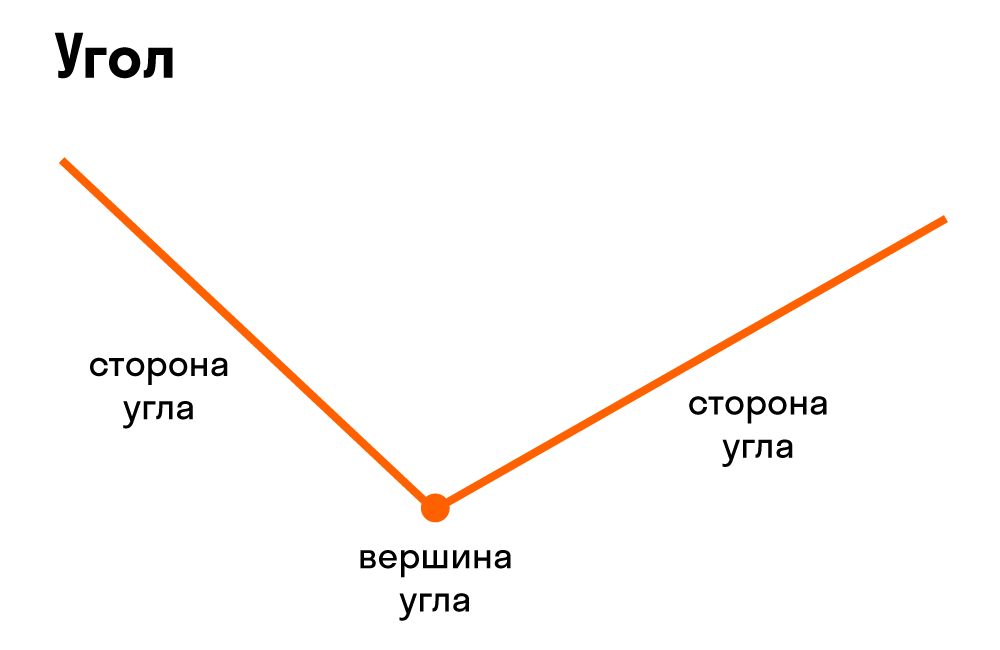
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.

Лучи называются сторонами угла, а их общее начало − вершиной угла.

Обозначение угла

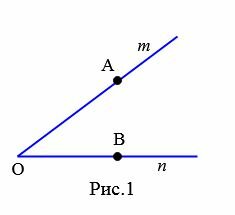
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)

Развернутый угол. Внутренняя и внешняя область угла

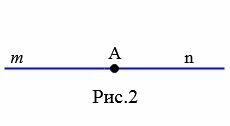
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.

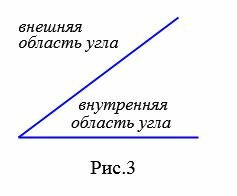
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).

Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.

Фигуру, состоящую из угла и его внутренней области также называют углом.

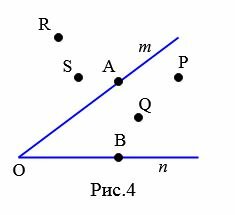
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.

Типы углов

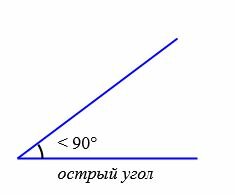
В зависимости от величин, углы бывают следующих типов (Рис.5):

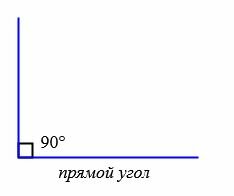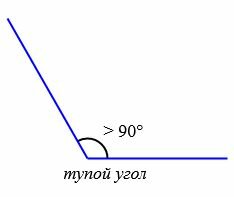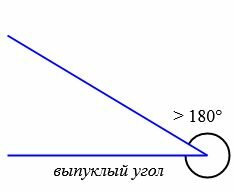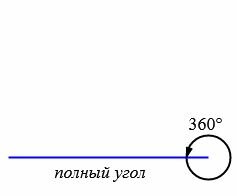Сравнение углов

Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.

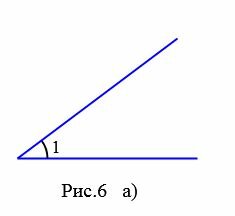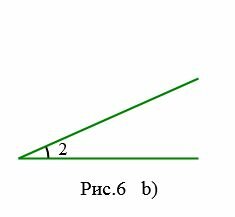На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)

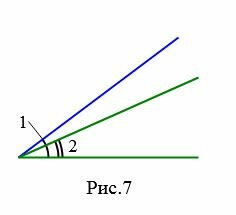Градусная мера угла

Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).

Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)

Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.

Источник

Угол. Основные понятия.

Когда два луча (AO и OB) исходят из одной точки, то фигура, сформированная этими лучами (вместе с частью плоскости, ограниченной ими), называется углом.

Стороны угла следует представлять себе бесконечно продолженными от вершины.

Угол обыкновенно обозначается тремя буквами, из которых средняя ставится у вершины, а крайние у каких-нибудь точек сторон. Например, говорят “угол АОВ или угол ВОА”. Но можно обозначать угол и одной буквой, поставленной у вершины, если при этой вершине других углов нет. Мы иногда будем обозначать угол цифрой, поставленной внутри угла у вершины. Слово “угол” на письме часто заменяется знаком /.

Когда два луча исходят из одной точки, то строго говорят, что они образуют не один угол, а два угла.

Эти два угла равны друг другу лишь в том случае, когда лучи AO и OB составляют одну прямую.

Такой угол называют развернутым углом.

Два угла считаются равными углами, если при наложении они могут совместиться.

Мы принимаем как очевидное, что внутри всякого угла из его вершины можно провести луч (и притом только один), который делит этот угол пополам. Такой луч называется биссектрисой угла.

Два угла (AOB и BOС) называются смежными, если одна сторона у них общая, а две другие стороны составляют прямую линию.

Когда два смежных угла равны (черт. 2), то общая сторона их OB называется перпендикуляром к прямой AC, на которой лежат другие стороны.

Если же смежные углы неравны (черт. 1), то общая сторона OB называется наклонной к AC.

В том и в другом случае точка O называется основанием (перпендикуляра или наклонной).

Из всякой точки прямой можно, по ту и другую сторону от этой прямой, восставить к ней перпендикуляр и притом только один.

Всякий развернутый углом равен 2 d = 180°.

Всякий угол (АОС), меньший прямого угла (АОВ) называется острым.

Всякий угол (AOD) больший прямого называется тупым.

Источник

Что такое угол? Виды углов

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

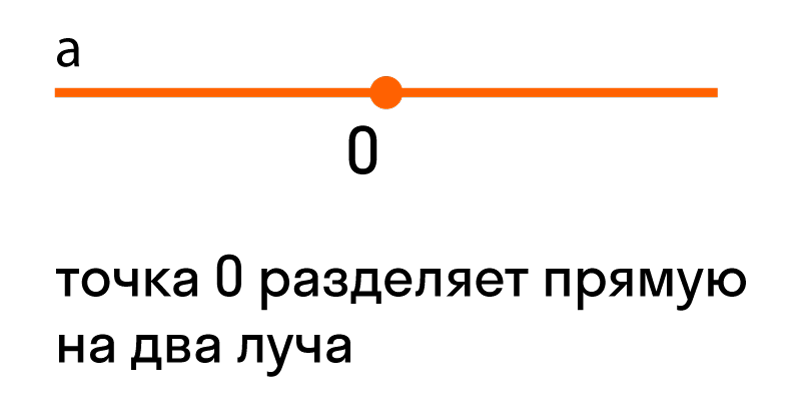
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

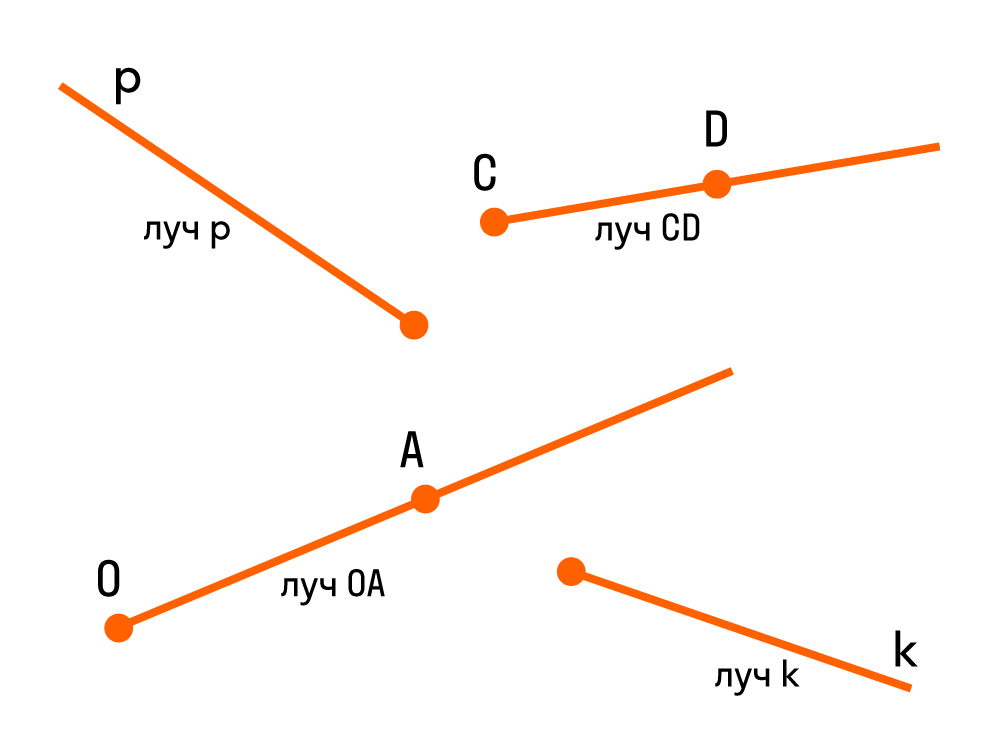
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

Что такое вершина и стороны угла

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

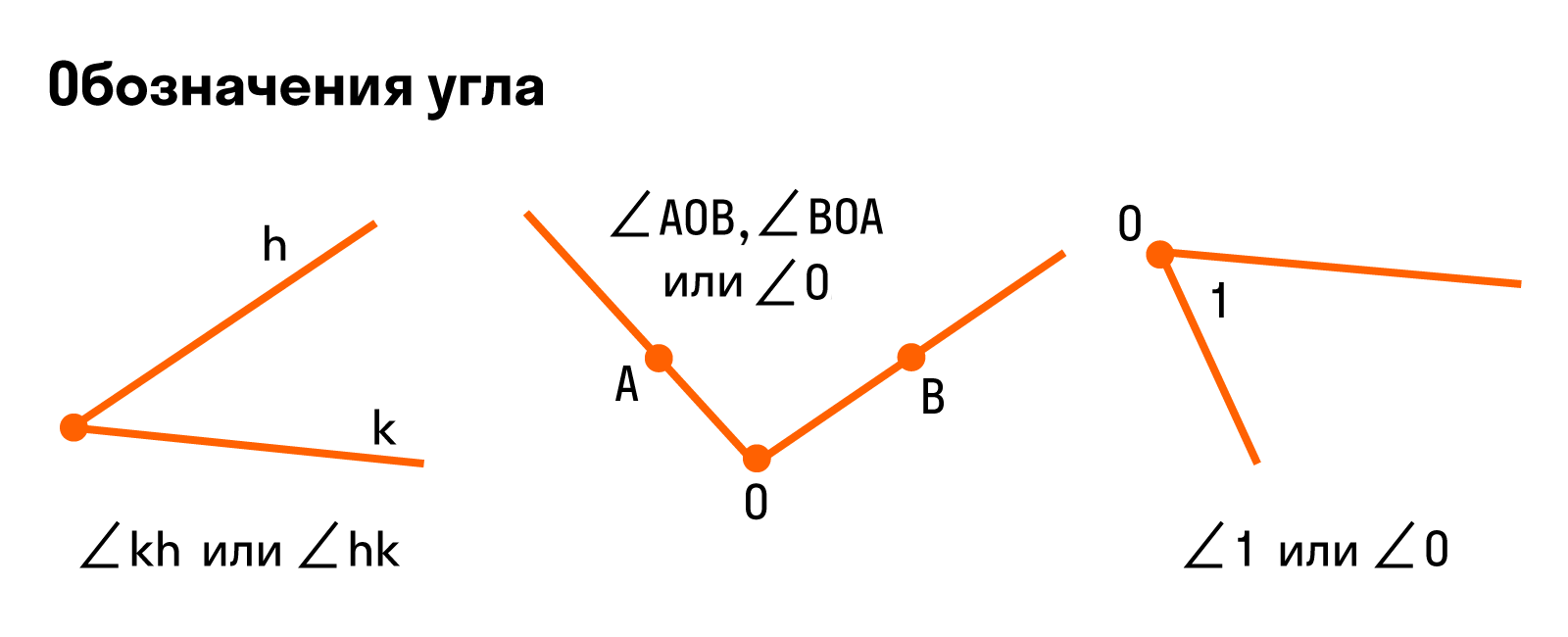
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.

Иногда встречается обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

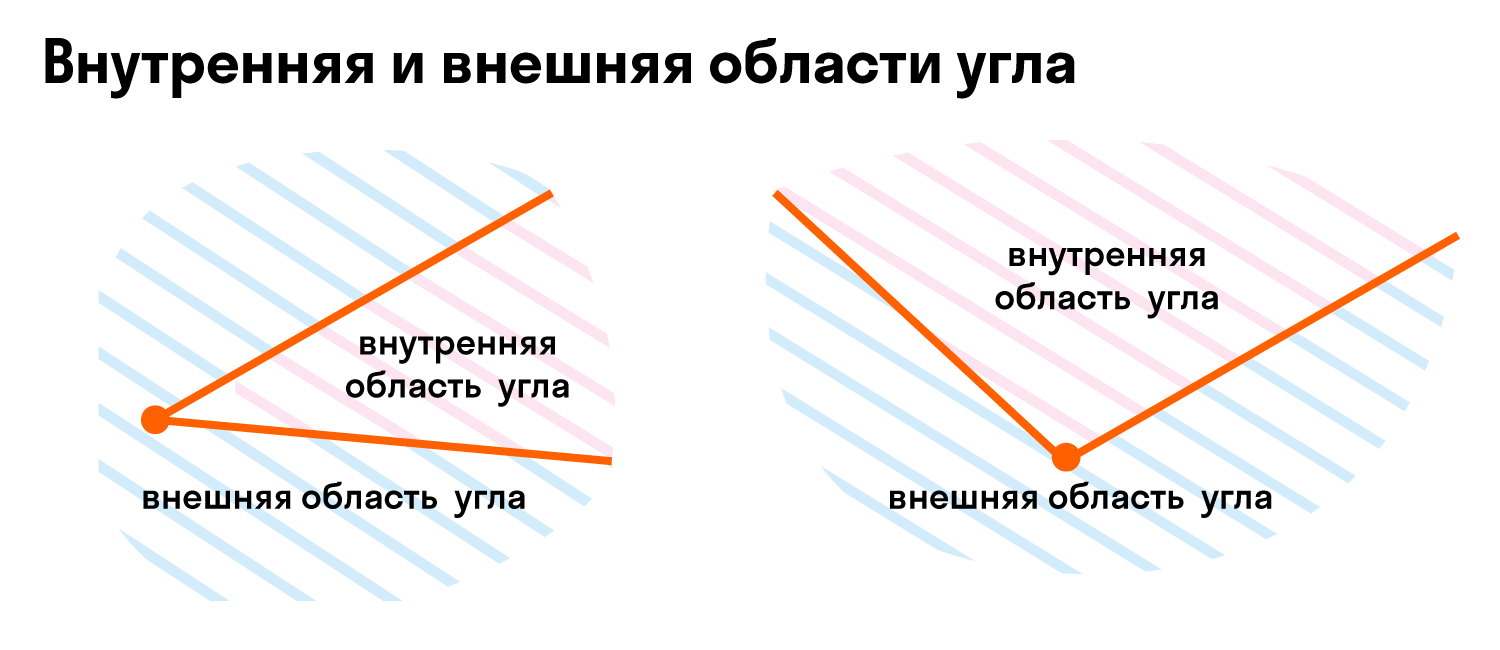
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Виды углов

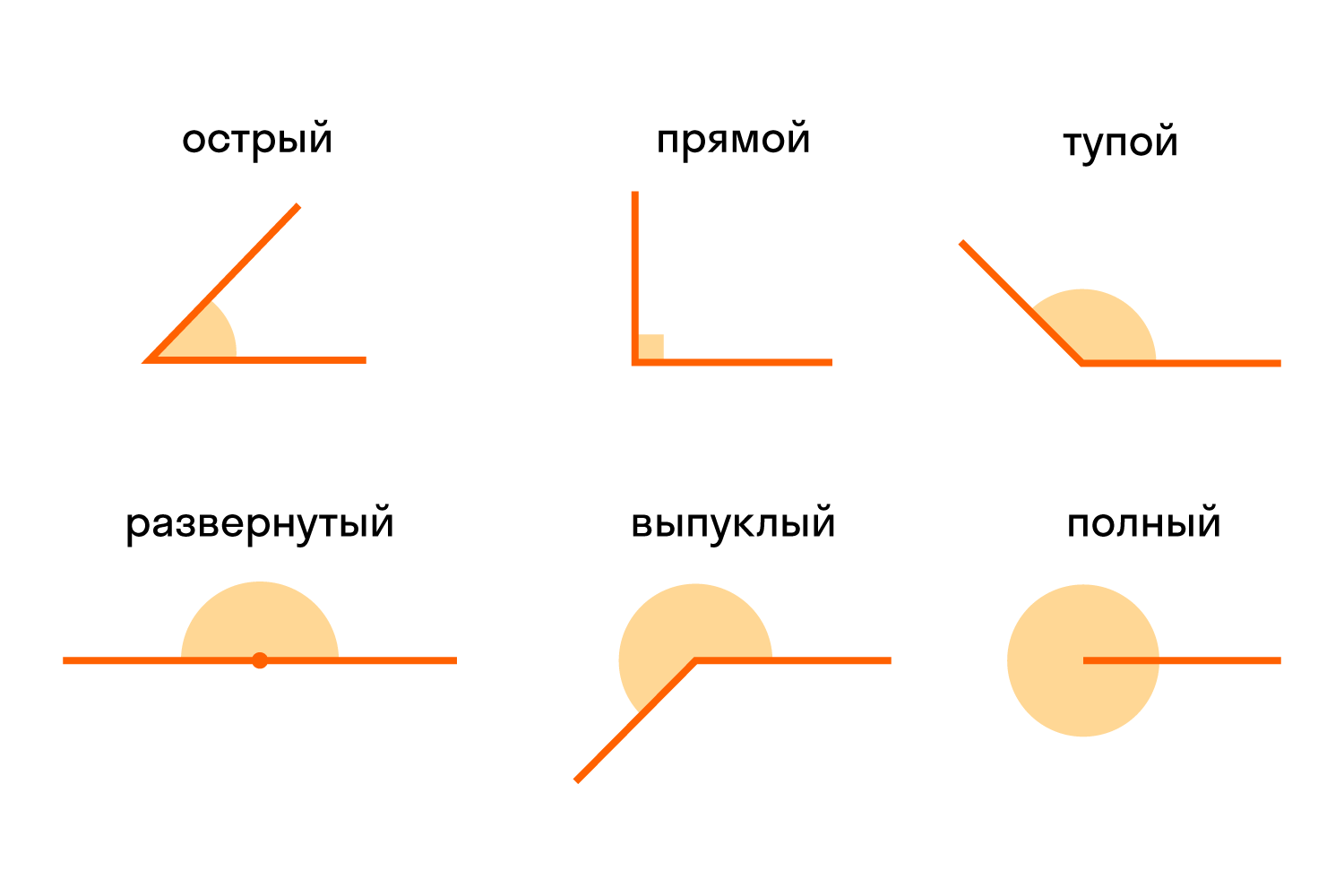
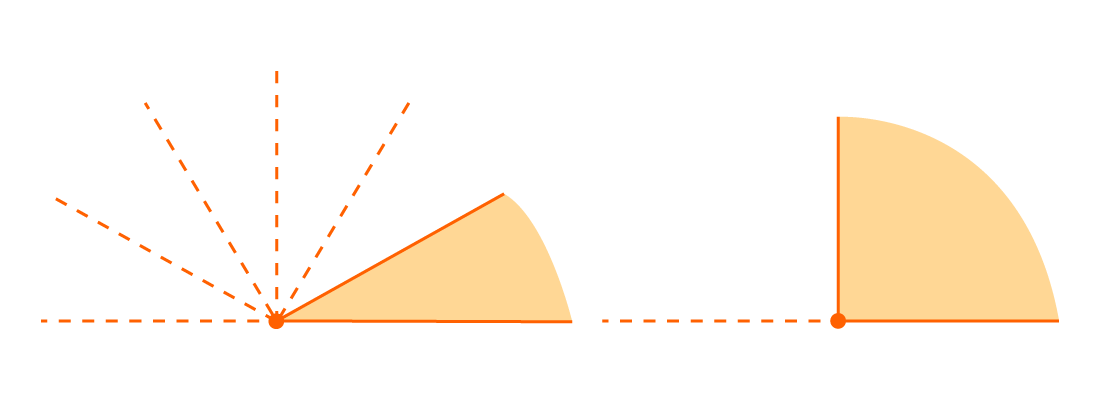
Есть разные типы углов и у каждого своё название:

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

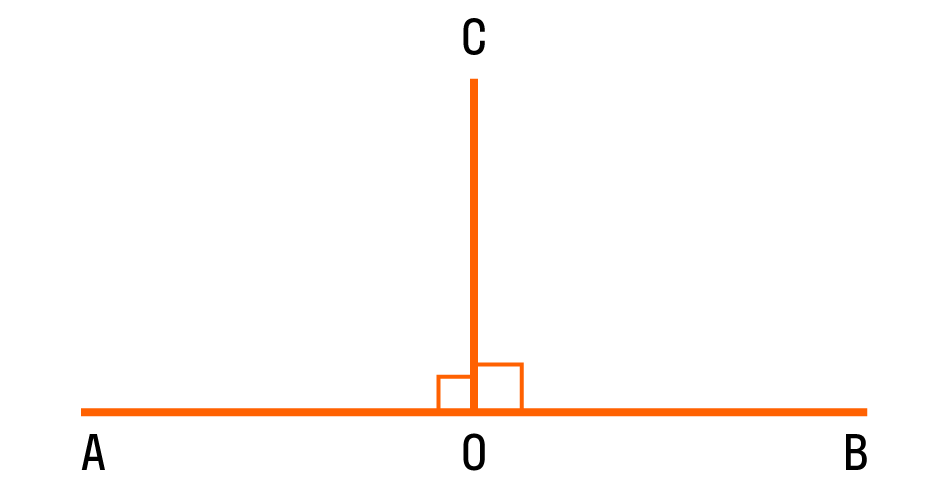
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Сравнение углов

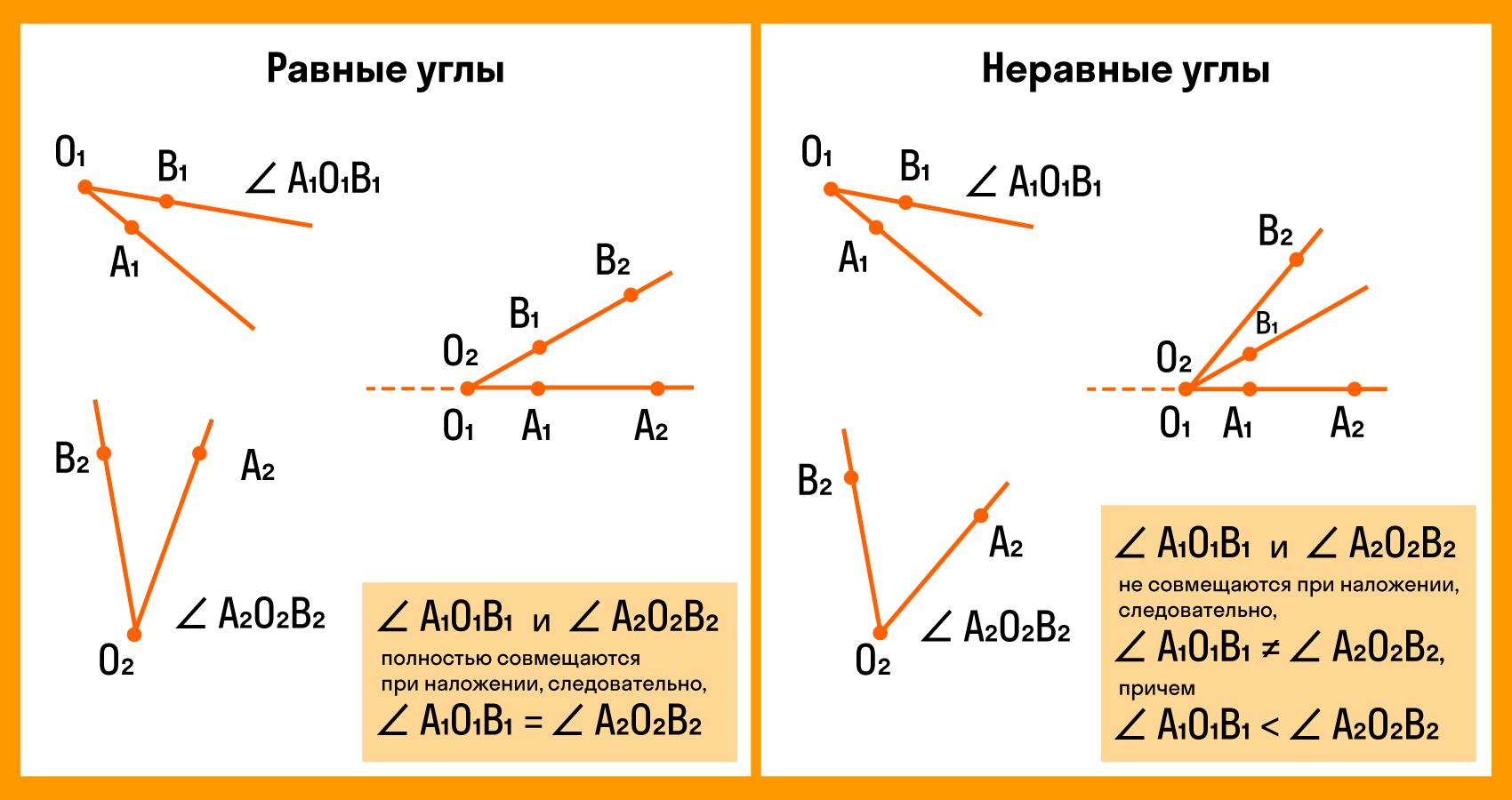
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

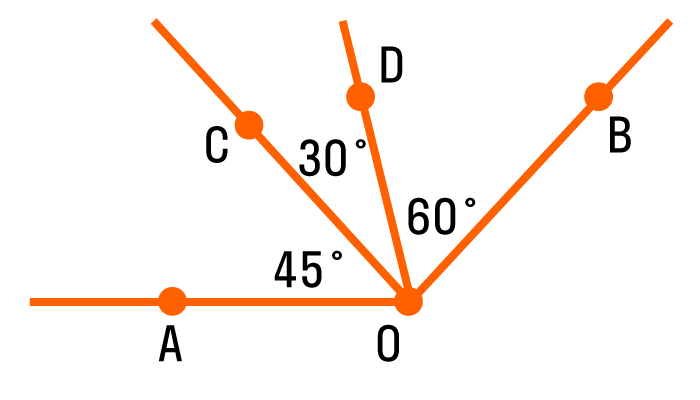
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

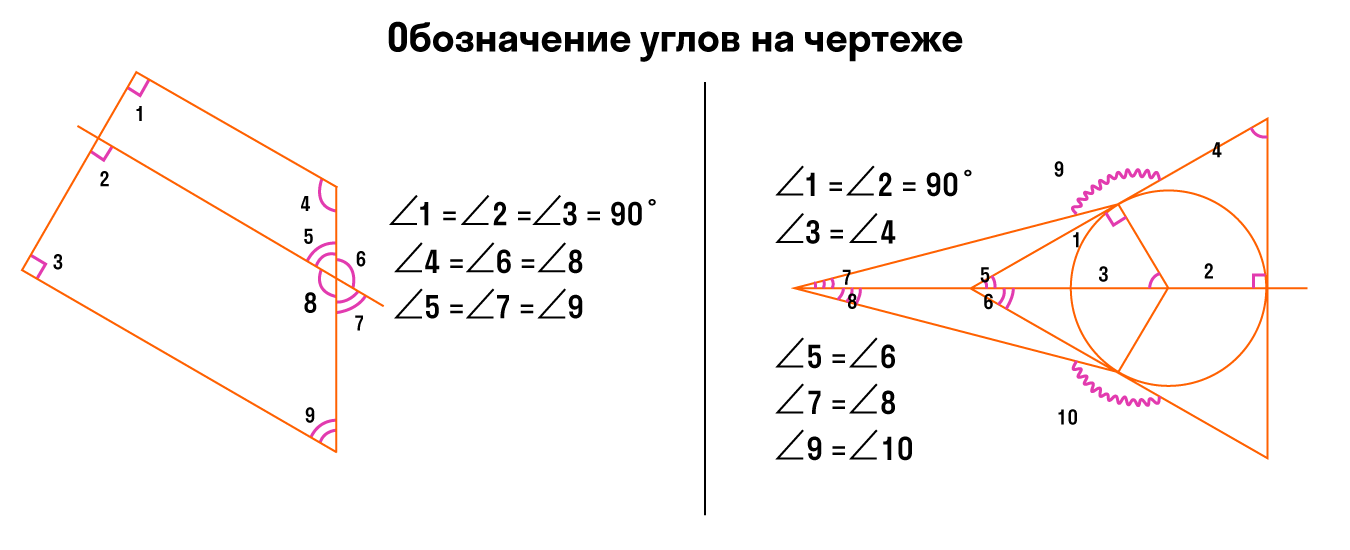
Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:

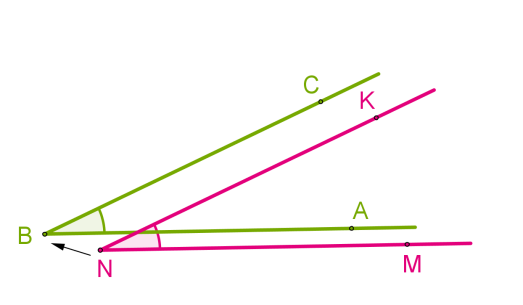
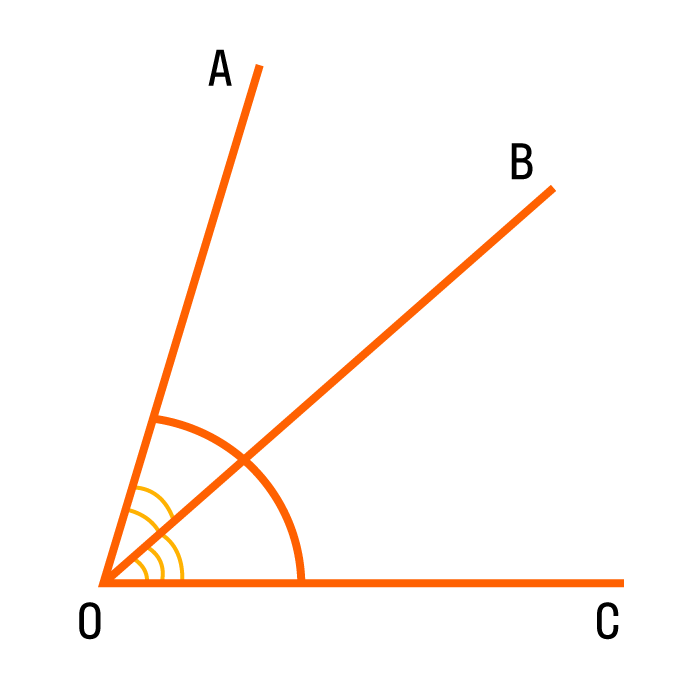
На чертеже отмечены три неравных угла:

Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Источник

Общая сторона угла что это

Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, то есть два луча с общим началом называются углом. Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.

Обозначение углов

Угол обозначается или одной буквой или цифрой, поставленной при вершине угла, например угол A или угол 1, или тремя буквами, из которых одна стоит при его вершине, а две другие при каких-либо точках его сторон. При обозначении угла тремя буквами, буква, стоящая при его вершине, произносится и пишется между двумя другими, например угол AOB. Слово угол в записи заменяют знаком ∠, например ∠1.

Внутренняя и внешняя область

Два луча, исходящие из одной точки, образуют два угла. Для обозначения нужного угла, угол обычно помечается дугой:

Если рассматриваются оба угла, образованные двумя лучами, то они помечаются разным числом дуг, но только в том случае, если углы не равны. Равные углы обозначаются одинаково.

Любой угол делит плоскость на две области. Одна область обычно называется внутренней, а другая внешней. Внутренняя область угла — это часть плоскости, расположенная между сторонами рассматриваемого угла:

Внешняя область угла — это часть плоскости, которая не принадлежит рассматриваемому углу.

Источник