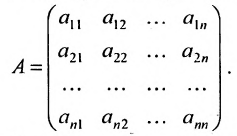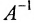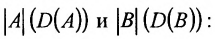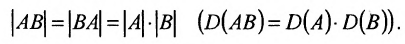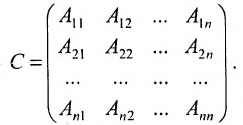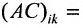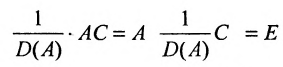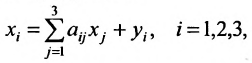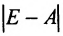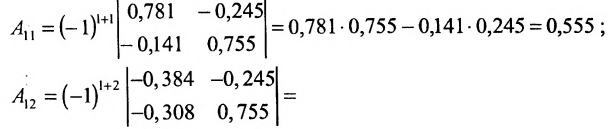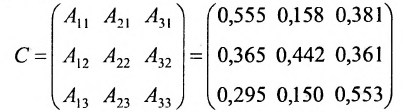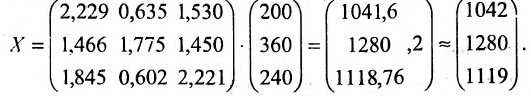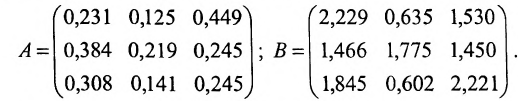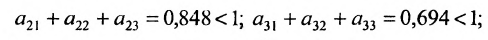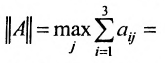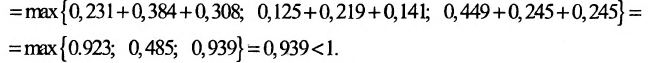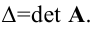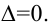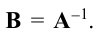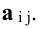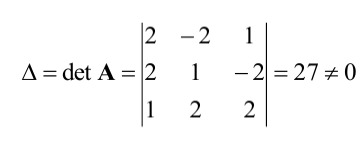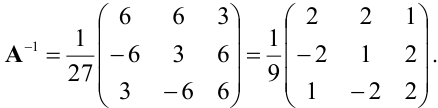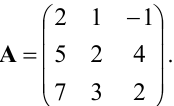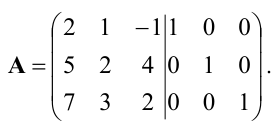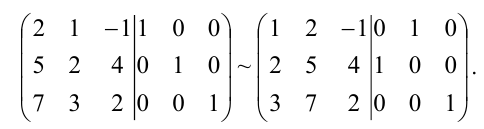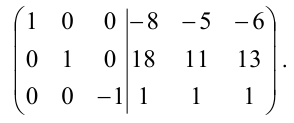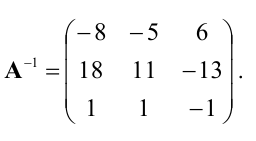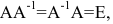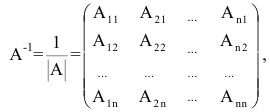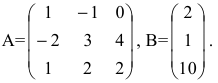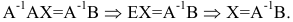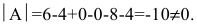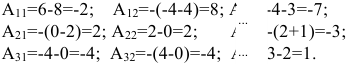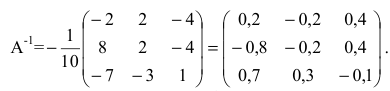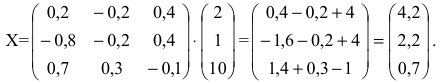Обратной к матрице a называется матрица a 1 такая что
Обратная матрица.
Метод обратной матрицы.
Метод обратной матрицы – это один из самых распространенных методов решения матриц и применяется для решения систем линейных алгебраических уравнений (СЛАУ) в случаях, когда число неизвестных соответствует количеству уравнений.
Суть метода обратной матрицы.
Пусть есть система n линейных уравнений с n неизвестными:
Такую систему можно записать как матричное уравнение A* X = B,
где 
– матрица системы,
– столбец неизвестных,
– столбец свободных коэффициентов.
Обратная матрица к матрице A существует лишь тогда, когда det A ≠ 0. Ввиду этого при решении СЛАУ методом обратной матрицы первым делом находится det A. Если det A ≠ 0, то у системы есть только одно решение, которое можно получить методом обратной матрицы, если же det A = 0, то такая система методом обратной матрицы не решается.
Решение обратной матрицы.
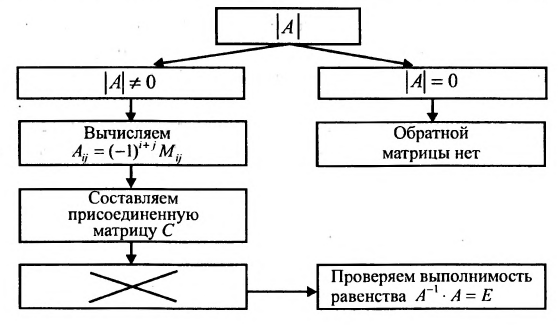
Последовательность действий для решения обратной матрицы:
Приведенный ниже алгоритм решения обратной матрицы по сути такой же, как и приведенный выше, разница только в нескольких шагах: первым делом определяем алгебраические дополнения, а уже после этого вычисляем союзную матрицу C.
Нахождение обратной матрицы.
Нахождение обратной матрицы – это лучше всего делать с помощью присоединённой матрицы.
Теорема: Если к квадратной матрице с правой стороны приписать единичную матрицу такого же порядка и при помощи элементарных преобразований над строками преобразовать начальную матрицу, стоящую слева, в единичную, то полученная с правой стороны будет обратной к начальной.
Пример нахождения обратной матрицы.
Задание. Для матрицы 
найти обратную методом присоединенной матрицы.
Решение. Дописываем к заданной матрице А справа единичную матрицу 2го порядка:
Из 1й строки вычитаем 2ю:
От второй строки отнимаем 2 первых:
1ю и 2ю строки меняем местами:
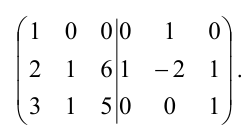
От 2й строки отнимаем 2 первых:
Вторую строку умножаем на (-1), а к первой строке добавляем 2ю:
Итак, слева имеем единичную матрицу, а, значит, матрица, которая стоит справа, будет обратной к заданной изначально.
Т.о., имеем 
.
Ответ после нахождения обратной матрицы:
Замечание. Если на каком-либо этапе в «левой» матрице образуется нулевая строка, значит, что заданная изначально не имеет обратной.
Содержание:
Теоремы существования и единственности обратной матрицы:
Рассмотрим квадратную матрицу:
Определение 4.1.1. Матрица, которая в результате умножения на матрицу А, равна единичной матрице Е, называется обратной А и обозначается 
.
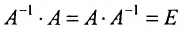
Отметим, что если А и В квадратные матрицы одного порядка, то определитель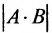 
произведения матриц равен произведению
определителей множителей
Теорема 4.1.1. (теорема существования). Для существования обратной матрицы необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы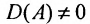 
.
Доказательство. Необходимость. Пусть обратная матрица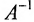 
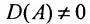
существует. Докажем, что 
.
Так как обратная матрица существует, то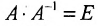 
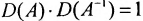
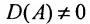
и 
.Поскольку правая часть не равна нулю, то ни один из множителей левой части не может быть равен нулю. Следовательно 
, что означает, что матрица A невырожденная.
Достаточность. Пусть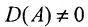 
, докажем, что обратная матрица существует.
Вычислим алгебраические дополнения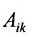 
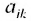
каждого элемента 
в определителе D(A). Из полученных алгебраических дополнений построим матрицу:
Матрица С называется союзной, или присоединенной, по отношению к матрице А, причем в i-й строке союзной матрицы С стоят алгебраические дополнения элементов i-го столбца матрицы А. Составим произведение матриц С и А, тогда элемент произведения, стоящий в i-й строке и k-м столбце, равен 
. На основании теоремы разложения сумма произведений элементов определителя на их алгебраические дополнения равна величине определителя. А сумма парных произведений какого-нибудь ряда определителя на алгебраические дополнения параллельного ряда равна нулю (см. теорему аннулирования). Значит, все недиагональные элементы матрицы АС равны нулю, а диагональные равны D(A), следовательно:
(4.1.1)
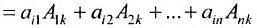
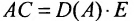
Так как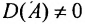 
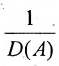
, то равенство (4.1.1) можно умножить на скаляр 
. Получим:
Тогда матрица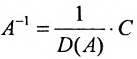 
будет обратной для матрицы А. Теорема доказана.
Сформулируем алгоритм нахождения обратной матрицы:.
Этот алгоритм можно представить в виде следующей схемы:
Теорема 4.1.2. (теорема единственности). Для каждой неособенной матрицы А существует единственная обратная матрица.
Доказательство. Допустим, что наряду с обратной матрицей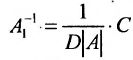 
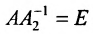
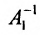
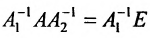
существует другая обратная матрица 
. Тогда по определению 
. Умножая обе части этого равенства слева на 
, получим 
.
Поскольку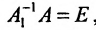 
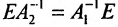
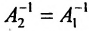
, то
, а это значит, что 
. Теорема доказана.
Вычислив определители левой и правой частей равенства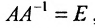 
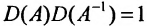
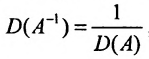
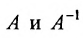
, получим 
, следовательно 
то есть определители матриц 
взаимно обратные.
Замечание. Формула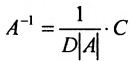 
позволяет найти явные выражения для элементов обратной матрицы через элементы матрицы А (см. алгоритм 1). Однако построение союзной матрицы очень трудоемкая операция при больших размерностях матриц. Поэтому доказанная формула, в большей мере, важна в теоретическом отношении.
Свойства обратной матрицы. Подобная матрица
Укажем некоторые свойства обратной матрицы:
Понятие обратной матрицы позволяет ввести следующее определение:
Определение 4.2.1. Квадратная матрица А называется подобной матрице В, если существует невырожденная матрица Т, для
которой выполняется равенство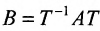 
.
Говорят, что матрица А трансформируется в матрицу В при помощи матрицы Т.
Отношение подобия обладает тремя основными свойствами:
Приложения обратной матрицы в экономических исследованиях
Применение обратных матриц в экономических исследованиях столь многочисленно и разнообразно, что мы приведём отдельные примеры использования обратной матрицы в экономических исследованиях.
Пример:
Предположим, что затраты времени оборудования при выпуске изделий пропорциональны количеству готовых изделий и пусть известна квадратная матрица Т норм затрат времени оборудования на различные изделия на различных типах оборудования. Если задана матрица-столбец А затрат времени на различных типах оборудования, необходимое для выполнения производственной профаммы, то определение возможного выпуска готовых изделий X осуществляется с использованием обратной матрицы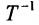 
:
Валовой выпуск продукции X также можно определить, зная матрицу Z норм затрат рабочего времени рабочих различных категорий и фонд рабочего времени F по категориям рабочих, вычислив произведение обратной матрицы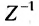 
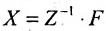
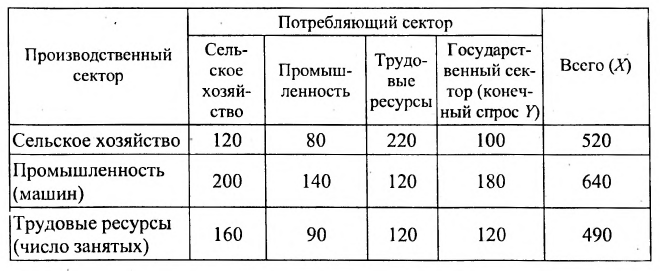
на F, т.е. 
.
Пример:
Сумма показателей в строках даёт общий выпуск каждой отрасли и суммарное число занятых. Суммы показателей по столбцам показывают затраты данного сектора, необходимые для производства всего объёма продукции. Следовательно, каждый столбец описывает производственную функцию данного сектора. Так, например, первый столбец характеризует основной производственный процесс, который в текущем периоде применяется в сельском хозяйстве. Для производства 520 т продукции сельского хозяйства требуется 120 т сельскохозяйственной продукции, 200 машин и 160 работников. Определим валовой выпуск продукции для конечного спроса, определяемого матрицей-столбцом: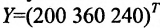 
.
Решение:
Пусть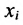 
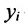
— валовой выпуск продукции i,i=1,2,3; а 
-конечный спрос на продукцию /. Валовой выпуск каждого вида продукции должен быть равен сумме продукции, использованной при производстве всех видов продукции, плюс конечный спрос на эту же продукцию:
где
— количество продукции i, используемое при производстве единицы продукции j. В матричном обозначении получим: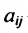
где X, Y- матрицы столбцы, а А- матрица коэффициентов прямых затрат. Все её элементы неотрицательны.
. (4.3.2)
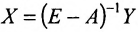
Далее вычисляем элементы матрицы Е-А: 
вычисляем определитель 
и алгебраические дополнения элементов матрицы (Е-А):
Составляем из алгебраических дополнений присоединённую матрицу С:
и вычисляем элементы обратной матрицы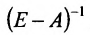 
:
Тогда в силу (4.3) находим валовой выпуск продукции: 
Таким образом, для удовлетворения новых показателей спроса необходимо будет произвести приблизительно 1042 т продукции сельского хозяйства, 1280 машин и нанять 1119 работников.
Особенности матриц в ценностном и натуральном выражении
Матрица коэффициентов прямых материальных затрат А, рассмотренная нами в примере предыдущего пункта, относится к классу неотрицательных матриц, так как матрица-столбец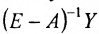 
должна быть неотрицательна.
Определение 4.4.1. Если решение системы (4.3.1) сществует для любой неотрицательной матрицы Y конечного спроса, то матрица А называется продуктивной.
Поэтому элементы матрицы А не могут принимать произвольные положительные значения. Все диагональные элементы матрицы А должны быть меньше единицы. В противном случае производство лишается всякого смысла (если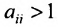 
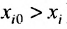
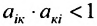
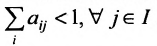
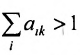
, то 
). Произведение коэффициентов, симметричных относительно главной диагонали, должно быть также меньше единицы: 
. Указанные ограничения на значения элементов матрицы А не зависят от единиц измерения. Однако в общем случае выбор единиц измерения существенно влияет на анализ свойств матриц межотраслевого баланса. Для матриц межотраслевого баланса в ценностном выражении обычно выполняются условия 
• Если же для некоторой k-и отрасли 
, то экономически это означает, что данная отрасль настолько убыточна, что её убытки перекрывают расходы на амортизацию и оплату труда.
Так как норму матрицы А можно определить по формуле
, то при условии что 
норма матрицы А меньше единицы, т.е. 
.
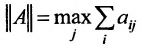
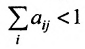
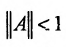
Если норма матрицы А меньше единицы, то
Отметим, что в матрицах межотраслевого баланса в натуральном выражении условия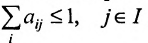 
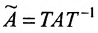
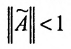
, практически никогда не выполняются. Более того, многие элементы этих матриц больше единицы. Однако можно подобрать такие новые измерители (матрицу T), что для подобной матрицы 
будет выполняться 
и следствия из него.
Подобные матрицы имеют равные по величине собственные значения и главные миноры;
Для продуктивности матрицы А необходимо и достаточно, чтобы выполнялось одно из приведенных ниже условий:
Условие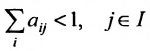 
является достаточным для продуктивностн матрицы А.
Матрица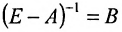 
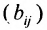
называется матрицей коэффициентов полных затрат, а её элементы- коэффициентами полных затрат. Они 
показывают, какой должен быть валовой выпуск i-Й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта j-й отрасли.
Коэффициенты полных затрат 
не меньше коэффициентов прямых затрат: 
так как они характеризуют совокупность прямых и косвенных затрат.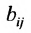
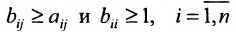
Вернёмся к примеру 1.12 и проанализируем матрицы коэффициентов прямых затрат А и полных затрат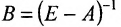 
:
Элементы матрицы А удовлетворяют условиям:
4) норма матрицы 
Значит матрица А является продуктивной и для неё существует обратная матрица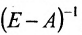 
, называемая матрицей полных затрат.
Из вида матрицы В следует, что все коэффициенты полных затрат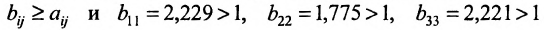 
. Например, элементы первого столбца матрицы В показывают, что для того чтобы произвести единицу конечной продукции сельского хозяйства нужно произвести 2,222 единиц сельского хозяйства, 1,766 единиц промышленности и занять 1,845 работников.
Определение обратной матрицы
Рассмотрим квадратную матрицу
Обозначим 
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если 
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение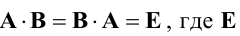 
— единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через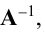 
так что
Обратная матрица вычисляется по формуле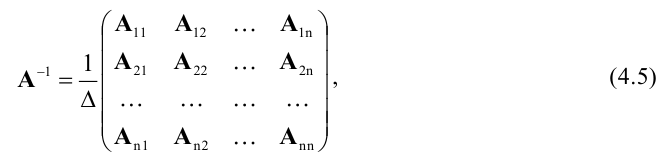 
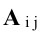
где 
— алгебраические дополнения элементов 
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример:
Для матрицы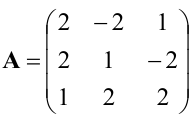 
найти обратную.
Решение:
Находим сначала детерминант матрицы А:
значит, обратная матрица существует и мы ее можем найти по формуле: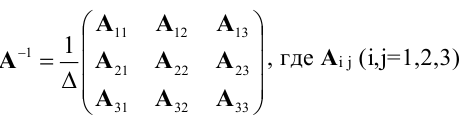 
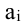
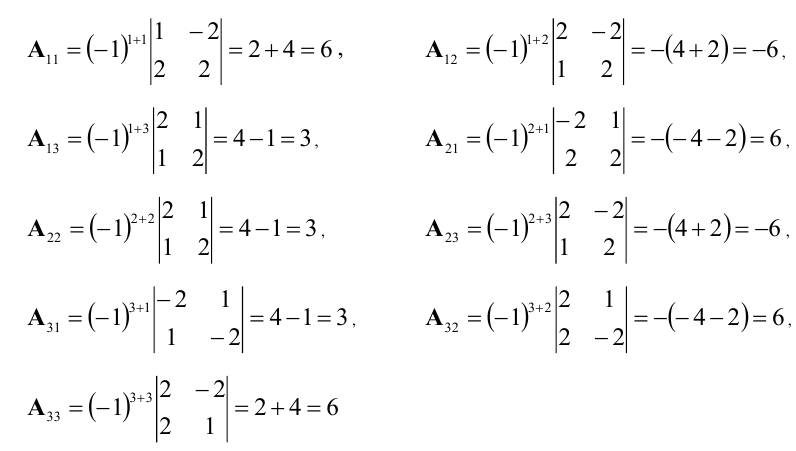
— алгебраические дополнения элементов 
исходной матрицы. 
откуда 
Пример:
Методом элементарных преобразований найти обратную матрицу для матрицы: 
Решение:
Приписываем к исходной матрице справа единичную матрицу того же порядка: 
С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей. Для этого поменяем местами первый и второй столбцы: 
Прибавим третий столбец к первому и второму: 
Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак, 
Что такое обратная матрица и как её решать
Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной.
Диагональная матрица, элементы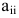 
которой равны единице, называется единичной матрицей. Обозначение: Е.
Внимание! Обратная матрица существует только для невырожденной квадратной матрицы.
Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. В противном случае матрица называется вырожденной.
Теорема:
Для невырожденной матрицы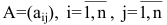 
существует единственная обратная матрица
где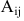 
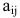
— алгебраические дополнения элементов 
матрицы А.
Пример:
Найти матрицу X из матричного уравнения АХ=В, где 
Решение:
Умножим уравнение АХ=В на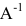 
слева:
Найдем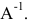 
Обратная матрица к А существует, т.к. матрица А невырожденная:
Вычислим алгебраические дополнения элементов матрицы А:
Произведение матриц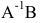 
существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно 3. Найдем его: 
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.