Обратно квадратичная зависимость тока что это

Закон обратных квадратов

СОДЕРЖАНИЕ

Формула [ править ]

Математические обозначения (см. ∝ ):

интенсивность ∝ 1 расстояние 2 <\ displaystyle <\ text <интенсивность>> \ \ propto \ <\ frac <1><<\ text > ^ <2>>> \,>

Математически это также можно выразить как:

интенсивность 1 интенсивность 2 знак равно расстояние 2 2 расстояние 1 2 <\ displaystyle <\ frac <<\ text <интенсивность>> _ <1>> <<\ text <интенсивность>> _ <2>>> = <\ frac <<\ text > _ <2>^ <2>> <<\ text > _ <1>^ <2>>>>

или как формулировка постоянной величины:

интенсивность 1 × расстояние 1 2 знак равно интенсивность 2 × расстояние 2 2 <\ displaystyle <\ text <интенсивность>> _ <1>\ times <\ text > _ <1>^ <2>= <\ text <интенсивность>> _ <2>\ times <\ text > _ <2>^ <2>>

Обоснование [ править ]

События [ править ]

Гравитация [ править ]

Сила гравитационного притяжения между двумя точечными массами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Сила всегда притягательна и действует по соединяющей их линии. [ необходима цитата ]

Электростатика [ править ]

Свет и другое электромагнитное излучение [ править ]

В фотографии и сценическом освещении закон обратных квадратов используется для определения «спада» или разницы в освещении объекта, когда он приближается к источнику света или дальше от него. Для быстрого приближения достаточно помнить, что удвоение расстояния уменьшает освещенность на четверть; [9] или аналогично, чтобы уменьшить вдвое освещенность, увеличьте расстояние в 1,4 раза ( квадратный корень из 2 ), а для удвоения освещенности уменьшите расстояние до 0,7 (квадратный корень из 1/2). Когда источник света не является точечным источником, правило обратных квадратов часто по-прежнему является полезным приближением; когда размер источника света составляет менее одной пятой расстояния до объекта, ошибка вычисления составляет менее 1%. [10]

Пример [ править ]

Энергия или интенсивность уменьшаются (делятся на 4) по мере удвоения расстояния r ; при измерении в дБ уменьшится на 3,01 дБ при удвоении расстояния. При обращении к измерениям мощности величин, соотношение может быть выражено как уровень в децибелах путем оценки в десять раз по основанию 10 логарифм отношения измеряемой величины к опорному значению.

Звук в газе [ править ]

Интерпретация теории поля [ править ]

при условии, что пространство за пределами источника не имеет расхождений. [ необходима цитата ]

История [ править ]

Джон Дамблтон из Oxford Calculators XIV века был одним из первых, кто выразил функциональные взаимосвязи в графической форме. Он представил доказательство теоремы о средней скорости, в которой говорится, что «широта равномерно дифференцированного движения соответствует степени средней точки», и использовал этот метод для изучения количественного уменьшения интенсивности освещения в своей « Summa logicæ et Философский натуралист» (ок. 1349), заявив, что оно не было линейно пропорционально расстоянию, но не смогло раскрыть закон обратных квадратов. [11]

В предложении 9 книги 1 в своей книге Ad Vitellionem paralipomen, quibus astronomiae pars optica traditur (1604 г.) астроном Иоганн Кеплер утверждал, что распространение света от точечного источника подчиняется закону обратных квадратов: [12] [13]

Оригинал: Sicut se habent spharicae superificies, quibus origo lucis pro centro est, ampior ad angustiorem: ita se habet fortitudo seu densitas lucis radiorum in angustiori, ad illamin in laxiori sphaerica, hoc est, converim. Nam per 6. 7. tantundem lucis est in angustiori sphaerica superficie, Quantum in fusiore, tanto ergo illie stipatior & densior quam hic.

Перевод : Подобно тому, как [соотношение] сферических поверхностей, для которых источником света является центр, [является] от более широкого к более узкому, так и плотность или стойкость лучей света в более узком [пространстве] по направлению к более просторные сферические поверхности, то есть наоборот. Поскольку согласно [предложениям] 6 и 7, в более узкой сферической поверхности столько же света, сколько в более широкой, поэтому здесь он гораздо более сжат и плотнее, чем там.

Оригинал: Virtus autem illa, qua Sol prehendit seu harpagat planetas, corporalis quae ipsi pro manibus est, lineis rectis in omnem mundi ampitudinem emissa quasi views solis cum illius corpore rotatur: cum ergo sit corporalis imminuitur, & extenuatur in maiorlo sp. autem huius imminutionis eadem est, ac luminus, in ratione nempe dupla intervallorum, sed eversa.

В Англии англиканский епископ Сет Уорд (1617–1689) опубликовал идеи Буллиалдуса в своей критике в «Ismaelis Bullialdi astronomiae philolaicae Fundmenta inquisitio brevis» (1653) и опубликовал планетарную астрономию Кеплера в своей книге Astronomia geometrya (1656).

В 1663–1664 годах английский ученый Роберт Гук писал свою книгу « Микрография».(1666), в котором он обсуждал, среди прочего, связь между высотой атмосферы и барометрическим давлением на поверхности. Поскольку атмосфера окружает Землю, которая сама по себе является сферой, объем атмосферы, имеющий отношение к любой единице площади земной поверхности, представляет собой усеченный конус (который простирается от центра Земли до космического вакуума; очевидно, только часть конуса от земной поверхности до космических медведей на земной поверхности). Хотя объем конуса пропорционален кубу его высоты, Гук утверждал, что давление воздуха у поверхности земли вместо этого пропорционально высоте атмосферы, потому что сила тяжести уменьшается с высотой. Хотя Гук прямо об этом не заявлял,соотношение, которое он предложил, будет верным только в том случае, если сила тяжести уменьшается как обратный квадрат расстояния от центра Земли. [17] [18]

См. Также [ править ]

Ссылки [ править ]

Источник

Среднеквадратичное (действующее, эффективное) значение

Лампочка и постоянное напряжение

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт

Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I — сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.

Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

Подаем напряжение с блока питания на лампу и вуаля!

К этим же клеммах цепляем и наш осциллограф

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

Замеряем силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку 😉

Лампочка и переменное напряжение

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Среднеквадратичное значение напряжения

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение зажигали одну и ту же лампочку, которая кушала одну и ту же мощность. Значит эта осциллограмма

и вот эта осциллограмма

Чем то похожи? Но чем.

Среднеквадратичное значение напряжения — это такое значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении. То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном. То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала любой частоты равняется максимальной его амплитуде, поделенной на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то U_max = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение. Максимальная амплитуда этих 220 Вольт равняется 220х1,41=310 Вольт.

Где же среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот же они!

Vk — это и есть среднеквадратичное напряжение этого сигнала.

Ma — это и есть Umax.

Конечно, 16,6/1,41=11,8 Вольт, а он пишет 12,08 Вольт.

Источник

Среднеквадратичное значение тока

Физика > Среднеквадратичное значение корня

Изучите соотношение среднеквадратичного напряжения и тока – формула и как найти. Читайте определение среднеквадратичного значения, применение, уравнения.

Среднеквадратичное напряжение или ток – усредненное по времени напряжение или ток в системе переменного тока.

Задача обучения

Основные пункты

Термин

Среднеквадратичное значение и переменный ток

В ситуациях с переменным током поток электрического заряда периодически меняет направление. Если в постоянном ток и напряжение остаются стабильными, то здесь они меняются со временем. Этот вариант используют по большей части в быту. Иногда возникает необходимость узнать усредненный по времени показатель тока или напряжения. Для этого можно взять средний квадрат корня со временем.

Определение

Соответствующая формула для непрерывной функции f (t), вычисленной на интервале T₁ ≤ t ≤ T₂:

Среднеквадратичное значение тока для функции в течение всего времени:

Среднеквадратичное значение напряжения за время периодической функции приравнивается к СКЗ одного периода.

Применение к напряжению и току

Давайте взглянем на синусоидально меняющееся напряжение:

(а) – Постоянное напряжение и ток остаются стабильными. (b) – График напряжения и тока в зависимости от времени для мощности переменного тока в 60 Гц. Напряжение и ток выступают синусоидальными и расположены в фазе для простой схемы сопротивления. Частоты и пиковые напряжения сильно отличаются

V = V₀sin (2πft), где V – напряжение в момент времени, V₀ – пиковое напряжение, f – частота в Гц. Для этой простой схемы сопротивления I = V/R, поэтому ток переменного выглядит как:

I = I₀sin (2πft), где I – ток в момент времени, а I₀ = V₀/R – пиковый ток. Теперь, используя вышеприведенное определение, выведем среднеквадратичные напряжение и ток. Прежде всего, у нас есть

Здесь мы заменили 2πf на ω. Поскольку V₀ выступает постоянной, можно разложить ее из квадратного корня и использовать тригонометрическую формулу для замены квадрата синусоидальной функции.

Поскольку интервал отображает целое число полных циклов, члены отменяются, оставляя:

Вы также поймете, что СКЗ можно выразить через

Обновленное уравнение контура

Многие из выведенных уравнений относятся к переменному току. Если нам нужно получить усредненный по времени результат, то соответствующие переменные выражаются в СКЗ. К примеру, закон Ома передается как

Различные выражения для мощности переменного тока выглядят как:

Отсюда видно, что можно вывести среднюю мощность, основываясь на пиковом напряжении и токе.

Мощность переменного тока, основываясь на времени. Напряжение и ток пребывают в фазе, а их продукт колеблется между нулем и I₀V₀. Средняя мощность – (1/2) I₀V₀

СКЗ полезны, если напряжение меняется по форме сигнала, отличающегося от синусоидов (квадратные, треугольные или пилообразные волны).

Синусоидальные, квадратные, треугольные и пилообразные волны

Источник

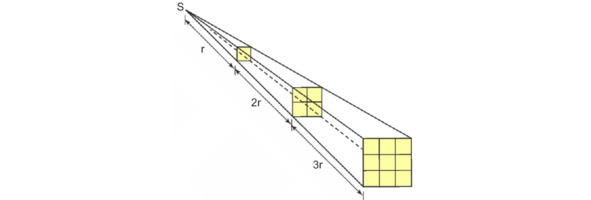
1.7. Законы обратных квадратов

Рис. 1.2. Закон обратных квадратов. Интенсивность света обратно пропорциональна квадрату расстояния от источника (S).

Проанализируем аналогичные законы, известные физике, в знаменателе которых стоит квадрат расстояния. Будем уповать на то, что в начале XXI в. ключевые законы физики действительно открыты и известны. Поэтому нужно внимательно посмотреть на все это законное хозяйство под определенным углом зрения, а именно – под прицелом гравитации.

В свое время еще И. Кантом было замечено, что законы обратных квадратов для гравитационной и электростатической сил связаны с 3-мерностью пространства.

Закон обратных квадратов – закон, согласно которому некая физическая величина в определенной точке обратно пропорциональна квадрату расстояния до этой точки. Суть таких законов в том, что данная физическая величина распространяется из центра равномерно во все стороны пространства.

Обратно квадратичной зависимости подчиняются следующие физические законы:

• Звуковые волны от точечного (шарового) источника звуков

• Напряженность электрического поля Е на расстоянии r от точечного заряда Q в вакууме (закон Кулона)

• Напряженность магнитного поля (закон Био—Савара—Лапласа)

• Освещенность Е_п плоской поверхности, создаваемая точечным источником света

• Напряженность гравитационного поля (закон Ньютона)

Вот основной набор уравнений волнового излучения, подчиняющихся закону обратных квадратов.

Проведем анализ указанных законов и попробуем их отождествить с гравитационным взаимодействием.

Звуковые волны хороши, но они явно не подходят, так как звук распространяется только в атмосфере (среде), а она, как известно, имеется далеко не у всех небесных тел, не говоря уже о межзвездном пространстве.

Законы Кулона и Био—Савара—Лапласа тоже хороши, но также не подходят под тождество с гравитационным взаимодействием. Электрические и магнитные силы во много раз превосходят гравитационные. Радиус действия этих сил также не сопоставим – электромагнитные силы действуют на более коротких расстояниях. Оставим пока в покое и эти законы.

Остается что? Остается – свет! Чтобы не забыть, так и запишем: гравитация – это свет!

На квантовом уровне свет у нас представляет фотон, а гравитацию – гипотетический гравитон.

Приравняем кванты фотона ? и гравитона g.

На такое скоропалительное заключение кто-то интеллигентно скажет: «Некорректное отождествление», а кто-то резко: «Чушь!» Но не будем так категоричны и продолжим построение логической цепочки.

Свет, безусловно, хорош, и о нем мы знаем практически все. Опыты со светом проводились еще в древности. Оптическое излучение (свет) представляет собой электромагнитное излучение с длиной волны от 0,01 нм до 0,1 мм. Свет подчиняется законам оптики, а оптика, по накопленным наблюдениям и опыту, еще более древняя наука, чем механика.

Давайте посмотрим на это физическое явление оптическим глазом еще раз и более внимательно. Что может роднить свет с гравитацией?

1. 1/r 2 – общий знаменатель? И это все? Хотя, просматривая глубже, находим еще несколько соответствий.

2. Скорости распространения электромагнитной световой волны и гравитационной волны равны: с=2.998·10 8 м/с (скорость света в вакууме).

3. Свет и гравитация распространяются волнообразно. А, как известно, волны являются переносчиками энергии. Без энергии нет движения, без движения нет энергии.

4. Гравитоны идентичны фотонам, их массы связаны только с движением – масса покоя как таковая у данных частиц отсутствует.

5. Фотон – квант электромагнитного поля, гравитон – гипотетический квант гравитационного поля. Квант – это некая минимальная частичка энергии.

6. Фотоны и гравитоны не избирательны к воспринимающим их объектам. Они не поляризованы и не заряжены, им безразлично внутреннее состояние вещества, тела или предмета, они равнозначно взаимодействуют со всеми.

Шесть соответствий – это уже не то что серьезно, а вполне достаточно, чтобы отождествить фотоны с гравитонами. Или недостаточно?

Вот этим и займемся в ближайшем постраничном пространстве. А для этого заглянем еще глубже, а точнее дальше, где мы должны увидеть свет не только в конце тоннеля, но и в далеком Космосе. Гравитация, похоже, действует таким же образом, разница только в одном: свет мы видим всегда, а гравитацию – никогда!

Вот написал последнюю фразу и усомнился в ее правильности. Сами фотоны, как переносчики света, мы тоже не видим. Как можно увидеть фотоны, проскакивающие мимо нас со скоростью чего? – того самого света! Мы видим реакцию этого света с окружающими нас предметами, поэтому нас ни на секунду не покидает ощущение его присутствия. Свет либо отражается от них, тогда мы видим блестящую или зеркальную поверхность, либо поглощается ими, тогда видим оттенки серого. По сути, мы не видим отдельные фотоны, а только их интегральное действие на сетчатку глаза. Чтобы увидеть свет, необходимо действие 200 фотонов в секунду [12, с. 46]. Итак, седьмое соответствие.

7. Одиночные фотоны света и гравитоны не видимы зрением!

Что касается источников света, например, скептики сразу мне возразят: «Ты что, слепой, и Солнце не видишь?» На что я спокойно отвечу: «Я вижу Солнце, оно испускает световые волны, я также отчетливо вижу, что оно испускает и гравитационные волны, а вы что, их не видите? Тогда вы невесомы!»

Так кто из нас прав?

Гравитационную энергию переносят все волны, а мы видим только в узком промежутке 780—380 нм (3?10 14 – 4?10 14 Гц) из всей шкалы широкого диапазона электромагнитных волн.

Получается, свет загораживает нам гравитационную картину.

Пока не поздно, можно отмахнуться от гравитации известным выражением: «То, что не вижу, для меня не существует!», но не будем спешить, не для того затеян разбор гравитационных полетов.

Здесь следует напомнить, что солнечный свет или свет от обычной лампы накаливания содержит полный спектр длин волн, который распадается на составляющие при прохождении его через стеклянную призму. «Каждый охотник желает знать…» – получается радуга, которую в искусственных условиях исследовал И. Ньютон и многие другие физики.

Электромагнитные волны представляют собой периодические колебания электрических и магнитных полей, распространяющиеся в среде или вакууме. Для распространения таких волн не требуется наличия какой-либо среды.

Данный текст является ознакомительным фрагментом.

Источник