Обратная связь между переменными предполагает что
Корреляция и коэффициент корреляции
Корреляция — степень связи между 2-мя или несколькими независимыми явлениями.
Корреляция бывает положительной и отрицательной.
Положительная корреляция (прямая) возникает при одновременном изменении 2-х переменных величин в одинаковых направлениях (в положительном или отрицательном). Например, взаимосвязь между количеством пользователей, приходящих на сайт из поисковой выдачи и нагрузкой на сервер: чем больше пользователей, тем больше нагрузка.
Корреляция отрицательна (обратная), если изменение одной величины приводит противоположному изменению другой. Например, с увеличением налоговой нагрузки на компании уменьшается их прибыль. Чем больше налогов, тем меньше денег на развитие.

Эффективность корреляции как статистического инструмента заключается в возможности выражения связи между двумя переменными при помощи коэффициента корреляции.
При значении КК равным 1, следует понимать, что при каждом изменении 1-й переменной происходит эквивалентное изменение 2-й переменной в том же направлении.


| Значение | Интерпретация |
| до 0,2 | Очень слабая |
| до 0,5 | Слабая |
| до 0,7 | Средняя |
| до 0,9 | Высокая |
| свыше 0,9 | Очень высокая корреляция |
Данный метод обработки статистической информации популярен в экономических, технических, социальных и других науках в виду простоты подсчета КК, простотой интерпретации результатов и отсутствия необходимости владения математикой на высоком уровне.
Корреляционная зависимость отражает только взаимосвязь между переменными и не говорит о причинно-следственных связях: положительная или отрицательная корреляция между 2-мя переменными не обязательно означает, что изменение одной переменной вызывает изменение другой.
Например, есть положительная корреляция между увеличением зарплаты менеджеров по продажам и качеством работы с клиентами (повышения качества обслуживания, работа с возражениями, знание положительных качеств продукта в сравнении с конкурентами) при соответствующей мотивации персонала. Увеличившийся объем продаж, а следовательно и зарплата менеджеров, вовсе не означает что менеджеры улучшили качество работы с клиентами. Вполне вероятно, что случайно поступили крупные заказы и были отгружены или отдел маркетинга увеличил рекламный бюджет или произошло еще что-то.
Возможно существует некая третья переменная, влияющая на причину наличия или отсутствия корреляции.
Коэффициент корреляции не рассчитывается:
Понятие о функциональной и корреляционной связи



1. Регрессионный анализ.
2. Корреляционно-регрессионный анализ.
3. Понятие о функциональной и корреляционной связи.
Независимыми,или факторными, называют признаки, которые вызывают изменения других, связанных с ними признаков. Признаки, изменение которых под воздействием определенных факторов требуется проследить, называют зависимыми, или результативными.
При функциональной связи изменение независимых переменных приводит к получению точно определенных значений зависимой переменной.
Наиболее часто функциональные связи проявляются в естественных науках, например в механике функциональной является зависимость расстояния, пройденного объектом, от скорости его движения и т. п.
При статистической связи каждому значению независимой переменной Х соответствует множество значений зависимой переменной Y, причем не известно заранее, какое именно. Например, мы знаем, что прибыль коммерческого банка определенным образом связана с размером его уставного капитала (этот факт не подлежит сомнению). Тем не менее, нельзя вычислить точную величину прибыли при заданном значении последнего показателя, так как она зависит еще и от множества других факторов, помимо размера уставного капитала, среди которых имеются и случайные. В нашем случае, скорее всего, мы определим лишь среднее значение прибыли, которое будет получено в целом по совокупности банков со сходным объемом уставного капитала. Таким образом, статистическая связь отличается от функциональной наличием действия на зависимую переменную большого числа факторов.
Заметим, что статистическая связь проявляется лишь «в общем и среднем» при большом числе наблюдений за явлением. Так, интуитивно мы можем предполагать, что существует зависимость между объемом основных фондов предприятия и получаемой им прибылью, а именно с увеличением первого размер прибыли возрастает. Но на это можно возразить и привести пример предприятия, обладающего достаточным количеством современного производственного оборудования, но тем не менее терпящего убытки. В данном случае мы имеем наглядный пример статистической связи, которая проявляется лишь в больших совокупностях, содержащих десятки и сотни единиц в отличие от функциональной, подтверждающейся для каждого наблюдения.
Корреляционной является статистическая связь между признаками, при которой изменение значений независимой переменной Х приводит к закономерному изменению математического ожидания случайной величины Y.
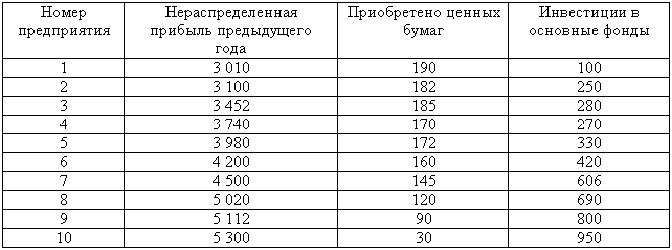
Пример 8.1 – Предположим, что имеются данные по предприятиям о размере нераспределенной прибыли предыдущего года, объеме инвестиций в основной капитал и о суммах, выделенных на приобретение ценных бумаг (тыс. ден. ед.) – таблица 8.1.
Таблица 8.1 – Основные показатели деятельности предприятий
Проведение корреляционно-регрессионного анализа предполагает решение следующих задач:
1) выявление из большого числа факторов наиболее информативных, оказывающих более существенное воздействие на результативную величину (предварительный анализ, базирующийся на простейших методах выявления зависимостей и экспертных оценках);
2) определение направления и количественной оценки тесноты зависимости между факторной величиной Х и результативной Y (при этом факторных переменных может быть достаточно много, тогда определяется множественная корреляция);
3) нахождение математической функции, описывающей зависимость результативного показателя Yот наиболее информативных факторных Х. Эта функция выполняет роль модели, которая аналитически выражает зависимость условного среднего значения результативного признака от факторных переменных
4) оценка качества полученной модели, определение возможной величины ошибки получаемых по этой модели прогнозных значений Y;
5) построение прогнозов.
Тема 11 Причинность, регрессия, корреляция
Причинность, регрессия, корреляция
Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения ‑ это такая связь явлений и процессов, когда изменение одного из них ‑ причины ведет к изменению другого ‑ следствия.
Финансово-экономические процессы представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих процессов необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.
В основе первого этапа статистического изучения связи лежит качественный анализ, связанный с анализом природы социального или экономического явления методами экономической теории, социологии, конкретной экономики.
Второй этап – построение модели связи, базируется на методах статистики: группировках, средних величинах, и так далее.
Третий, последний этап ‑ интерпретация результатов, вновь связан с качественными особенностями изучаемого явления. Статистика разработала множество методов изучения связей. Выбор метода изучения связи зависит от познавательной цели и задач исследования.
Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса.
Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами.
Признаки, изменяющиеся под действием факторных признаков, называются результативными.
В статистике различают функциональную и стохастическую зависимости.
Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
Таблица 11.1. ‑ Количественные критерии оценки тесноты связи
Величина показателя связи
По направлению выделяют связь прямую и обратную.
Прямая ‑ это связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака.
Пример. Так, рост объемов производства способствует увеличению прибыли предприятия.
В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака, то есть обратная ‑ это связь, при которой с увеличением или с уменьшением значений одного признака происходит уменьшение или увеличение значений другого признака.
Пример. Так, снижение себестоимости единицы производимой продукции влечет за собой рост рентабельности.
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные.
Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида:
Если же связь может быть выражена уравнением какой-либо кривой, то такую связь называют нелинейной или криволинейной, например:
Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных; графический; аналитических группировок; корреляции, регрессии.
Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.
Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат ‑ результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.
В статистике принято различать следующие виды зависимостей:
Корреляционный анализ имеет своей задачей количественное определение тесноты и направления связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии. Знаки при коэффициентах корреляции характеризуют направление связи между признаками.
Регрессия тесно связана с корреляцией и позволяет исследовать аналитическое выражение взаимосвязи между признаками.
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком), обусловлено влиянием одной или нескольких независимых величин (факторных признаков).
Одной из проблем построения уравнений регрессии является их размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным. Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время, построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.
При построении моделей регрессии должны соблюдаться требования:
Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные социально-экономические явления и процессы.
Парная регрессия на основе метода наименьших квадратов позволяет получить аналитическое выражение связи между двумя признаками: результативным и факторным.
Определить тип уравнения можно, исследуя зависимость графически, однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи ‑ гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
где п ‑ объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр ао показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а1 показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения. xi – теоретические значения результативного признака; yi – наблюдаемые значения факторного признака.
Пример. Имеются данные по 10 однотипным предприятиям о выпуске продукции (х) в тыс.ед. и о расходе условного топлива (у) в тоннах (графы 1 и 2 табл. 17).
Требуется найти уравнение зависимости расхода топлива от выпуска продукции (или уравнение регрессии у по х) и измерить тесноту зависимости между ними. Для этого представим данные в табл. 11.2 (вместе с расчетными столбцами).
Таблица 11.2 – Расчет показателей для нахождения уравнения регрессии
| № п/п | Выпуск продукции, xi,тыс.ед. | Расход топлива, yi, тонн |  | |||
| 1 | 5 | 4 | 25 | 20 | 16 | 3,9 |
| 2 | 6 | 4 | 36 | 24 | 16 | 4,4 |
| 3 | 8 | 6 | 64 | 48 | 36 | 5,5 |
| 4 | 8 | 5 | 64 | 40 | 25 | 5,5 |
| 5 | 10 | 7 | 100 | 70 | 49 | 6,6 |
| 6 | 10 | 8 | 100 | 80 | 64 | 6,6 |
| 7 | 14 | 8 | 196 | 112 | 64 | 8,8 |
| 8 | 20 | 10 | 400 | 200 | 100 | 12,1 |
| 9 | 20 | 12 | 400 | 240 | 144 | 12,1 |
| 10 | 24 | 16 | 576 | 384 | 256 | 14,3 |
| ∑ * | 125 | 80 | 1961 | 1218 | 770 | 80 |
Необходимые для решения суммы рассчитаны выше в таблице. Подставим их в уравнение и решим систему.
Получив искомое уравнение регрессии можно утверждать, что с увеличение выпуска продукции на тыс. ед., расход топлива возрастет в среднем на 0,547 тонны.
* Если параметры уравнения найдены верно, то
Измерение тесноты (силы) и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака и одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков.
Линейный коэффициент корреляции (К. Пирсона) характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента.
Для измерения тесноты зависимости между у и х применяют линейный коэффициент корреляции, который может быть рассчитан по любой из нижеприведенных формул:
Таблица 11.3 – Оценка линейного коэффициента корреляции




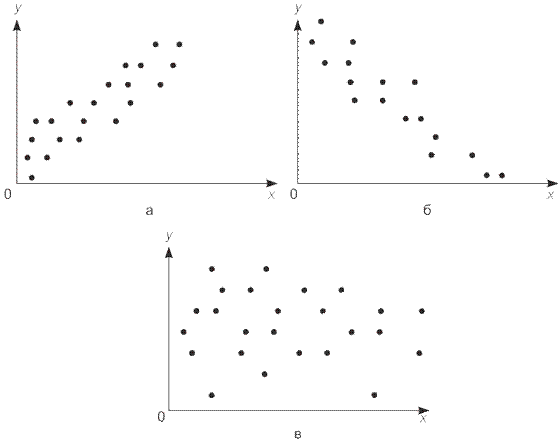
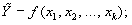

















 означает, что характер связи между исследуемыми признаками прямой.
означает, что характер связи между исследуемыми признаками прямой.