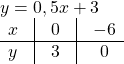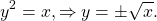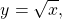Обратная функция для чего нужна
Обратная функция
Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями.
Функции f(x) и g(x) называются взаимно-обратными, если f(g(x)) = x.
Еще один пример взаимно-обратных функций:
Вспомним определение функции. Числовая функция y = f(x) — это такое соответствие между двумя числовыми множествами A и B, при котором каждому числу x ∈ A отвечает одно-единственное число y ∈ B. Множество A называется при этом областью определения функции, множество B — областью значений.
Пусть соответствие f является взаимно-однозначным:
Тогда существует функция g, которая действует в обратную сторону: каждому числу y ∈ B она ставит в соответствие одно-единственное число x ∈ A, такое, что f(x) = y:
Функция g называется обратной к функции f. Точно так же и функция f будет обратной к функции g.
Если мы возьмём какое-либо число x ∈ A и подействуем на него функцией f, то получим число y = f(x) ∈ B. Теперь на полученное число y подействуем функцией g. Куда попадём? Правильно, вернёмся к исходному числу x. Это можно записать так:
 | (1) |
Последовательное применение двух взаимно-обратных действий возвращает нас в исходную точку. Как и в жизни: сначала открыли дверь, а потом совершили обратное действие — закрыли дверь; в итоге вернулись к начальной ситуации.
Так, если возвести число 3 в степень x, а затем совершить обратное действие — взять от полученного числа 3 x логарифм по основанию 3 — мы вернёмся к исходному числу x:
Графики взаимно-обратных функций симметричны относительно прямой у = x.
То, что для функции является областью определения, для обратной функции будет областью значений.
Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции x через у.
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
1) Выражаем из формулы функции x через у. Получаем:
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Взаимно обратные функции, основные определения, свойства, графики
Понятие обратной функции
Для чего вообще нам нужно понятие обратных функций?
Нахождение взаимно обратных функций
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным.
Решение
Обе взаимно обратные функции можно отобразить на графике следующим образом:
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
Решение
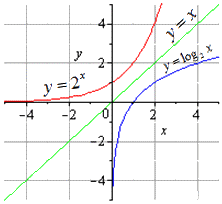
В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
На графике обе функции будут выглядеть так:
Основные свойства взаимно обратных функций
a r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = п о ф о р м у л е п р и в и д е н и я = a r c sin sin π 3 = π 3
Графики взаимно обратных функций
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
Графики для функций с a > 1 и a 1 будут выглядеть так:
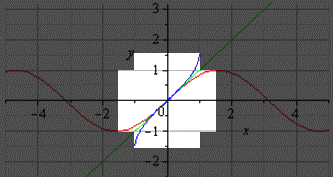
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
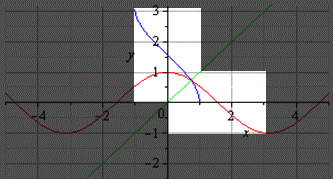
График главной ветви косинуса и арккосинуса выглядит так:
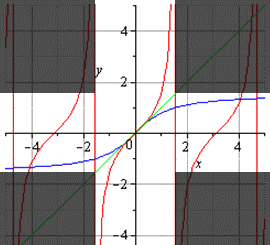
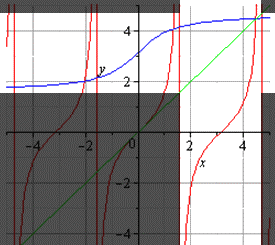
График главной ветви арктангенса и тангенса:
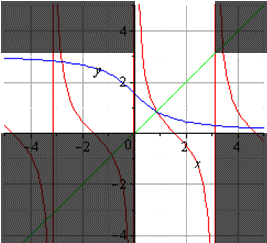
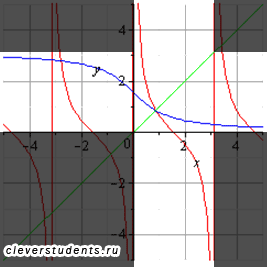
График главной ветви арккотангенса и котангенса будет таким:
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Взаимно обратные функции, основные определения, свойства, графики.
Навигация по странице.
Определение обратной функции.
Пусть функция 
строго монотонная (возрастающая или убывающая) и непрерывная на области определения 
, область значений этой функции 
, тогда на интервале 
определена непрерывная строго монотонная функция 
с областью значений 
, которая является обратной для .
Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений . Решения как раз и записываются через обратные функции.
Примеры нахождения взаимнообратных функций.
Например, требуется решить уравнение 
.
Решениями являются точки 
.
Функции косинус и арккосинус как раз являются обратными на области определения.
Рассмотрим несколько примеров нахождения обратных функций.
Начнем с линейных взаимнообратных функций.
Найти функцию обратную для 
.
Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение относительно x ).
Таким образом, и 
— взаимно обратные функции.
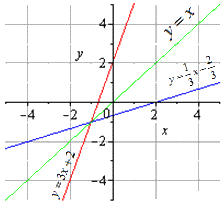
Приведем графическую иллюстрацию взаимно обратных линейных функций.
Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов). Это одно из свойств взаимно обратных функций, о которых речь пойдет ниже.
Теперь рассмотрим пример нахождения логарифмической функции, обратной к заданной показательной функции.
Найти функцию обратную для 
.
Областью определения этой функции является все множество действительных чисел, областью значений является интервал 
. Выразим x через y (другими словами, решим уравнение относительно x ).
Таким образом, и 
— показательная и логарифмическая функции есть взаимно обратные функции на области определения.
График взаимно обратных показательной и логарифмической функций.
Свойства взаимно обратных функций.
Перечислим свойства взаимно обратных функций и .
Замечание по свойству 1).
Рекомендуем ОЧЕНЬ ВНИМАТЕЛЬНО относиться к области определения и области значений функций.
Надеемся, Вы уловили этот тонкий момент.
Особенно аккуратными надо быть с тригонометрическими и обратными тригонометрическими функциями.
К примеру, 
, так как область значений арксинуса 
, а 
в нее не попадает.
Правильно будет
В свою очередь 
есть верное равенство.
То есть 
при 
и 
при 
.
Еще раз подчеркнем: БУДЬТЕ ВНИМАТЕЛЬНЫ С ОБЛАСТЬЮ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЮ ЗНАЧЕНИЙ!
Графики основных элементарных взаимно обратных функций.
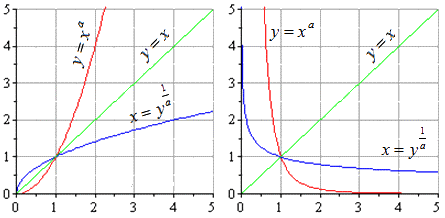
Взаимно обратные степенные функции, графики.
Для степенной функции 
при 
обратной является также степенная функция 
Если заменить буквы, то получим пару взаимно обратных функций и
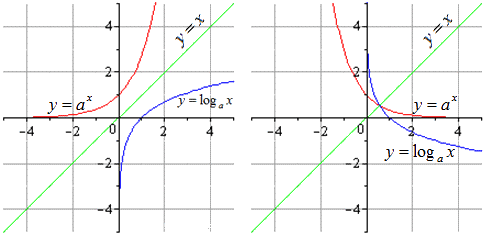
Взаимно обратные показательная и логарифмическая функции 
и 
, графики.
Подразумеваем, что а положительное и не равное единице число.
Графики для 
и для 
Взаимно обратные тригонометрические и обратные тригонометрические функции.
График главной ветви синуса и арксинуса (светлая область).
График главной ветви косинуса и арккосинуса (светлая область).
График главной ветви тангенса и арктангенса (светлая область).
График главной ветви котангенса и арккотангенса (светлая область).
Если Вам потребуются обратные функции для ветвей тригонометрических функций, отличных от главных, то соответствующую обратную тригонометрическую функцию нужно будет сдвинуть вдоль оси ординат на необходимое количество периодов.
Например, если Вам потребуется обратная функция для ветви тангенса на промежутке 
(эта ветвь получается из главной ветви сдвигом на величину 
вдоль оси ох ), то ей будет являться ветвь арктангенса, сдвинутая вдоль оси oy на .
Пока на этом закончим с обратными функциями.
Взаимно обратные функции
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
Алгоритм вывода формулы функции, обратной данной
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
Шаг 3. Ограничений на x и y нет
Шаг 3. Ограничений на x и y нет
Шаг 3. На исходную функцию накладываются ограничения
Шаг 3. На обратную функцию накладываются ограничения
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Графики пар взаимно обратных функций, найденных выше:
 |  |
 |  |
Примеры
Пример 1. Задайте формулой функцию, обратную данной.
Меняем аргумент и значение: x = 5y-4
Меняем аргумент и значение: x = 4y+1
$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$
Пример 2. Найдите функцию, обратную данной.
Постройте график исходной и обратной функции в одной системе координат.
$x = y^2 \Rightarrow y = \pm \sqrt
$x = y-3 \Rightarrow y = x+3$
$x = \frac<1>
$x = 1+ \sqrt
Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
1 комментарий
Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?