Объем что это геометрия
Объём (геометрия)
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Содержание
Подходы к определению
Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий, понятие объёма вводится аналогично понятию площади поверхности.
Понятие объёма допускает естественное обобщения до понятия 

Объёмы простейших тел
| Фигура | Формула | Обозначения |
|---|---|---|
| Куб |  |  — ребро куба — ребро куба |
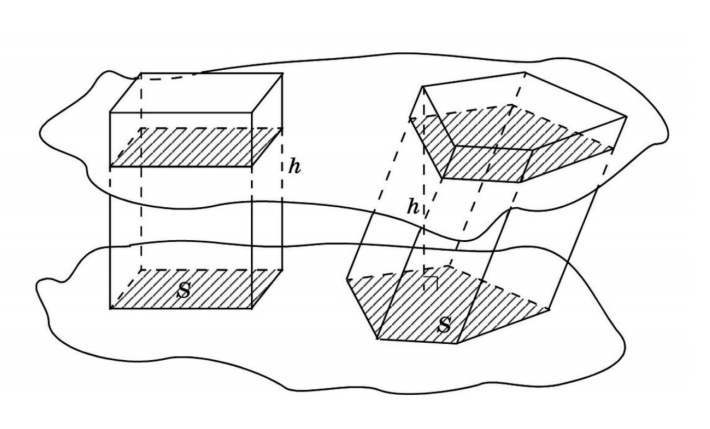
| Призма |  |  — площадь основания, — площадь основания,  — высота призмы — высота призмы |
| Цилиндр |  |  — радиус, — радиус,  — высота цилиндра — высота цилиндра |
| Шар |  |  — радиус — радиус |
| Эллипсоид |  |  — главные оси — главные оси |
| Пирамида |  |  — площадь основания, — площадь основания,  — высота пирамиды — высота пирамиды |
| Конус |  |  — радиус основания, — радиус основания,  — высота конуса — высота конуса |
Архимед сумел установить, что сфера и конусы с общей вершиной, вписанные в цилиндр, соотносятся следующим образом: два конуса : сфера : цилиндр как 1:2:3. Архимед просил выбить на своей могиле шар, вписанный в цилиндр. [1]
Интегральная формула
Объём тела в трехмерном пространстве вычисляется как определённый интеграл:

где 
Литература
Примечания
См. также
Ссылки
Полезное
Смотреть что такое «Объём (геометрия)» в других словарях:
Объём (значения) — Объём вообще величина, количество[1] Объём количественная характеристика пространства В математике: Объём (геометрия) Мера Жордана Мера Лебега Ориентированный объём Смешанный объём Объём торгов число акций, переходящее от продавцов к покупателям… … Википедия
Объём — У этого термина существуют и другие значения, см. Объём (значения). Объём Размерность L3 Единицы измерения СИ … Википедия
Геометрия — (от др. греч. γῆ Земля и μετρέω «мерю») раздел математики, изучающий пространственные структуры, отношения и их обобщения[1]. Содержание … Википедия
геометрия — и; ж. [греч. gē Земля и metreō измеряю]. Раздел математики, изучающий пространственные формы и отношения. // Учебный предмет, излагающий этот раздел математики. Урок геометрии. Преподаватель геометрии. // Разг. Учебник по этому предмету. * * *… … Энциклопедический словарь
Объём жёсткого диска — Динамика роста ёмкости жёстких дисков с 1980 года. Ось Y в логарифмическом масштабе, поэтому аппроксимирующая линия соответствует … Википедия
Геометрия — (гр. Земля измеряю) раздел математики, в котором изучаются пространственные отношения и формы и их обобщения. Возникновение геометрии обусловлено практическими потребностями измерения земельных участков, объёмов и др. Строгое построение геометрии … Концепции современного естествознания. Словарь основных терминов
Тело (геометрия) — У этого термина существуют и другие значения, см. Тело. Тело геометрическое «то, что имеет длину, ширину и глубину» в «Началах» Евклида, в учебниках элементарной геометрии ко всему «часть пространства, ограниченное своей образуемой формой» … Википедия
Объем (геометрия) — Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении трёхмерных тел трёхмерного евклидова пространства.… … Википедия
Формулы вычисления объема всех геометрических фигур
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Все формулы объема геометрических тел
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
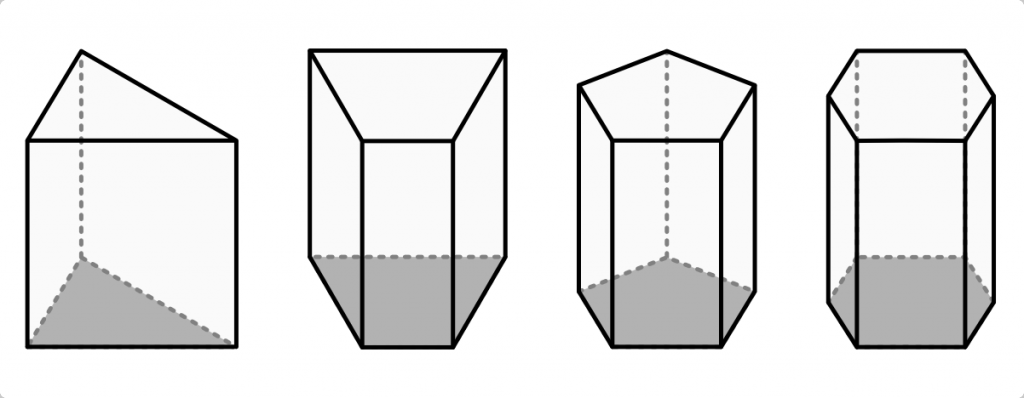
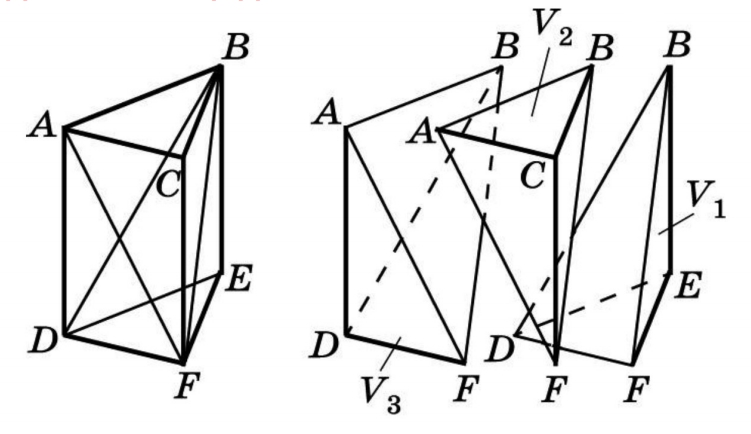
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
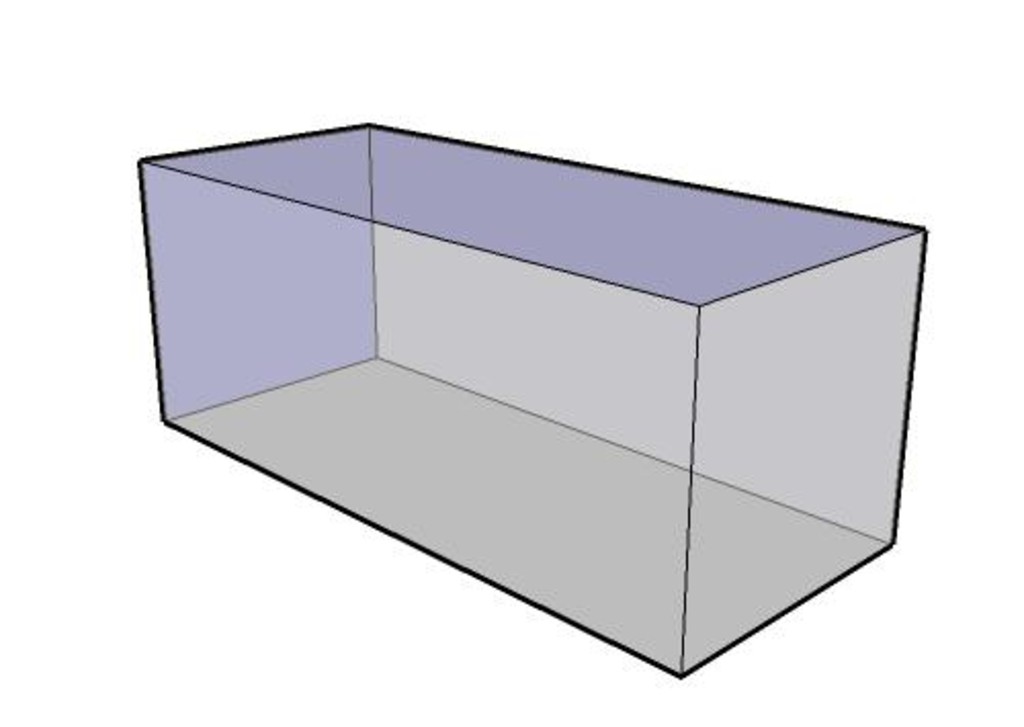
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
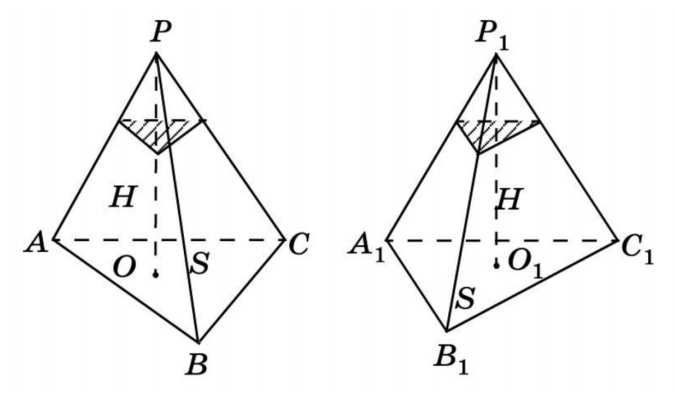
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
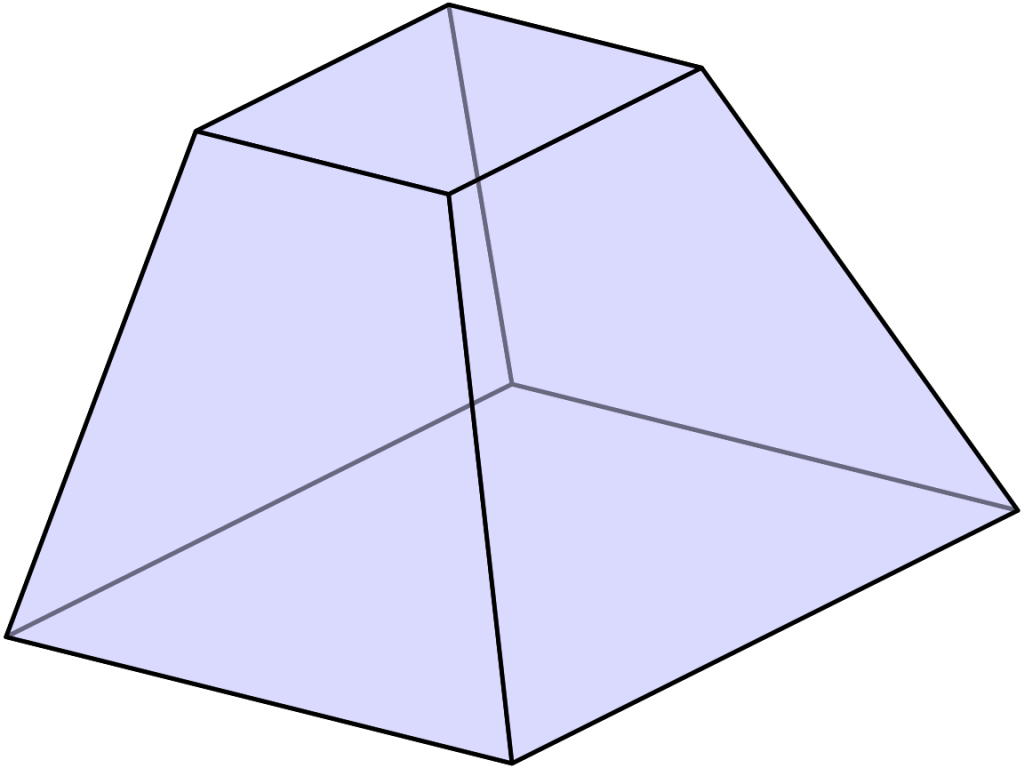
Объем усеченной пирамиды
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
Формула объема усеченной пирамиды:
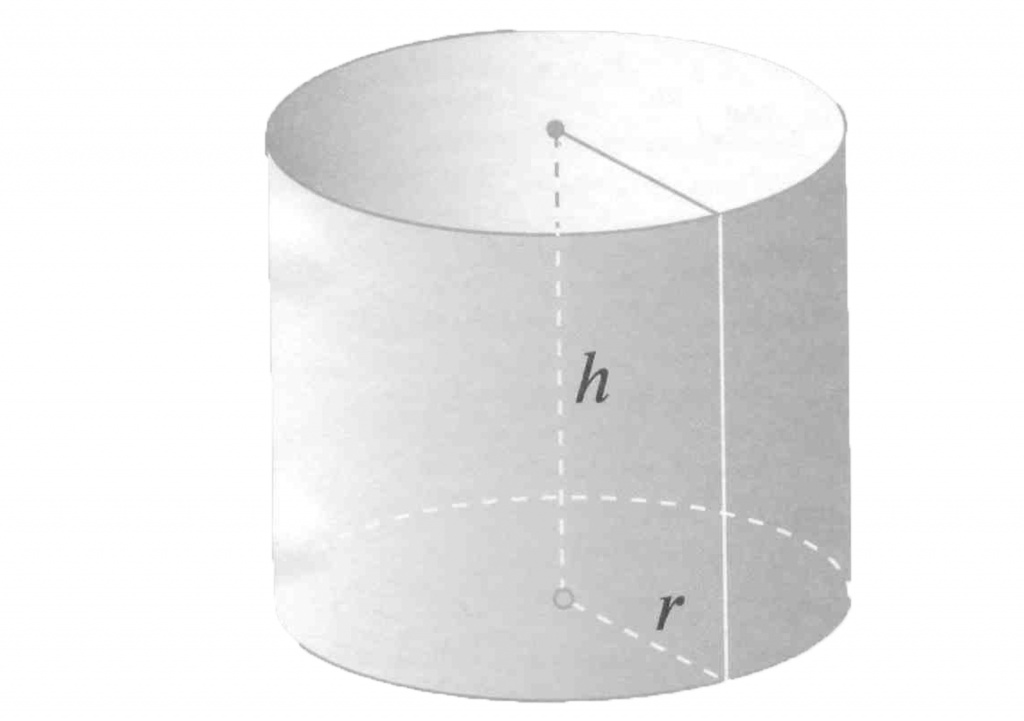
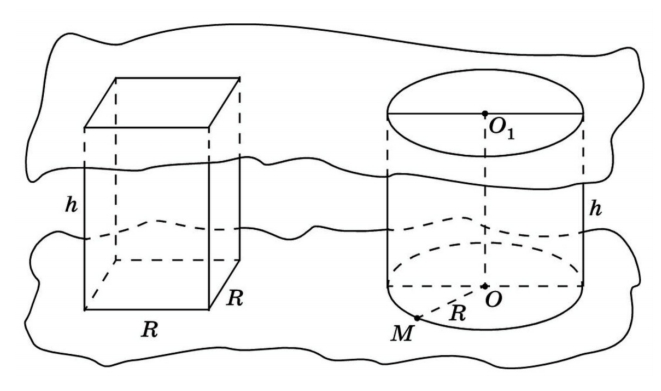
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
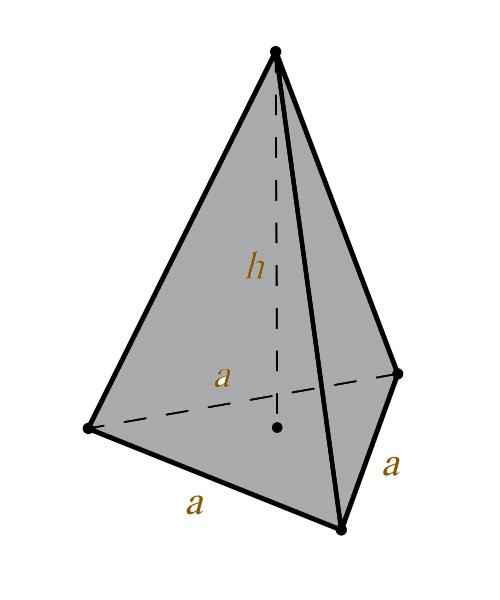
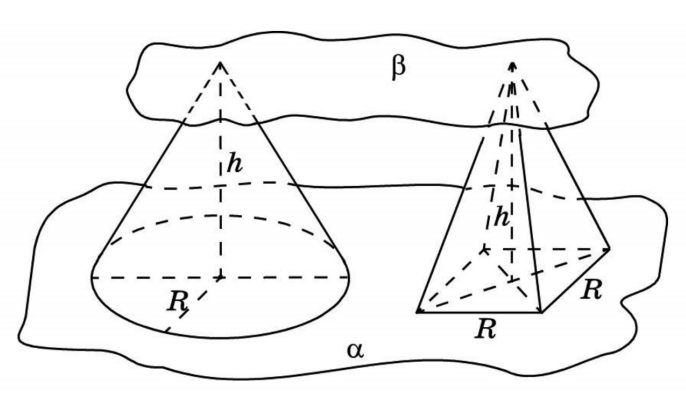
Объем правильной треугольной пирамиды
Формула объема правильной треугольной пирамиды:
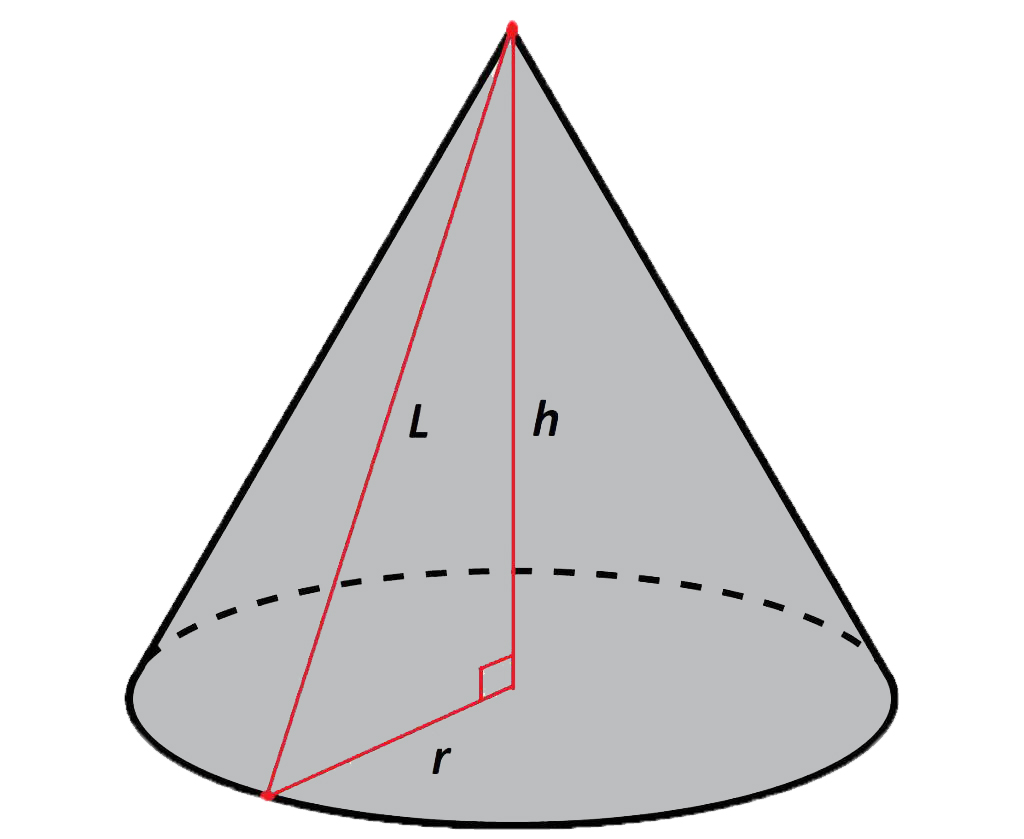
Объем конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H.
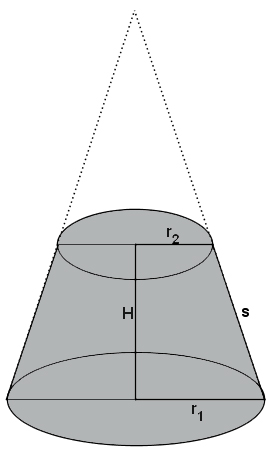
Объем усеченного конуса
Объем усеченного конуса равен разности объемов двух полных конусов.
Формула объема усеченного конуса:
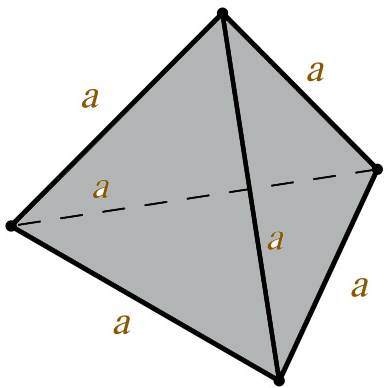
Объем тетраэдра
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
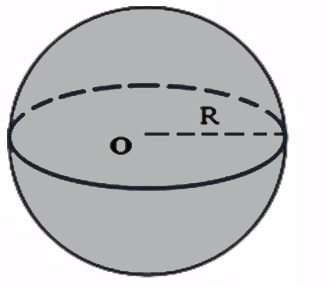
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.
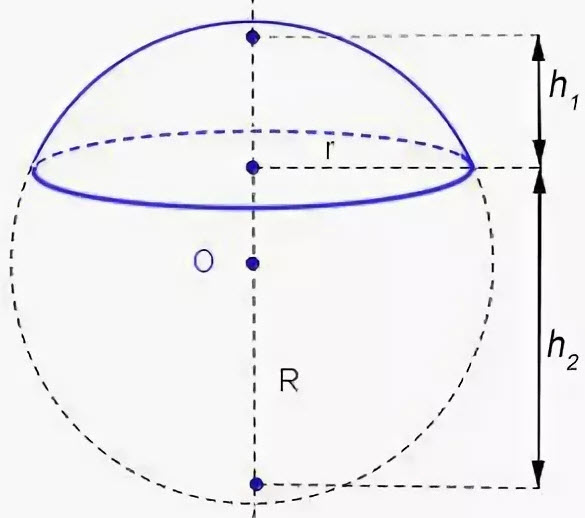
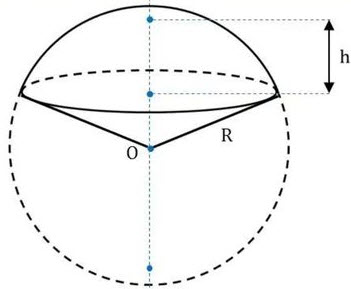
Объем шарового сегмента и сектора
Формула объема шарового сегмента:
Формула объема шарового сектора:
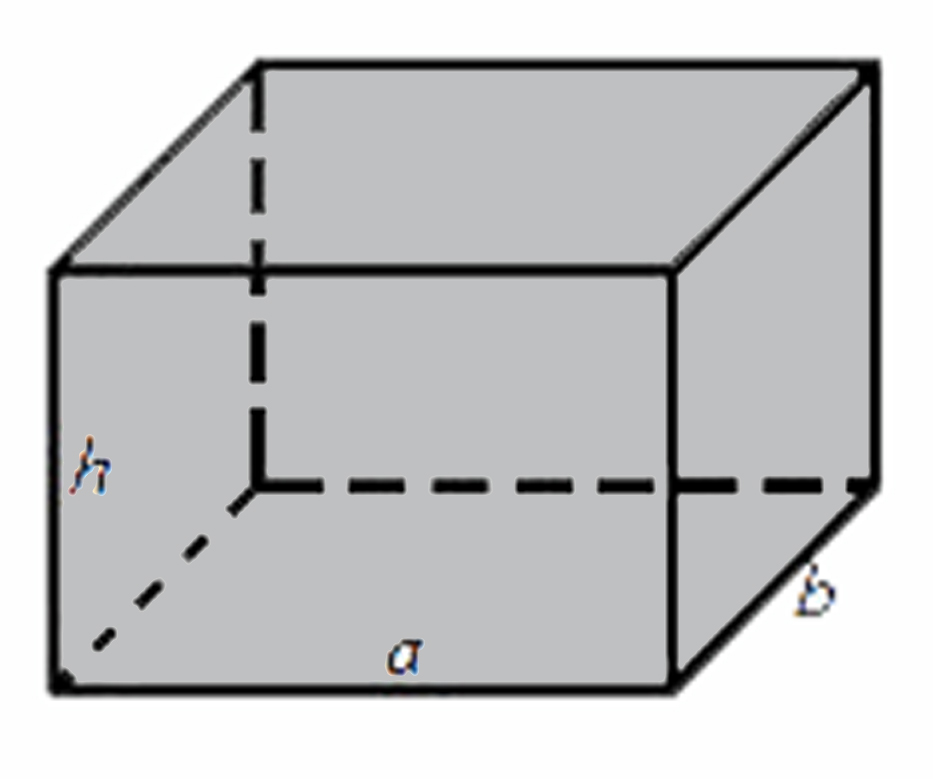
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
Формула объема.
Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.

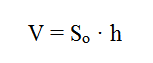
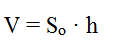

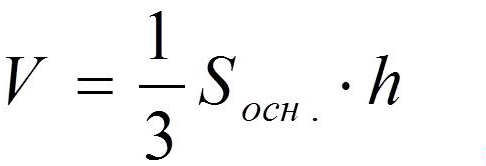
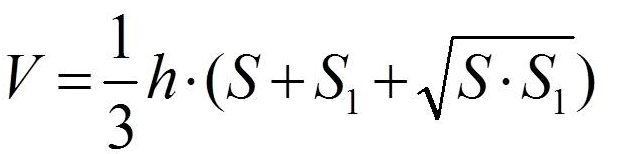
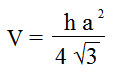

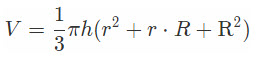
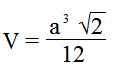
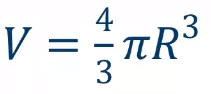
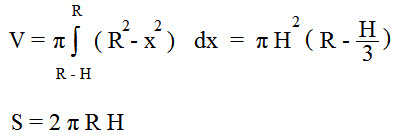
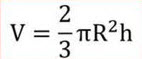
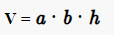















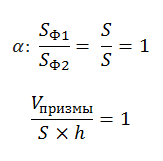








 №2.
№2.