О наличии мультиколлинеарности не свидетельствует факт того что близки к единице

ОТветы на синергию. Эконометрика. Автокорреляционная функция это функция от Тип ответа

Модель авторегрессии первого порядка

Обобщенный метод наименьших квадратов

Постоянство дисперсии случайного члена регрессионного уравнения

Отсутствие зависимости между остатками текущих и предыдущих наблюдений

Процесс не является стационарным в широком смысле

Показатель, характеризующий тесноту линейной стохастической связи между переменными

Явление линейной стохастической связи между переменными

Показатель, позволяющий установить факт наличия линейной

стохастической связи между переменными

Дисперсии зависимой переменной, объясняемую регрессией в общей ее дисперсии

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Статистической значимости модели в целом

Статической зависимости каждого из коэффициентов модели

Определения статической значимости каждого коэффициента уравнения

Наличие линейной зависимости между несколькими объясняющими переменными

Дисперсии коэффициентов регрессии

Числа структурных коэффициентов над числом приведенных

О мультиколлинеарности факторов

Значение коэффициента равно нулю

С ростом Х происходит убывание У

Объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной

Ранговое условие и порядковое условие со знаком равенства

Коэффициенты множественной детерминации некоторых объясняющих факторов с остальными

Переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии

Положительные и отрицательные

Эндогенных переменных минус единица

Отбор факторов, влияющих на результат и выбор вида уравнения

Парные и множественные

Необходимым и достаточным

Системы минус единица

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Проверки статистической значимости фактора

Можно рассматривать в узком и в широком смысле

Характеристика временного ряда, связанная с его стабильностью

Качество уровня регрессии в целом

По нормальному закону

Качество уравнения регрессии в целом

Ее математическое ожидание не равно ей

Связь между переменными, сложенная влиянием случайных факторов

Обладают свойством гетероскедастичности

Источник

Мультиколлинеарность

Последствия и признаки мультиколлинеарности

Признаки мультиколлинеарности

К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть разрешены?

Точных количественных критериев для обнаружения частичной мультиколлинеарности не существует. О наличии мультиколлинеарности может свидетельствовать близость к нулю определителя матрицы (X T X). Также исследуют значения парных коэффициентов корреляции. Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет.

С помощью какой меры невозможно избавиться от мультиколлинеарности?
a) увеличение объема выборки;
b) исключения переменных высококоррелированных с остальными;
c) изменение спецификации модели;
d) преобразование случайной составляющей.

Парные (линейные) и частные коэффициенты корреляции

Парный коэффициент корреляции изменяется в пределах от –1 до +1. Чем ближе он по абсолютной величине к единице, тем ближе статистическая зависимость между x и y к линейной функциональной. Положительное значение коэффициента свидетельствует о том, что связь между признаками прямая (с ростом x увеличивается значение y ), отрицательное значение – связь обратная (с ростом x значение y уменьшается).
Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции: если |r| 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.
Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются выборкой из некой генеральной совокупности, вычисленные по этим данным коэффициенты корреляции будут выборочными, т. е. они лишь оценивают связь. Необходима проверка значимости, которая отвечает на вопрос: случайны или нет полученные результаты расчетов.
Значимость парных коэффициентов корреляции проверяют по t-критерию Стьюдента. Выдвигается гипотеза о равенстве нулю генерального коэффициента корреляции: H₀: ρ = 0. Затем задаются параметры: уровень значимости α и число степеней свободы v = n-2. Используя эти параметры, по таблице критических точек распределения Стьюдента находят t_кр, а по имеющимся данным вычисляют наблюдаемое значение критерия:
, (2)
где r – парный коэффициент корреляции, рассчитанный по отобранным для исследования данным. Парный коэффициент корреляции считается значимым (гипотеза о равенстве коэффициента нулю отвергается) с доверительной вероятностью γ = 1- α, если t_Набл по модулю будет больше, чем t_крит.
Если переменные коррелируют друг с другом, то на значении коэффициента корреляции частично сказывается влияние других переменных.

Пошаговая регрессия

На втором шаге строится уравнение регрессии с одной переменной, имеющей максимальный по абсолютной величине парный коэффициент корреляции с результативным признаком.

На третьем шаге в модель вводится новая переменная, имеющая наибольшее по абсолютной величине значение частного коэффициента корреляции с зависимой переменной при фиксированном влиянии ранее введенной переменной.
При введении в модель дополнительного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, т. е. коэффициент множественной детерминации увеличивается незначительно, то ввод нового фактора признается нецелесообразным.

Источник

Как выявить мультиколлинеарность

Вы будете перенаправлены на Автор24

Понятие мультиколлинеарности

Мультиколлинеарность – это наличие зависимости между линейными объясняющими факторами.

По сути, это регрессионный анализ, представляющий собой метод статистического анализа одной или более величин, оказывающих влияние на другую величину. Влияние оказывают независимые переменные или предикторы, а под влияние попадают критериальные или зависимые переменные. Стоит отметить, что регрессионная зависимость показывает только математическую взаимосвязь величин, но не описывает ее причину и следствие.

Регрессионный анализ применяется для оценки степени устойчивости связи между независимыми и зависимыми переменными, позволяет измерить зависимую величину через независимую, а также оценить степень влияния одних величин на изменчивость других.

Мультиколлинеарность бывает двух видов:

Коллинеарность полного типа всегда приводит к неопределенности всех рассматриваемых величин. То есть, внесение дополнительных коэффициентов все равно приведет к формированию того же результата, что и без их использования. Такую модель сложно идентифицировать, так как в ней уже присутствует неопределенность. Именно поэтому, проблему коллинеарности полного типа решают еще на этапе подбора рассматриваемых параметров. То есть, неточный результат будет связан с неправильным подбором изначальных переменных. Однако, сильная зависимость между факторами неизбежна.

Совершенная и несовершенная мультиколлинеарность

Проблемы возникают тогда, когда мультиколлинеарность возникает при множественной регрессии. В этом случае она становится совершенной, так как имеет бесконечное множество решений. Конечные коэффициенты зависимости параметров друг от друга определить становится невозможным. Совершенная мультиколлинеарность – это идеальная модель, в которой невозможно выявить влияние тех или иных факторов на конечный результат. Для совершенной мультиколлинеарности характерна строгая функциональная связь.

Готовые работы на аналогичную тему

В практических примерах чаще всего встречается несовершенная мультиколлинеарность, которая проявляется в очень тесной связи между переменными. Коэффициент связи имеет очень большие значения между рассматриваемыми переменными. Если его значение близко к единице, то говорят о почти совершенной мультиколлинеарности. Явление мультиколлинеарности говорит о том, что в модели очень сложно разделить степень влияния отдельных факторов на исследуемую переменную. Этот вывод хорошо демонстрирует диаграмма Венна:

Рисунок 1. Диаграмма Венна. Автор24 — интернет-биржа студенческих работ

Выявление мультиколлинеарности сказывается на точности исследуемой модели. Метод наименьших квадратов дает достаточно высокие показатели несмещенности линейной зависимости, даже при незначительной величине статистических коэффициентов. Но несмещенность свидетельствует о том, что необходимо проводить многократные исследования, которые будут перемещать величины к их истинным значениям. Такой подход при изучении экономических зависимостей неэффективен, так как хозяйственные связи динамичны. Наличие мультиколлинеарности ведет к следующим последствиям:

Таким образом, мультиколлинеарность говорит исследователю о том, что параметр подвергается влиянию факторов, но вычленить степень их отдельного влияния на него практически невозможно.

Признаки мультиколлинеарности

Выявление мультиколлинеарности происходит по следующим признакам:

Еще одним методом определения мультиколлинеарности можно назвать наличие линейной объясняющей переменной, которая объясняет другие переменные.

Источник

4.1. Мультиколлинеарность

Выделяют два вида мультиколлинеарности:

Под строгой мультиколлинеарностью понимается ситуация, когда между регрессорами в модели есть точная линейная связь, т.е. когда одна объясняющая переменная точным образом линейно выражается через другие.

Представим, например, что при анализе макроэкономической модели в качестве переменных в неё включили экспорт, импорт и чистый экспорт. Чистый экспорт равен разности между экспортом и импортом и, следовательно, при включении в модель этих трёх переменных окажется, что регрессоры модели линейно выражаются друг через друга.

В терминах матричной записи точная мультиколлинеарность предполагает линейную зависимость столбцов матрицы регрессоров, откуда следует неполный ранг матрицы регрессоров. Это означает, что при полной мультиколлинеарности невозможно вычислить МНК-оценки коэффициентов, потому что матрица является вырожденной, и матрица не определена.

Из определения и из приведенного выше примера легко догадаться, как можно решить проблему строгой мультиколлинеарности. Для этого следует исключить лишнюю переменную. Например, если в модели уже учтены экспорт и импорт, то понятно, что включение ещё и чистого экспорта не принесет никакой дополнительной информации, и этой третьей переменной можно безболезненно пожертвовать.

Современные эконометрические пакеты при возникновении чистой мультиколлинеарности сами избавляются от одной из линейно зависимых переменных, чтобы вычисление МНК-оценок стало технически возможным.

Частичная мультиколлинеарность — это ситуация, когда между объясняющими переменными нет точной линейной связи, но эти переменные сильно коррелируют между собой. Иными словами, они не линейно зависимы, но «почти» линейно зависимы. При частичной мультиколлинеарности вычислить МНК-оценки можно, однако стандартные ошибки оценок коэффициентов оказываются высокими, а точность оценок коэффициентов — низкой. Так происходит потому, что при сильной корреляции двух регрессоров в выборке они, как правило, меняются одновременно, и оказывается трудно отличить влияние одного регрессора на зависимую переменную от влияния другого. Таким образом, основным негативным последствием мультиколлинеарности является снижение точности оценки отдельных коэффициентов.

Частичная мультиколлинеарность не нарушает ни одну из предпосылок классической линейной модели множественной регрессии и поэтому не приводит к смещению оценок коэффициентов модели.

Это особенно хорошая новость потому, что на практике почти в любой множественной регрессии объясняющие переменные в той или иной степени коррелированы. Поэтому частичная мультиколлинеарность в данных наблюдается очень часто. Представьте, например, что вы моделируете выпуск фирмы некоторой отрасли в зависимости от количества используемых фирмой труда и физического капитала (то есть, как сказали бы экономисты, моделируете производственную функцию). Скорее всего, в вашей выборке будут большие фирмы и маленькие, причем большие фирмы в среднем будут использовать относительно много каждого из факторов производства, а маленькие, напротив, относительно мало. В результате переменные, характеризующие количество труда и количество капитала, будут положительно коррелированы друг с другом.

Есть несколько способов выявить мультиколлинеарность на этапе предварительного анализа данных (то есть ещё до оценки параметров уравнения регрессии). О наличии существенной частичной мультиколлинеарности в модели говорят:

где — это коэффициент детерминации из оцененной вспомогательной регрессии.

Если коэффициенты VIF для всех регрессоров оказались меньше 10, это значит, что существенной мультиколлинеарности в модели не наблюдается. В противном случае стоит сделать вывод о том, что в модели есть мультиколлинеарность.

Пример 4.1. Мультиколлинеарность.

Эконометрист исследует модель:

На этапе предварительного анализа данных он оценил следующие вспомогательные уравнения:

Что можно сказать о наличии мультиколлинеарности в исходной модели?

Решение:

Некоторые признаки мультиколлинеарности можно увидеть уже после оценки параметров модели. Перечислим их:

— Неустойчивость результатов. Небольшое изменение исходных данных приводит к существенному изменению оценок коэффициентов. Например, если после оценки уравнения по 200 наблюдениям вы исключили из выборки несколько точек, оценили модель заново и обнаружили сильное изменение результатов.

— Неправдоподобность результатов. Оценки коэффициентов имеют неправильные с точки зрения экономической теории знаки или неоправданно большие значения. Стоит отметить, что причиной возникновения такой ситуации может быть не только потеря точности оценивания из-за мультиколлинеарности, но и гораздо более серьезные проблемы, например, смещение из-за пропуска существенной переменной (не говоря уж о том, что не все экономические теории прошлого проходят испытание современными данными).

Что можно предпринять, если вы столкнулись с негативными последствиями мультиколлинеарности в вашей модели? Существует несколько путей решения этой проблемы.

Если есть возможность увеличить количество наблюдений, то это отличный вариант, так как больший размер выборки увеличит точность результатов, компенсировав её потерю из-за мультиколлинеарности.

Мультиколлинеарность будет устранена, если вы исключите из уравнения тот регрессор, который сильно коррелирован с остальными объясняющими переменными модели. Однако следует помнить, что применение этого способа не всегда целесообразно, так как может привести к гораздо более серьезным последствиям: смещению оценок в результате пропуска существенной переменной. Скажем, в нашем примере про производственную функцию ни труд, ни капитал из уравнения исключать не хотелось бы, так как ясно, что выпуск фирмы зависит от каждого из этих факторов производства.

Решением проблемы может быть использование вместо отдельных переменных их линейных комбинаций. Возвращаясь к нашему примеру с экспортом и импортом, заметим, что эти переменные, включенные в модель по отдельности, могут быть причиной мультиколлинеарности, так как обычно коррелированы друг с другом. Однако, заменив их чистым экспортом (который как раз и представляет собой их линейную комбинацию), вы сможете избежать этой проблемы. Другой пример: представим, что вы оцениваете зависимость успеваемости студента физического факультета от баллов за ЕГЭ по математике и по физике, которые этот студент получил, будучи школьником. Так как два этих регрессора наверняка коррелированы, то вместо включения в модель каждого из них по отдельности вы могли бы оставить в уравнении одну переменную — средний балл ЕГЭ по двум этим предметам.

Использование альтернативных (нелинейных) форм зависимостей в некоторых случаях также может снизить остроту проблемы мультиколлинеарности. Оценивание такого рода моделей мы обсудим в конце данной главы.

Некоторые специфические инструменты, которые иногда тоже могут быть полезны в борьбе с мультиколлинеарностью, обсуждаются в рамках курсов машинного обучения и многомерного статистического анализа. См.: метод главных компонент, LASSO и ridge-регрессии, метод эластичной сети.↩︎

Источник

Мультиколлинеарность

Коэффициенты интеркорреляции (т. е. сила связи между объясняющими переменными) позволяют исключить из модели регрессии дублирующие факторы. Две переменных явно коллинеарны, когда они находятся между собой в линейной зависимости, если коэффициент корреляции > 0,7.

Поскольку одним из условий нахождения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы модели коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение в эконометрике отдается не фактору, более сильно связанному с результатом, а фактору, который при сильной связи с результатом имеет наименьшую тесноту связи с другими факторами. Т.е. коэффициент корреляции между факторами меньше 0,3 или, в идеале, близок к нулю. В этом условии проявляется специфика множественной регрессии как метода исследования комплексного влияния факторов на результат в условиях их независимости друг от друга.

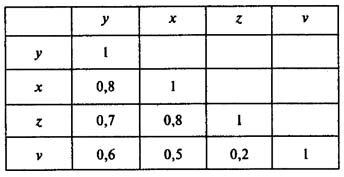
Матрица парных коэффициентов корреляции

Пусть, например, при изучении зависимости у = f(x, z, v) матрица парных коэффициентов корреляции оказалась следующей:

Факторы х и z дублируют друг друга, т.к. связь между ними сильная (больше 0,7). В анализ нужно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция фактора х с у, но значительно слабее межфакторная связь Rzv

Источник