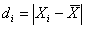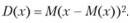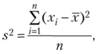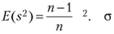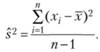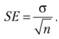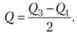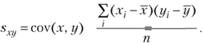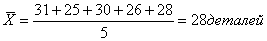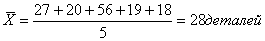О чем свидетельствует высокая дисперсия текущих оценок
О чем свидетельствует высокая дисперсия текущих оценок
Нормативно-ориентированный тест должен хорошо дифференцировать испытуемых. Это означает, что индивидуальные тестовые баллы должны в достаточной степени отличаться друг от друга.
Вариацию тестовых результатов задают отклонения от среднего значения
Для удобства вычисления, преобразуем выражение для дисперсии.
Используя полученное выражение, перепишем формулу для дисперсии
Подставим численные значения
Таким образом, дисперсия тестовых баллов в нашем примере равна 4.9. Подобные расчеты удобно проводить с использованием табличного процессора Microsoft Excel, входящего в стандартный офисный пакет. Для этого необходимо использовать статистическую функцию «ДИСП», для которой надо указать диапазон ячеек со значениями индивидуальных баллов испытуемых.
Величина дисперсии тестовых баллов позволяет судить о качестве теста, о его дифференцирующей способности. Малая величина дисперсии говорит о том, что тест плохо различает испытуемых по уровню знаний, не позволяет с приемлемой точностью ранжировать их. Слишком большая дисперсия указывает на сильную неоднородность группы испытуемых, на возможные нарушения процедуры тестирования, на недостаточно ясные формулировки заданий и т.п. В случае оптимальной величины дисперсии, распределение тестовых баллов близко к нормальному.
М.Б.Челышкова 7 считает, что если среднее арифметическое примерно равно утроенному стандартному отклонению,
то можно считать дисперсию оптимальной, а распределение тестовых баллов близким к нормальному.
Отметим, что это утверждение справедливо не для всех случаев. Возможны ситуации, когда среднее арифметическое гораздо больше утроенного стандартного отклонения, но распределение тестовых баллов, тем не менее, достаточно близко к нормальному.
Рассмотрим следующий модельный пример. Пусть в результате тестирования мы получили следующую таблицу частот.
Русские Блоги
Что такое высокая / низкая дисперсия, высокое / низкое отклонение (рекомендуемое чтение)
Концепция
Отклонение:Описывает разницу между ожидаемым значением (оценочным значением) и истинным значением. Чем больше отклонение, тем больше отклонение от реального набора данных.
(PS: если предположить, что яблочко является наиболее подходящей моделью для данных, чем дальше от яблочка, тем хуже будет наш прогноз)
Разница:Описывает диапазон изменения прогнозируемого значения, степень дисперсии, то есть расстояние от его ожидаемого значения. Чем больше дисперсия, тем больше разбросано распределение данных прогноза.
Ошибка на основе дисперсии:Ошибки на основе дисперсии описывают изменчивость предсказаний модели для заданных данных. Например, когда вы повторяете процесс построения полной модели несколько раз, разница заключается в том, насколько сильно она изменяется между различными отношениями в модели прогнозирования.
Далее мы объединяем четыре картинки:
Объяснение:
Вверху слева: низкое отклонение, низкая дисперсия. Результатом является то, что точность результатов прогнозирования очень высока, а модель относительно устойчива (стабильна), а результаты прогнозирования являются высоко концентрированными.
Вверху справа: низкое отклонение, высокая дисперсия. Результатом является то, что точность результатов прогнозирования высока, а модель нестабильна, а результаты прогнозирования более расходятся.
Внизу слева: высокое отклонение, низкая дисперсия. Результатом является то, что точность результатов прогнозирования низкая, но модель стабильна, а результаты прогнозирования относительно концентрированы.
Внизу справа: высокое отклонение, высокая дисперсия. Результатом является то, что точность результатов прогнозирования низкая, модель нестабильна, а результаты прогнозирования более расходятся.
Позвольте привести пример
Представьте, что вы управляли вертолетом Black Hawk и получили приказ атаковать вражеские силы на земле. Затем вы нажали десятки шаттлов. Результаты таковы:
1. Пули в основном попадают в дерево, проходящее мимо команды, и даже люди, ожидающие кролика рядом с деревом, остаются невредимыми. Это означает, что дисперсия мала (пули очень концентрированные), а отклонение велико (очень далеко от цели). далеко).
2. Пуля попала в дерево, камень, кролик и другие люди рядом с деревом, также были расстреляны цветы и трава, но враг был в целости и сохранности, это большая разница (пуля повсюду), отклонение велико (далеко от цели далеко).
4. Одна пуля не тратится впустую, каждая убивает вражескую армию, как Восьмая армия в антияпонской военной драме, это то, что дисперсия мала (пули сконцентрированы в одной позиции), а отклонение мало (позиция, где пули сконцентрированы, точно Где это должно быть расстреляно).
Дисперсия описывает степень дисперсии данных, которая считается «без присмотра», объективный показатель, отклонение, и описывает, как далеко данные находятся от центра, который мы ожидаем. Они «контролируются» и являются индикатором участия людей в знаниях.
Трижды понять
Offset (смещение): Объект представляет собой единую модель, Разница между ожидаемым результатом и реальной оценкой.
Разница (Дисперсия): Объект представляет собой несколько моделей, указывающих степень различия между несколькими моделями.
Возьмите приведенную выше картинку в качестве примера:
1. Отклонение модели в верхнем левом углу является наибольшим, а отклонение модели в нижнем правом углу наименьшим;
2. Модельная дисперсия в верхнем левом углу самая маленькая, а модельная дисперсия в нижнем правом углу самая большая
В целом связь между отклонением, дисперсией и сложностью модели показана на следующем рисунке:
На практике нам нужно найти точку, где отклонение и дисперсия малы. Из приведенного выше рисунка видно, что суммарная ошибка наименьшая в точке, где отклонение и дисперсия малы.
В XGBOOST мы выбираем как можно больше деревьев, насколько это возможно, чтобы уменьшить отклонение модели;
Благодаря перекрестной проверке, проверке набора проверок и регуляризации дисперсия модели уменьшается, чтобы получить меньшую ошибку обобщения.
расширять
Разверните приведенную выше формулу, а затем используйте отклонение и дисперсию для выражения:
Из вышеприведенной формулы также видно, что для того, чтобы сделать ошибку низкой, необходимо сделать отклонение и дисперсию низкими.
Дисперсия и ее оценка
Определение дисперсии случайных величин
Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.
В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:
где М(х) – математическое ожидание, а D(х) – дисперсия.
На основе данной формулы можно вывести другую, которая дает оценку дисперсии:
В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.
Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:
Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:
Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.
Характеристика оценивания стандартного отклонения
Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:
где SE – стандартная ошибка.
Данная статистика необходима для интервальной оценки исследуемой случайной величины.
Характеристика оценки полумежквартильного интервала
Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.
Квартиль – это вариант названия квантиля распределения.
При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:
Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.
Характеристика ковариации
Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:
Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.
О чем свидетельствует высокая дисперсия текущих оценок
— область применения и методику расчёта степенных средних величин;
— исчислять степенные средние величины;
— формулировать вывод по полученным результатам.
Наряду со средними величинами в статистике исчисляются показатели вариации. Вариацией в статистике называются различия индивидуальных значений изучаемого признака. Возникает вариация в силу того, что отдельные значения признака статистической совокупности формируются под воздействием разнообразных факторов. Значение изучения вариации в том, что по колеблемости признаков можно судить о качественной однородности совокупности. Совокупности могут иметь одинаковые значения средней величины, но отличаться колеблемостью индивидуальных значений.
Например : По имеющимся данным о дневной выработке рабочих двух бригад определить среднюю выработку рабочего за день в каждой бригаде, сделать вывод об однородности рассматриваемых совокупностей и надёжности их средних.
Выработка в первой бригаде: 31, 25, 30, 26, 28 деталей.
Выработка во второй бригаде: 27, 20, 56, 19, 18 деталей.
Исходные данные не сгруппированы, поэтому для расчёта средней выработки применяем среднюю арифметическую простую. Средняя дневная выработка рабочего:
в первой бригаде 
во второй бригаде 
Среднедневная выработка рабочего в обеих бригадах одинакова, но индивидуальные значения выработки во второй бригаде подвержены значительным колебаниям. Это вызывает необходимость измерять вариацию.
К абсолютным показателям вариации относятся
размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
В нашем примере размах вариации индивидуальной выработки:
в первой бригаде R1 =31-25=6 деталей
во второй бригаде R2 =56-18=38 деталей
Сравнение этих показателей свидетельствует о том, что размах вариации индивидуальной выработки во второй бригаде на 32 детали больше, чем в первой бригаде. Однако размах вариации не улавливает колеблемости вариантов внутри изучаемой совокупности. Для получения обобщающей характеристики колеблемости всех вариантов совокупности исчисляются другие показатели вариации.
Среднее линейное отклонение даёт обобщённую характеристику степени колеблемости признака в совокупности относительно среднего уровня признака и рассчитывается как средняя арифметическая из индивидуальных линейных отклонений по формуле:
— для невзвешенных данных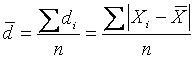 
— для взвешенных данных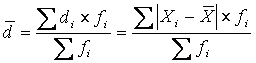 
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируют состав работающих, ритмичность производства, равномерность поставок материалов; разрабатывают системы материального стимулирования. Но этот показатель усложняет расчёты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
В статистике дисперсия, центральный момент второго порядка, является оценкой одноимённого показателя теории вероятностей и оценкой дисперсии в математической статистике, что позволяет использовать теоретические положения этих дисциплин для анализа социально – экономических процессов. На дисперсии практически основаны все метод математической статистики. Большое значение имеет правило сложения дисперсий. Дисперсия рассчитывается как средний квадрат отклонений индивидуальных значений признака от среднего
значения признака по формуле:
— для невзвешенных данных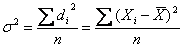 
— для взвешенных данных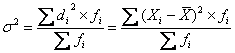 
Для расчёта показателей вариации в нашем примере строим вспомогательную таблицу:
Индивидуальное линейное отклонение 