О чем свидетельствует информация об увеличении коэффициента джинни в какой либо стране
Коэффициент Джини по странам или индекс концентрации доходов во всем мире
Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по какому-либо изучаемому признаку.
Коротко о том, что такое “Коэффициент Джини”:
Коэффициент Джини (индекс концентрации доходов) — статистический показатель для оценки экономического равенства. Его придумал экономист Джини Коррадо. Он показывает равномерность распределения дохода или богатства между членами общества.
Для тех, кто хочет узнать об этом подробнее:
Коэффициент Джини 26
Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по какому-либо изучаемому признаку. Используется для оценки экономического неравенства. Коэффициент Джини изменяется от 0 до 1. Чем больше его значение отклоняется от нуля и приближается к единице, тем в большей степени доходы сконцентрированы в руках отдельных групп населения. Индекс Джини — процентное представление этого коэффициента. Наиболее часто в современных экономических расчётах в качес.
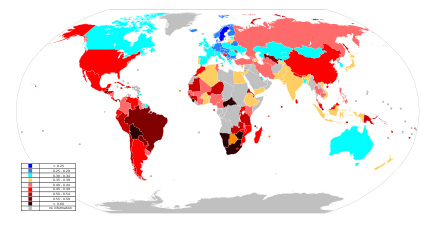
Карта с коэффициентом Джини по странам во всем мире за 2019 год
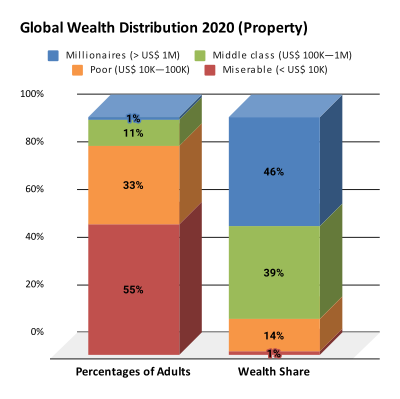
Простыми словами, данный коэффициент показывает неравенство богатств во всем мире. Согласно карте в России, США, Швеции и Нидерландах самый высокий коэффициент Джини. Это 4 страны-лидера, где все богатства (финансовые, экономические и тд.) максимально сконцентрированы в руках отдельных групп населения.
Коэффициент Джини измеряет неравенство между значениями частотного распределения (например, уровнями дохода ). Нулевой коэффициент Джини выражает полное равенство, когда все значения одинаковы (например, когда у всех одинаковый доход). Коэффициент Джини, равный единице (или 100%), выражает максимальное неравенство между ценностями (например, для большого количества людей, когда только один человек имеет весь доход или потребление, а все остальные не имеют ничего, коэффициент Джини будет почти равным единице).
Есть некоторые проблемы с интерпретацией коэффициента Джини. Одно и то же значение может быть результатом множества разных кривых распределения. Следует учитывать демографическую структуру. В странах со стареющим населением или с бэби-бумом коэффициент Джини до вычета налогов растет, даже если реальное распределение доходов работающих взрослых остается неизменным. Ученые разработали более десятка вариантов коэффициента Джини.
СОДЕРЖАНИЕ
История
Определение
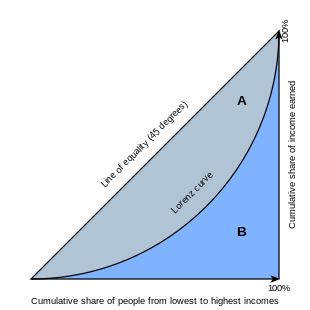
Графическое представление коэффициента Джини
С точки зрения упорядоченных по доходу процентилей населения, коэффициент Джини представляет собой совокупный дефицит от равной доли общего дохода до каждого процентиля. Затем этот суммарный дефицит делится на значение, которое оно имело бы в случае полного равенства.
Если все люди имеют неотрицательный доход (или богатство, в зависимости от обстоятельств), коэффициент Джини теоретически может варьироваться от 0 (полное равенство) до 1 (полное неравенство); иногда его выражают в процентах от 0 до 100. В действительности оба крайних значения не достигаются. Если возможны отрицательные значения (например, отрицательное богатство людей с долгами), то коэффициент Джини теоретически может быть больше 1. Обычно среднее (или общее) считается положительным, что исключает коэффициент Джини меньше нуля.
Когда распределение дохода (или богатства) задано как непрерывная функция распределения вероятностей p ( x ), коэффициент Джини снова составляет половину относительной средней абсолютной разницы:
Расчет
Хотя распределение доходов в любой конкретной стране не всегда соответствует теоретическим моделям в действительности, эти функции дают качественное понимание распределения доходов в стране с учетом коэффициента Джини.
Пример: два уровня дохода
Пресловутый случай, когда самые богатые 20% имеют 80% всего дохода (см. Принцип Парето ), приведет к коэффициенту Джини дохода не менее 60%.
Часто упоминаемый случай, когда 1% всего населения мира владеет 50% всего богатства, означает, что коэффициент Джини богатства составляет не менее 49%.
Альтернативные выражения
Дискретное распределение вероятностей
Непрерывное распределение вероятностей
тогда кривая Лоренца L ( F ) может быть представлена как функция, параметрическая в L ( x ) и F ( x ), а значение B может быть найдено интегрированием :
Коэффициент Джини также можно рассчитать непосредственно из кумулятивной функции распределения F ( y ). Определив μ как среднее значение распределения и указав, что F ( y ) равно нулю для всех отрицательных значений, коэффициент Джини определяется как:
Коэффициент Джини может быть выражен через функцию квантиля Q ( F ) (обратная кумулятивной функции распределения: Q ( F ( x )) = x )
Другие подходы
Если кривая Лоренца аппроксимируется на каждом интервале как линия между последовательными точками, то область B может быть аппроксимирована трапециями и:
является результирующим приближением для G. Более точные результаты могут быть получены с использованием других методов аппроксимации площади B, таких как аппроксимация кривой Лоренца квадратичной функцией по парам интервалов или построение подходящей гладкой аппроксимации базовой функции распределения, которая соответствует известные данные. Если также известны среднее значение генеральной совокупности и граничные значения для каждого интервала, их также можно часто использовать для повышения точности приближения.
Таким образом, G можно выразить как функцию взвешенной оценки по методу наименьших квадратов константы A, и это можно использовать для ускорения вычисления оценки складного ножа для стандартной ошибки. Экономист Дэвид Джайлз утверждал, что стандартную ошибку оценки A можно использовать для получения ошибки оценки G напрямую, вообще без использования складного ножа. Этот метод требует только использования обычной регрессии наименьших квадратов после упорядочивания выборочных данных. Результаты выгодно сравниваются с оценками, полученными с помощью складного ножа, с улучшением согласия с увеличением размера выборки.
Однако с тех пор утверждалось, что это зависит от предположений модели о распределении ошибок и независимости членов ошибок, предположений, которые часто не действительны для реальных наборов данных. Эта тема все еще обсуждается.
Гильермина Жассо и Ангус Дитон независимо предложили следующую формулу для коэффициента Джини:
ФАО объясняет другую версию формулы.
Обобщенные индексы неравенства
где p j взвешивает единицы по их доле в населении, а f ( r j ) является функцией отклонения r j каждой единицы от 1, точки равенства. Смысл этого обобщенного индекса неравенства заключается в том, что индексы неравенства различаются, потому что они используют разные функции расстояния между коэффициентами неравенства ( r j ) от 1.
Распределения доходов
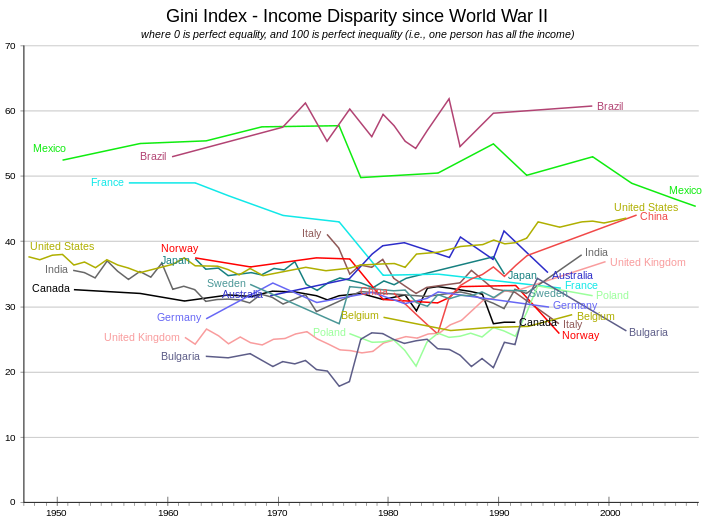
Коэффициент Джини для всего мира оценивается различными сторонами в диапазоне от 0,61 до 0,68. На графике показаны значения, выраженные в процентах от их исторического развития для ряда стран.
Индексы Джини регионального дохода
Индекс Джини мирового дохода с 1800-х годов
В таблице ниже представлены расчетные коэффициенты Джини мирового дохода за последние 200 лет, рассчитанные Милановичем.
| Год | Мировые коэффициенты Джини |
|---|---|
| 1820 г. | 0,43 |
| 1850 г. | 0,53 |
| 1870 г. | 0,56 |
| 1913 г. | 0,61 |
| 1929 г. | 0,62 |
| 1950 | 0,64 |
| 1960 г. | 0,64 |
| 1980 г. | 0,66 |
| 2002 г. | 0,71 |
| 2005 г. | 0,68 |
Более подробные данные из аналогичных источников показывают непрерывное снижение с 1988 года. Это объясняется глобализацией, увеличивающей доходы миллиардов бедных людей, в основном в таких странах, как Китай и Индия. Развивающиеся страны, такие как Бразилия, также улучшили базовые услуги, такие как здравоохранение, образование и санитария; другие, такие как Чили и Мексика, приняли более прогрессивную налоговую политику.
| Год | Мировые коэффициенты Джини |
|---|---|
| 1988 г. | 0,80 |
| 1993 г. | 0,76 |
| 1998 г. | 0,74 |
| 2003 г. | 0,72 |
| 2008 г. | 0,70 |
| 2013 | 0,65 |
Страны по индексу Джини
Социального развития
Коэффициент Джини широко используется в таких разнообразных областях, как социология, экономика, здравоохранение, экология, инженерия и сельское хозяйство. Например, в социальных науках и экономике, помимо коэффициентов Джини дохода, ученые опубликовали коэффициенты Джини образования и коэффициенты Джини возможностей.
Образование
Образование Индекс Джини оценивает неравенство в образовании для данного населения. Он используется для определения тенденций в социальном развитии по уровню образования с течением времени. Из исследования 85 стран, проведенного тремя экономистами Всемирного банка Винодом Томасом, Яном Вангом и Сибо Фаном, по оценке Мали, самый высокий индекс Джини в области образования в 1990 году составлял 0,92 (что означает очень высокое неравенство в уровне образования среди населения), в то время как в Соединенных Штатах имеет самый низкий показатель неравенства в образовании, индекс Джини 0,14. В период с 1960 по 1990 год индекс Джини неравенства в образовании снизился в Китае, Индии и Южной Корее. Они также утверждают, что индекс Джини в сфере образования в США за период 1980–1990 гг. Немного вырос.
Возможность
Подобно коэффициенту Джини дохода, коэффициент Джини возможностей измеряет неравенство возможностей. Эта концепция основана на предложении Амартии Сена о том, что коэффициенты неравенства в социальном развитии должны основываться на процессе расширения возможностей людей и расширении их возможностей, а не на процессе сокращения неравенства доходов. Ковачевич в обзоре возможностей Коэффициент Джини объясняет, что коэффициент оценивает, насколько хорошо общество позволяет своим гражданам добиваться успеха в жизни, где успех основан на выборе, усилиях и талантах человека, а не на его опыте, определяемом набором заранее определенных обстоятельств. рождение, например, пол, раса, место рождения, доход родителей и обстоятельства, не зависящие от этого человека.
В 2003 году Ремер сообщил, что Италия и Испания продемонстрировали самый высокий индекс неравенства возможностей Джини среди стран с развитой экономикой.
Мобильность доходов
Индекс Шоррокса рассчитывается различными способами, общий подход основан на соотношении коэффициентов Джини дохода между краткосрочными и долгосрочными доходами для одного и того же региона или страны.
Функции
У коэффициента Джини есть особенности, которые делают его полезным для измерения дисперсии населения и, в частности, неравенства.
Ограничения
| Бытовая группа | Страна A Годовой доход ($) | Годовой доход страны B ($) |
|---|---|---|
| 1 | 20 000 | 9 000 |
| 2 | 30 000 | 40 000 |
| 3 | 40 000 | 48 000 |
| 4 | 50 000 | 48 000 |
| 5 | 60 000 | 55 000 |
| Общая прибыль | 200 000 долл. США | 200 000 долл. США |
| Джини страны | 0,2 | 0,2 |
Различные распределения доходов с одинаковым коэффициентом Джини
Крайнее неравенство в благосостоянии, но низкий коэффициент Джини дохода
Индекс Джини не содержит информации об абсолютных национальных или личных доходах. У населения могут быть очень низкие индексы Джини дохода, но одновременно очень высокий индекс Джини благосостояния. Измеряя неравенство в доходах, индекс Джини игнорирует дифференциальную эффективность использования дохода домохозяйства. Игнорируя богатство (за исключением того, что оно способствует доходу), индекс Джини может создать видимость неравенства, когда сравниваемые люди находятся на разных этапах своей жизни. В богатых странах, таких как Швеция, может быть низкий коэффициент Джини для располагаемого дохода, равный 0,31, таким образом, они кажутся равными, но при этом имеют очень высокий коэффициент Джини для богатства от 0,79 до 0,86, что свидетельствует о крайне неравном распределении богатства в их обществе. Эти факторы не оцениваются в индексе Джини, основанном на доходе.
Индекс Джини имеет тенденцию к понижению для небольших групп населения. Графства, штаты или страны с небольшой численностью населения и менее разнообразной экономикой, как правило, сообщают низкие коэффициенты Джини. Для экономически разнообразных больших групп населения ожидается гораздо более высокий коэффициент, чем для каждого из ее регионов. Взяв, например, мировую экономику и распределение доходов для всех людей, разные ученые оценивают глобальный индекс Джини в диапазоне от 0,61 до 0,68. Как и в случае с другими коэффициентами неравенства, на коэффициент Джини влияет степень детализации измерений. Например, пять 20% квантилей (низкая степень детализации) обычно дают более низкий коэффициент Джини, чем двадцать 5% квантилей (высокая степень детализации) для того же распределения. Филипп Монфор показал, что использование непоследовательной или неопределенной детализации ограничивает полезность измерений коэффициента Джини.
Коэффициент Джини дает разные результаты при применении к отдельным лицам, а не домашним хозяйствам, для одной и той же экономики и одинакового распределения доходов. Если используются данные домохозяйства, измеренное значение дохода Джини зависит от того, как определяется домохозяйство. Когда разные популяции не измеряются с помощью последовательных определений, сравнение не имеет смысла.
| Уровень дохода (в скорректированных долларах 2010 г.) | % населения 1979 г. | % населения 2010 г. |
|---|---|---|
| Менее 15 000 долларов США | 14,6% | 13,7% |
| 15 000–24 999 долларов США | 11,9% | 12,0% |
| 25 000–34 999 долларов США | 12,1% | 10,9% |
| 35 000–49 999 долл. США | 15,4% | 13,9% |
| 50 000–74 999 долл. США | 22,1% | 17,7% |
| 75 000–99 999 долл. США | 12,4% | 11,4% |
| 100 000–149 999 долл. США | 8,3% | 12,1% |
| 150 000–199 999 долл. США | 2,0% | 4,5% |
| 200 000 долларов США и больше | 1,2% | 3,9% |
| Всего домохозяйств | 80 776 000 | 118 682 000 |
| Джини США до налогообложения | 0,404 | 0,469 |
Коэффициент Джини не позволяет различить эффекты структурных изменений в популяциях.
Говоря о важности показателей продолжительности жизни, коэффициент Джини как точечная оценка равенства в определенный момент времени игнорирует изменения дохода в течение продолжительности жизни. Как правило, увеличение доли молодых или старых членов общества приводит к очевидным изменениям в равенстве просто потому, что люди, как правило, имеют более низкие доходы и благосостояние в молодом возрасте, чем в старом. Из-за этого такие факторы, как возрастное распределение внутри населения и мобильность внутри классов дохода, могут создавать видимость неравенства, когда его не существует, с учетом демографических эффектов. Таким образом, данная экономика может иметь более высокий коэффициент Джини в любой момент времени по сравнению с другим, в то время как коэффициент Джини, рассчитанный на основе дохода людей на протяжении всей жизни, на самом деле ниже, чем у явно более равной (в данный момент времени) экономики. По сути, имеет значение не только неравенство в конкретном году, но и структура распределения во времени.
Квок утверждает, что коэффициент Джини дохода в Гонконге был высоким (0,434 в 2010 году), отчасти из-за структурных изменений в его населении. За последние десятилетия Гонконг стал свидетелем увеличения числа небольших домашних хозяйств, пожилых людей и пожилых людей, живущих в одиночестве. Совокупный доход теперь разделен на большее количество домохозяйств. Многие пожилые люди живут отдельно от своих детей в Гонконге. Эти социальные изменения вызвали существенные изменения в распределении доходов домохозяйств. Коэффициент дохода Джини, утверждает Квок, не учитывает эти структурные изменения в обществе. Распределение денежных доходов домохозяйств в США, краткое изложение которого приведено в таблице C этого раздела, подтверждает, что эта проблема не ограничивается только Гонконгом. По данным Бюро переписи населения США, в период с 1979 по 2010 год население Соединенных Штатов претерпело структурные изменения во всех домохозяйствах, доход для всех категорий доходов увеличился с поправкой на инфляцию, распределение доходов домохозяйств с течением времени переместилось в категории с более высокими доходами, в то время как Коэффициент Джини дохода увеличился.
Неспособность оценить выгоды и доход от неформальной экономики влияет на точность коэффициента Джини
Некоторые страны распределяют блага, которые трудно оценить. Страны, которые предоставляют субсидированное жилье, медицинское обслуживание, образование или другие подобные услуги, трудно оценить объективно, поскольку это зависит от качества и размера льгот. В отсутствие свободных рынков оценка этих трансфертов доходов как доходов домохозяйств является субъективной. Теоретическая модель коэффициента Джини ограничивается принятием правильных или неправильных субъективных предположений.
У Джини также есть некоторые математические ограничения. Он не аддитивен, и разные группы людей не могут быть усреднены, чтобы получить коэффициент Джини для всех людей в наборах.
Альтернативы
Связь с другими статистическими показателями
Другое использование
В исследовании 2005 года использовались данные переписи населения США для измерения владения домашним компьютером и использовался коэффициент Джини для измерения неравенства среди белых и афроамериканцев. Результаты показали, что, хотя в целом неравенство владения домашними компьютерами снижается, среди белых домохозяйств оно значительно меньше.
Коэффициент Джини
Коэффициент Джини (Gini coefficient) — это количественный показатель, показывающий степень неравенства различных вариантов распределения доходов, разработанный итальянским экономистом, статистиком и демографом Коррадо Джини (1884-1965 гг.).
Чем выше неравенство в распределении доходов, тем больше коэффициент приближается к единице (абсолютное неравенство). И чем выше равенство в распределении доходов, тем меньше данный коэффициент. При абсолютном равенстве он достигает нуля. Системы прогрессивного налогообложения и трансфертных платежей приближают «кривую Лоренца» к биссектрисе. Опыт развитых стран свидетельствует, что неравенство в распределении доходов со временем сокращается. В нашей стране дифференциация доходов населения представлена в таблице (в сравнении с США).
Дифференциация доходов населения России и США, 1996 г.
| Показатель | Россия | США |
| Денежные доходы, в том числе по 20-ти процентным группам населения: | 100 | 100 |
| первая (с наименьшими доходами) | 6,5 | 4,7 |
| вторая | 10,9 | 11,0 |
| третья | 15,5 | 17,4 |
| четвертая | 22,4 | 25,0 |
| пятая (с наивысшими доходами) | 44,7 | 41,9 |
| Коэффициент Джини | 0,375 | — |
| Соотношение доходов 10% наиболее и наименее обеспеченного населения, раз | 13,0 | 10,0 |
Данные таблицы рассчитаны только по учтенным доходам, которые в России составляют менее 60% от всей суммы доходов. О дифференциации доходов населения можно судить по соотношению доходов 10% наиболее обеспеченных и 10% наименее обеспеченного населения. Государство проводит социальную политику распределения доходов с тем, чтобы соотношение данных групп населения не превышало 7 (по мнению некоторых экономистов, данное соотношение считается оптимальным). В нашей стране по официальным данным этот показатель равен 13, а по неофициальным — достигает 25 и более.
Основы экономической теории. Курс лекций. Под редакцией Баскина А.С., Боткина О.И., Ишмановой М.С. Ижевск: Издательский дом «Удмуртский университет», 2000.
Коэффициент Джини
Коэффициент Джини (0÷1), индекс Джини (0÷100 %)
| 0.25–0.29 | 0.30–0.34 0.35–0.39 0.40–0.44 | 0.45–0.49 0.50–0.54 0.55–0.59 ≥ 0.60 | нет данных |
Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку.
Иногда используется процентное представление этого коэффициента, называемое индексом Джини.
Иногда коэффициент Джини (как и кривую Лоренца) используют также и для выявления уровня неравенства по накопленному богатству, однако в таком случае необходимым условием становится неотрицательность чистых активов домохозяйства.
Содержание
История вопроса
Эта статистическая модель была предложена и разработана итальянским статистиком и демографом Коррадо Джини (1884—1965) и опубликована в 1912 году в его труде «Вариативность и изменчивость признака» («Изменчивость и непостоянство»).
Расчёт
Рассчитать коэффициент можно как отношение площади фигуры, образованной кривой Лоренца и кривой равенства, к площади треугольника, образованного кривыми равенства и неравенства. Иначе говоря, следует найти площадь первой фигуры и поделить её на площадь второй. В случае полного равенства коэффициент будет равен 0; в случае полного неравенства он будет равен 1.
Иногда используют индекс Джини — процентное представление коэффициента Джини.
Коэффициент Джини можно рассчитать по формуле Брауна:

или по формуле Джини:

Преимущества коэффициента Джини
Недостатки коэффициента Джини
Пример расчета коэффициента Джини
Предварительный коэффициент в 2010 году 42 % (0,420) [3] Коэффициент Джини в России в 2009 году составлял 42,2 % (0.422), в 2001 году 39,9 % (0.399) [4] В 2012 по данным Global Wealth Report Россия опережает все крупные страны и имеет коэффициент 0,84
См. также
Примечания
Полезное
Смотреть что такое «Коэффициент Джини» в других словарях:
КОЭФФИЦИЕНТ ДЖИНИ — (Gini coefficient) Статистический показатель неравенства. Например, если уi – доход i го человека, коэффициент Джини равен половине ожидаемой абсолютной разницы между доходами двух случайно выбранных человек, i и j, деленной на средний доход. На… … Экономический словарь
КОЭФФИЦИЕНТ ДЖИНИ — коэффициент, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютного равного их распределения между всеми жителями страны. См. т.ж. ИНДЕКС КОНЦЕНТРАЦИИ ДОХОДОВ … Энциклопедический словарь экономики и права
КОЭФФИЦИЕНТ ДЖИНИ — показатель, характеризующий степень отклонения фактического распределения доходов от абсолютного равенства или абсолютного неравенства. Если у всех граждан доходы одинаковы, то К.Д. равен нулю, если же допустить гипотезу, что весь доход… … Большой экономический словарь
Коэффициент Джини — индекс концентрации доходов, показывающий характер распределения всей суммы доходов населения между его отдельными группами … Социология: словарь
Коэффициент Джини — показатель концентрации доходов населения; чем выше неравенство в обществе, тем он ближе к 1 … Экономика: глоссарий
коэффициент джини — макроэкономический показатель, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютного равного их распределения между жителями страны … Словарь экономических терминов
Индекс концентрации доходов (Коэффициент Джини) — Index of concentration of incomes, Income concentration index, Gini coefficient Макроэкономический показатель, характеризующий дифференциацию денежных доходов населения в виде степени отклонения фактического распределения доходов от абсолютно… … Словарь бизнес-терминов
Джини коэффициент — индекс концентрации доходов индекс Джини Показатель, характеризующий неравенство доходов населения, т.е. степень отклонения фактического распределения денежных доходов от равномерного. Д.к. рассчитывается с помощью т.н. кривой Лоренца (см. рис. к … Справочник технического переводчика
Джини коэффициент — ( индекс концентрации доходов, индекс Джини)[Gini coefficient] показатель, характеризующий неравенство доходов населения, т.е. степень отклонения фактического распределения денежных доходов от равномерного. Д.к. рассчитывается с помощью т.н.… … Экономико-математический словарь