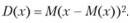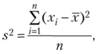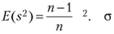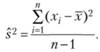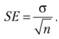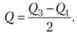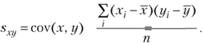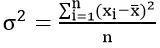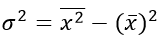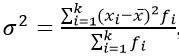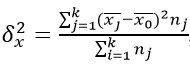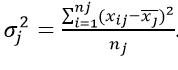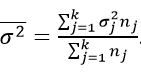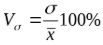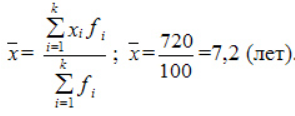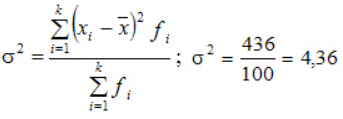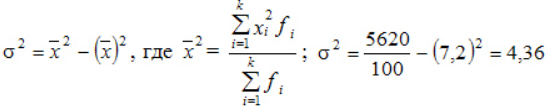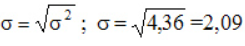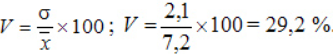О чем говорит дисперсия

Дисперсия и стандартное отклонение

Дисперсия случайной величины — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. В статистике для обозначения дисперсии часто употребляется обозначение (сигма в квадрате). Квадратный корень из дисперсии , равный , называется стандартным отклонением или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Хотя для оценки всей выборки очень удобно использовать лишь одно значение (такое как среднее значение или моду и медиану), этот подход легко может привести к неправильным выводам. Причина такого положения лежит не в самой величине, а в том, что одна величина никак не отражает разброс значений данных.

Например, в выборке:

среднее значение равно 5.

Однако, в самой выборке нет ни одного элемента со значением 5. Возможно, Вам потребуется знать степень близости каждого элемента выборки к ее среднему значению. Или, другими словами, вам потребуется знать дисперсию значений. Зная степень изменения данных, Вы можете лучше интерпретировать среднее значение, медиану и моду. Степень изменения значений выборки определяется путем вычисления их дисперсии и стандартного отклонения.

Дисперсия и квадратный корень из дисперсии, называемый стандартным отклонением, характеризуют среднее отклонение от среднего значения выборки. Среди этих двух величин наибольшее значение имеет стандартное отклонение. Это значение можно представить как среднее расстояние, на котором находятся элементы от среднего элемента выборки.

Дисперсию трудно интерпретировать содержательно. Однако, квадратный корень из этого значения является стандартным отклонением и хорошо поддается интерпретации.

Стандартное отклонение вычисляется путем определения сначала дисперсии и затем вычисления квадратного корня из дисперсии.

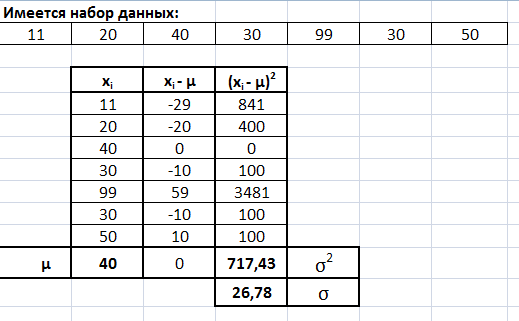
Например, для массива данных, приведенных на рисунке, будут получены следующие значения:

Здесь среднее значение квадратов разностей равно 717,43. Для получения стандартного отклонения осталось лишь взять квадратный корень из этого числа.

Результат составит приблизительно 26,78.

Следует помнить, что стандартное отклонение интерпретируется как среднее расстояние, на котором находятся элементы от среднего значения выборки.

Стандартное отклонение показывает, насколько хорошо среднее значение описывает всю выборку.

Допустим, Вы являетесь руководителем производственного отдела по сборке ПК. В квартальном отчете говорится, что выпуск за последний квартал составил 2500 ПК. Плохо это или хорошо? Вы попросили (или уже в отчете есть эта графа) в отчете отобразить стандартное отклонение по этим данным. Цифра стандартного отклонения, например, равна 2000. Становится понятным для Вас, как руководителя отдела, что производственная линия требует лучшего управления (слишком большие отклонения по количеству собираемых ПК).

Вспомним: при большой величине стандартного отклонения данные широко разбросаны относительно среднего значения, а при маленькой – они группируются близко к среднему значению.

Четыре статистические функции ДИСП(), ДИСПР(), СТАНДОТКЛОН() и СТАНДОТКЛОНП() – предназначены для вычисления дисперсии и стандартного отклонения чисел в интервале ячеек. Перед тем как вычислять дисперсию и стандартное отклонение набора данных, нужно определить, представляют ли эти данные генеральную совокупность или выборку из генеральной совокупности. В случае выборки из генеральной совокупности следует использовать функции ДИСП() и СТАНДОТКЛОН(), а в случае генеральной совокупности – функции ДИСПР() и СТАНДОТЛОНП():

Генеральная совокупность	Функция
	ДИСПР()
	СТАНДОТЛОНП()
Выборка
	ДИСП()
	СТАНДОТКЛОН()

Дисперсия (а так же стандартное отклонение), как мы отмечали, свидетельствуют о том, в какой степени входящие в набор данных величины разбросаны вокруг среднего арифметического.

Малое значение дисперсии или стандартного отклонения говорит о том, что все данные сосредоточены вокруг среднего арифметического, а большое значение этих величин – о том, что данные разбросаны в широком диапазоне значений.

Дисперсию достаточно трудно интерпретировать содержательно (что значит малое значение, большое значение?). Выполнение Задания 3позволит визуально, на графике, показать смысл дисперсии для набора данных.

Задания

· 2.1. Дать понятия: дисперсия и стандартное отклонение; их символьное обозначение при статистической обработке данных.

· 2.2. Оформить рабочий лист в соответствии с рисунком 1 и произвести необходимые расчеты.

· 2.3. Привести основные формулы, используемые при расчетах

· 2.4. Пояснить все обозначения ( , , , )

· 2.5. Пояснить практическое значение понятия дисперсия и стандартное отклонение.

Задание 2.

1.1. Дать понятия: генеральная совокупность и выборка; математическое ожидание и среднее арифметическое их символьное обозначение при статистической обработке данных.

1.2. В соответствии с рисунком 2 оформить рабочий лист и произвести расчеты.

1.3. Привести основные формулы, используемые при расчетах (для генеральной совокупности и выборке).

1.4. Объяснить, почему возможны получения таких значений средних арифметических в выборках как 46,43 и 48,78 (см. файл Приложение). Сделать выводы.

Задание 3.

Имеется две выборки с различным набором данных, но среднее для них будет одинаковым:

Рисунок 4	Рисунок 5
Видно, что практически разброса нет. Значение дисперсии 0,008 и стандартного отклонения – 0,089. Все очень наглядно.	Разброс данных явный, что подтверждает значение дисперсии – 2,19 и стандартного отклонения – 1,709

3.1. Оформить рабочий лист в соответствии с рисунком 3 и произвести необходимые расчеты.

3.2. Приведите основные формулы расчета.

3.3. Постройте графики в соответствии с рисунками 4, 5.

3.4. Поясните полученные зависимости.

3.5. Аналогичные вычисления проведите для данных двух выборок.

Исходная выборка 11119999

Значения второй выборки подбираете так, что бы среднее арифметическое для второй выборки было таким же, например,:

Подберите значения для второй выборки самостоятельно. Оформите вычисления и построения графиков подобно рисункам 3, 4, 5. Покажите основные формулы, которые использовали при вычислениях.

Сделайте соответствующие выводы.

Все задания оформить в виде отчета со всеми необходимыми рисунками, графиками, формулами и краткими пояснениями.

Примечание: построение графиков обязательно пояснить с рисунками и краткими пояснениями.

Источник

Дисперсия и ее оценка

Определение дисперсии случайных величин

Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.

В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:

где М(х) – математическое ожидание, а D(х) – дисперсия.

На основе данной формулы можно вывести другую, которая дает оценку дисперсии:

В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.

Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:

Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности. Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения. При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:

Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.

Характеристика оценивания стандартного отклонения

Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением. Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности. Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:

где SE – стандартная ошибка.

Данная статистика необходима для интервальной оценки исследуемой случайной величины.

Характеристика оценки полумежквартильного интервала

Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.

Квартиль – это вариант названия квантиля распределения.

При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:

Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.

Характеристика ковариации

Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:

Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах. Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция». Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.

Источник

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

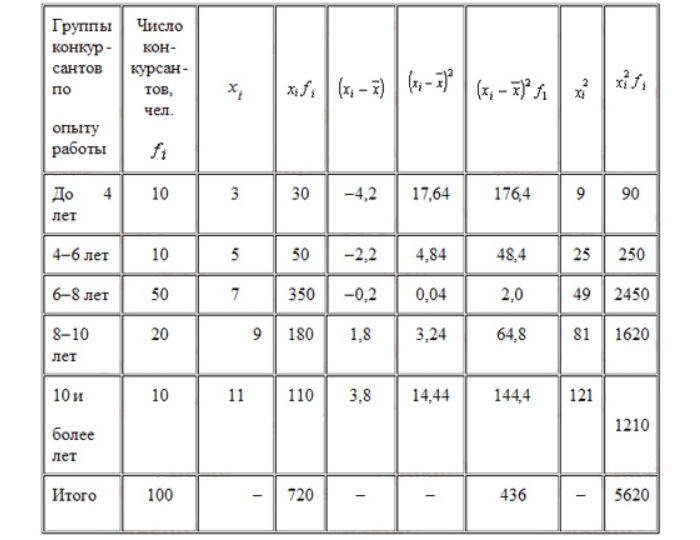
Пример расчета дисперсии

Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Источник