О чем гласит теорема виета

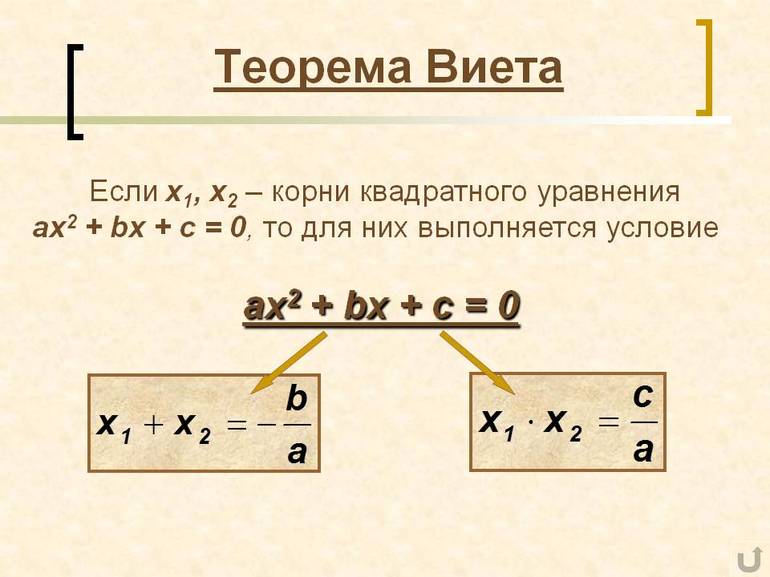
Теорема Виета

В математике существуют специальные приемы, с которыми многие квадратные уравнения решаются очень быстро и без всяких дискриминантов. Более того, при надлежащей тренировке многие начинают решать квадратные уравнения устно, буквально «с первого взгляда».

К сожалению, в современном курсе школьной математики подобные технологии почти не изучаются. А знать надо! И сегодня мы рассмотрим один из таких приемов — теорему Виета. Для начала введем новое определение.

Правда, далеко не всегда эти преобразования будут полезны для отыскания корней. Чуть ниже мы убедимся, что делать это надо лишь тогда, когда в итоговом приведенном квадратом уравнении все коэффициенты будут целочисленными. А пока рассмотрим простейшие примеры:

Задача. Преобразовать квадратное уравнение в приведенное:

Как видите, приведенные квадратные уравнения могут иметь целые коэффициенты даже в том случае, когда исходное уравнение содержало дроби.

Теперь сформулируем основную теорему, для которой, собственно, и вводилось понятие приведенного квадратного уравнения:

. Рассмотрим приведенное квадратное уравнение вида x 2 + bx + c = 0. Предположим, что это уравнение имеет действительные корни x ₁ и x ₂. В этом случае верны следующие утверждения:

Примеры. Для простоты будем рассматривать только приведенные квадратные уравнения, не требующие дополнительных преобразований:

Теорема Виета дает нам дополнительную информацию о корнях квадратного уравнения. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь «видеть» корни и буквально угадывать их за считанные секунды.

Задача. Решите квадратное уравнение:

Попробуем выписать коэффициенты по теореме Виета и «угадать» корни:

Из приведенных рассуждений видно, как теорема Виета упрощает решение квадратных уравнений. Никаких сложных вычислений, никаких арифметических корней и дробей. И даже дискриминант (см. урок «Решение квадратных уравнений») нам не потребовался.

Разумеется, во всех размышлениях мы исходили из двух важных предположений, которые, вообще говоря, не всегда выполняются в реальных задачах:

Однако в типичных математических задачах эти условия выполняются. Если же в результате вычислений получилось «плохое» квадратное уравнение (коэффициент при x 2 отличен от 1), это легко исправить — взгляните на примеры в самом начале урока. Про корни вообще молчу: что это за задача, в которой нет ответа? Конечно, корни будут.

Таким образом, общая схема решения квадратных уравнений по теореме Виета выглядит следующим образом:

Задача. Решите уравнение: 5 x 2 − 35 x + 50 = 0.

Итак, перед нами уравнение, которое не является приведенным, т.к. коэффициент a = 5. Разделим все на 5, получим: x 2 − 7 x + 10 = 0.

Все коэффициенты квадратного уравнения целочисленные — попробуем решить по теореме Виета. Имеем: x ₁ + x ₂ = −(−7) = 7; x ₁ · x ₂ = 10. В данном случае корни угадываются легко — это 2 и 5. Считать через дискриминант не надо.

Задача. Решите уравнение: −5 x 2 + 8 x − 2,4 = 0.

Смотрим: −5 x 2 + 8 x − 2,4 = 0 — это уравнение не является приведенным, разделим обе стороны на коэффициент a = −5. Получим: x 2 − 1,6 x + 0,48 = 0 — уравнение с дробными коэффициентами.

Задача. Решите уравнение: 2 x 2 + 10 x − 600 = 0.

Для начала разделим все на коэффициент a = 2. Получится уравнение x 2 + 5 x − 300 = 0.

Это приведенное уравнение, по теореме Виета имеем: x ₁ + x ₂ = −5; x ₁ · x ₂ = −300. Угадать корни квадратного уравнения в данном случае затруднительно — лично я серьезно «завис», когда решал эту задачу.

Теперь, когда корень из дискриминанта известен, решить уравнение не составит труда. Получим: x ₁ = 15; x ₂ = −20.

Источник

Теорема Виета.

Формулы Виета — это формулы, которые выражают коэффициенты многочлена через его корни.

Эти формулы хорошо использовать для сверки правильности определения корней многочлена. Еще их

используют для выведения многочлена из заданных корней.

С помощью теоремы Виета решаются квадратные уравнения.

Если наибольший коэффициент многочлена , т.е. многочлен не приведенный, значит, для

использования формулы Виета нужно сначала поделить все коэффициенты на (это не сказывается на

значении корней многочлена). В таком случае формулы Виета дают выражение для отношений всех

коэффициентов к наибольшему.

Формулировка теоремы Виета для квадратного трехчлена.

Для приведенного квадратного уравнения (такого, коэффициент при x 2 в котором = 1): сумма корней

приведённого квадратного уравнения равна коэффициенту со знаком «-», а

произведение корней = свободному члену .

В общем случае – для не приведённого квадратного уравнения:

Пользуясь этой теоремой, легко находить корни некоторых квадратных уравнений в уме.

Смысл теоремы Виета состоит в том, что, не зная корней квадратного трехчлена, запросто можно вычислить

их сумму и произведение – простейшие симметричные многочлены от двух переменных и .

Теорема Виета дает угадывать целые корни квадратного трехчлена.

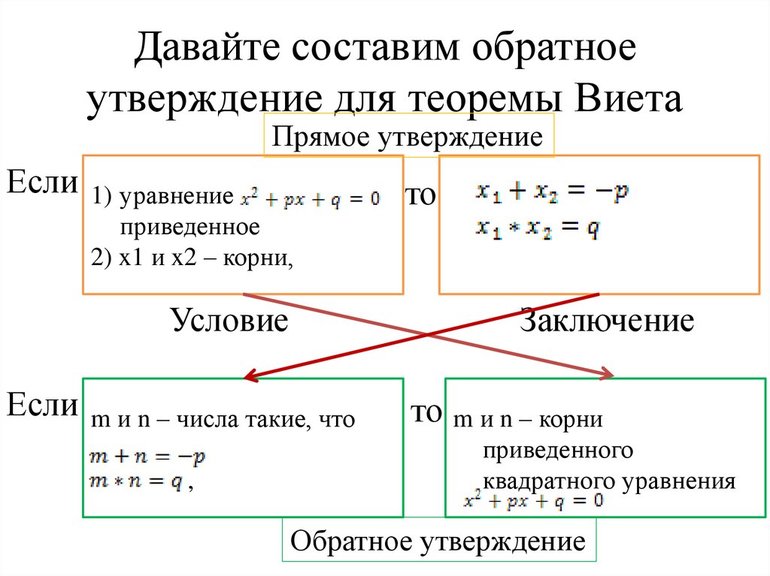
Обратная теорема Виета.

Если числа и удовлетворяют соотношениям , то они удовлетворяют

квадратному уравнению , то есть являются его корнями.

Даны числа и — корни некоторого квадратного уравнения. Необходимо составить

Предположим наше квадратное уравнение выглядит так:

Значит, согласно теореме Виета, его коэффициенты связаны с корнями таким соотношениями:

Таким образом квадратное уравнение:

Ответ:

Общая формулировка теоремы Виета.

Если — корни многочлена (все корни взяты

соответствующее их кратности количество раз), то коэффициенты выражают в виде

симметрических многочленов от корней, как показано ниже:

Другими словами, произведение соответствует сумме всех возможных произведений из корней.

Источник

Теорема Виета

Теорема Виета — это теорема, которая используется для решения квадратных уравнений.

В уравнении вида x²+px+q = 0:

Пример 1

p- это второй коэффициент с противоположным знаком

q- это третий коэффициент

Надо подобрать корни x1 и x2 таким образом, чтобы их сумма равнялась −5, но и их произведение равнялось −6 (обычно это делается в уме).

Пример 2

Надо подобрать корни x1 и x2 таким образом, чтобы их сумма равнялась 4,5, но и произведение равнялось бы 2.

Единственные числа, которые сюда подходят — это 4 и 0,5, значит x1 = 4 и x2 = 0,5.

Обратная теорема Виета

Если числа x1 и x2 являются корнями квадратного уравнения вида x² + px + q = 0, то известно, что x1+x2 = −p и x1. x2 = q.

Известны x1 = 4 и x2 = 3, корни квадратного уравнения. Требуется составить это уравнение.

Искомое уравнение имеет вид x² + px + q = 0

p = −(x1+x2) = −(4+3) = −7 (не забудьте про минус)

Уже есть все значения, можно составить искомое уравнение: x² − 7x + 12 = 0.

Теорема Виета для кубического уравнения

Имеется уравнение вида ax³ + bx² + cx + d = 0

В этом случае будут подбираться корни, удовлетворяющие эти условия:

Где x1, x2, x3 — корни уравнения.

Как превратить неприведённое квадратное уравнение в приведённое

Если уравнение выглядит так: ax² + bx + c = 0 (вместе с x² стоит число), то это уравнение является неприведённым, с ним ещё нельзя работать. Чтобы сделать его приведённым, нужно всего лишь разделить всё уравнение на это число a.

Например:

Если вам неизвестны коэффициенты, это деление можно показать так:

Источник

Общие сведения

Для применения формул теоремы Виета для квадратного уравнения следует разобрать некоторые термины и математические определения. Квадратным уравнением вида Am 2 + Bm + C = 0 называется многочлен второй степени, состоящий из коэффициента А при некоторой неизвестной в квадрате и суммы произведения второго коэффициента на неизвестную величину и константы С. Этот многочлен преобразовывается в уравнение только при равенстве нулевому значению. Константу С еще называют свободным членом.

Корнями называются такие значения неизвестных, при подстановке которых тождество считается верным. Следует отметить, что в результате отдельных математических преобразований появляются дополнительные корни. Особенно это касается различных замен в тригонометрических функциях. Однако при подстановке корней равенство не соблюдается. Математики называют их ложными. После решения уравнения специалисты рекомендуют произвести подстановку этих значений в исходное уравнение. Этот прием помогает избавиться от нежелательных решений.

Поиск корней при помощи теоремы Виета принадлежит к быстрым методикам, поскольку избавляет человека от ненужных расчетов по формулам с применением дискриминанта.

Виды квадратных уравнений

Квадратные уравнения бывают нескольких видов, поскольку не во всех случаях коэффициенты получаются отличными от нуля. Математики классифицировали их на 2 типа:

Первыми называются выражения со всеми коэффициентами (A, B и C), отличными от нуля. Если число перед неизвестной не указано, то считается, что оно эквивалентно 1. Неполными считаются любые уравнения, в которых отсутствует B или C. Однако бывают случаи, когда оба последних коэффициента соответствуют нулю, тогда тождество имеет следующий вид: Am 2 = 0. Кроме того, существует еще один критерий распределения на виды, основанный на степени приведенности. По этому признаку выражения делятся на приведенные и неприведенные классы.

К первым следует отнести любые равенства, у которых коэффициент равен 1. Во всех остальных случаях (А > 1) тождества являются неприведенными.

Условие использования закона

Закон Виета применим не ко всем уравнениям. Математики сформулировали важные условия, при соблюдении которых возможно воспользоваться этим правилом: уравнение должно быть приведенным и иметь значение дискриминанта больше 0. Из этого условия можно сделать вывод: когда равенство невозможно преобразовать к приведенному, следует применять другие методики нахождения корней, а не правило Виета.

Существует простой алгоритм преобразования уравнения к необходимому виду. Для этого нужно выполнить несложную операцию деления каждого коэффициента на А. Например, следует преобразовать уравнение 4p 2 + 8p + 16 = 0 в приведенное. Следуя описанному алгоритму, получается такое соотношение: [(4p 2 ) / 4] + [8p / 4] + [16 / 4] = 4p 2 + 2p + 4 = 0.

Специалисты рекомендуют избегать ситуаций получения обыкновенных дробей в результате преобразования. Примером является тождество 3p 2 + 2p — 4 = 0. Его можно свести к приведенному, но применить теорему будет весьма сложно, поскольку равенство будет иметь такой вид: p 2 + (2p / 3) — (4 / 3) = 0. Рекомендуется решать такие уравнения, используя другие методики (построение графика функции, при помощи программ или по формуле дискриминанта).

Применение теоремы

Формулировка закона Виета для квадратного уравнения Am 2 + Bm + C = 0 следующая: сумма корней соответствует коэффициенту А, взятому с противоположным знаком, а результат произведения эквивалентен свободному члену С. Решение осуществляется методом подбора соответствующих числовых значений. Однако каждая теорема должна доказываться.

Далее нужно найти сумму m1 и m2: [-B — D^(½)] / (2 * A) + [-B + D^(½)] / (2 * A). Чтобы упростить полученное выражение, следует воспользоваться таким алгоритмом:

После этого нужно доказать, что произведение корней эквивалентно С. Для этого необходимо перемножить m1 = [-B — D^(½)] / (2 * A) и m2 = [-B + D^(½)] / (2 * A), воспользовавшись правилом умножения дробей обыкновенного типа по такой методике:

Вторая формула доказана. Однако перед решением обязательно следует вычислить значение дискриминанта, поскольку при D = 0 уравнение имеет только один корень. Существует обратная теорема Виета. У нее такая формулировка: если сумма чисел m1 и m2 соответствует некоторому значению В, взятому с противоположным знаком, а также их произведение эквивалентно свободному члену многочлена второй степени, значит, они являются корнями Аm 2 + Bm + C = 0. Это утверждение имеет доказательство, для которого следует выполнить следующие шаги:

Следовательно, теорема доказана, поскольку числа m1 и m2 являются корнями уравнения. Далее нужно рассмотреть приведенные кубические уравнения и порядок применения утверждения Виета.

Кубические равенства с неизвестным

Можно также применять теорему Виета для кубического уравнения вида А * m 3 + B * m 2 + C * m + D = 0. Коэффициент А должен быть равен 1. Находятся корни при помощи перебора значений, но сделать это сложно, поскольку необходимо решить систему, состоящую из трех равенств:

Числа m1, m2 и m3 являются корнями. Кроме того, следует обратить внимание на образование ложных результатов, поскольку уравнение является кубическим. Ученые пришли к выводу о том, что чем выше степень, тем больше образовывается ложных ответов. Они рекомендуют применять специальное программное обеспечение для поиска решения. Если его нет под рукой, то можно построить график функции, а затем найти точки пересечения с осью абсцисс. Существуют также специализированные веб-сервисы. Они называются онлайн-калькуляторами.

Примеры решения

Несмотря на простоту теоремы, существует несколько типов упражнений на эту тему. Они делятся на следующие классы:

К первым следует отнести задачи на простой подбор корней. Средними считаются задания на преобразование квадратного уравнения к приведенному.

Продвинутыми являются любые тождества, которые необходимо упростить и привести к коэффициенту А = 1. Сложные — особый вид. Для них следует применить все знания в области математики. Кроме того, нужно осуществить объяснение хода решения. В некоторых случаях необходимо построить таблицу зависимостей и начертить график.

Интересный факт заключается в том, что именно этот класс выражений существенно развивает умственные способности человека на уроках. Встречаются также задачи на пересечения параболы и прямой, которая может проходить под определенным углом. Далее нужно разобрать практическое применение теоремы Виета на примерах с решением для различных классов задач.

Простой и средний

Пусть дано тождество m 2 — 5 * m + 6 = 0. Необходимо найти его корни. Для решения следует применить такой алгоритм:

Следовательно, тождество решено верно. Далее можно рассмотреть средний тип упражнения. Для этого следует решить уравнение 3 * m 2 + 33 * m + 30 = 0. Найти корни можно по такому алгоритму:

​Следовательно, корни m1 и m2 удовлетворяют этому уравнению. Если не получается делить все члены на А, то необходимо рассмотреть решение с помощью дискриминанта или графическим методом.

Продвинутый класс

На основании шестого пункта можно сделать вывод, что корни подобраны правильно. Этот пример показывает, что одной теоремы недостаточно, поскольку следует уметь выполнять математическое преобразование заданного выражения. В этом классе примеров возможен случай, когда величина дискриминанта эквивалентна 0. Следовательно, у тождества с неизвестным всего один корень. К последнему невозможно применить закон Виета.

Сложные упражнения

Примером сложной задачи, которую еще называют «со звездочкой», является следующая: необходимо найти сумму, произведение и сумму квадратов решений уравнения m 2 — 7 * m + 12 = 0, не находя корней. По обычной методике нужно доказать, что у выражения с неизвестным существует два корня по формуле дискриминанта: D = 49 — 4 * 12 = 1 > 0. Следовательно, ориентируясь на последнее равенство, условие соблюдается. По теореме Виета получаются ответы на первые два вопроса:

Затем следует записать сумму квадратов, используя две описанные выше формулы: (m1)^2 + (m2)^2 = (m1)^2 + (m2)^2 — 2 * m1 * m2 — 2 * m1 * m2 = (m1 + m2)^2 — 2 * m1 * m2 = 7 2 — 2 * 12 = 25. Задача решена: 7; 12 и 25.

Следующий пример является довольно распространенным. Существует уравнение 5 * m 2 — 15 * m + 30 = 0. Необходимо найти сумму кубов корней и квадрат разности. Многие ученики на протяжении всей истории существования алгебры делают однотипную ошибку. Она заключается в подготовке, то есть записываются соответствующие формулы сокращенного умножения. Если их не знают, то пользуются интернетом или другими источниками. На эту операцию тратится драгоценное время. Чтобы этого избежать, необходимо воспользоваться таким алгоритмом:

Источник

Теорема Виета

Теорема Виета:

Сумма корней приведённого квадратного уравнения

равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену

Если приведённое квадратное уравнение имеет вид

то его корни равны:

,

,

а теперь найдём их произведение:

Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:

называются формулами Виета.

Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.

Обратная теорема

Теорема:

Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:

Это доказывает, что число x₁ является корнем уравнения x 2 + px + q = 0. Точно так же можно доказать, что и число x₂ является корнем для этого уравнения.

Решение примеров

Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.

Пример 1. Найти корни уравнения:

очевидно, что корни равны 1 и 2:

Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:

Пример 2. Найти корни уравнения:

С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.

Пример 1. Составить квадратное уравнение по его корням:

Следовательно, искомое уравнение:

Пример 2. Записать приведённое квадратное уравнение, имеющее корни:

Источник