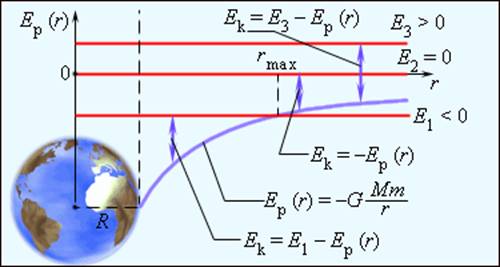
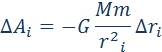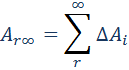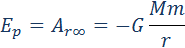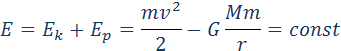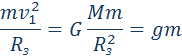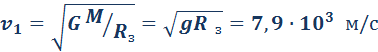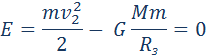Ньютон математически доказал что законы движения планет кеплера являются

Открыт закон движения планет (1618)

Открытые Кеплером три закона движения планет полностью и с превосходной точностью объяснили видимую неравномерность этих движений. Вместо многочисленных надуманных эпициклов модель Кеплера включает только одну кривую — эллипс. Второй закон установил, как меняется скорость планеты при удалении или приближении к Солнцу, а третий позволяет рассчитать эту скорость и период обращения вокруг Солнца.

Законы динамики планет, открытые Кеплером, послужили позже Ньютону основой для создания теории тяготения. Ньютон математически доказал, что все законы Кеплера являются следствиями закона тяготения.

Строго говоря, система мира Кеплера претендовала не только на выявление законов движения планет, но и на гораздо большее. Аналогично пифагорейцам, Кеплер считал мир реализацией некоторой числовой гармонии, одновременно геометрической и музыкальной; раскрытие структуры этой гармонии дало бы ответы на самые глубокие вопросы.

Например, Кеплер объясняет, почему планет именно шесть и они размещены в пространстве так, а не как-либо иначе: оказывается, орбиты планет вписаны в правильные многогранники.

Интересно, что исходя из этих ненаучных соображений, Кеплер предсказал существование двух спутников Марса и промежуточной планеты между Марсом и Юпитером.

Мистическая форма системы Кеплера основательно засоряла реальную суть его великих открытий. Тем не менее, уже современники Кеплера, отделив зерна от шелухи, убедились в точности открытых им законов, хотя их глубинный смысл до Ньютона оставался непонятным. Никаких попыток реанимировать Птолемея или предложить иную систему движения, кроме гелиоцентрической, больше не предпринималось.

Через год после смерти Кеплера Гассенди наблюдал предсказанное им прохождение Меркурия по диску Солнца.

Кеплер стал автором первого учебника по коперниканской астрономии (1622), который немедленно удостоился чести попасть в «Индекс запрещённых книг».

Летом 1627 года Кеплер после 22 лет трудов опубликовал астрономические таблицы, которые в честь императора назвал «Рудольфовыми». Спрос на них был огромен, так как прежние таблицы давно разошлись с наблюдениями. Кеплеровы таблицы служили астрономам и морякам вплоть до начала XIX века.

Источник

Законы Кеплера и их связь с законами Ньютона

Два величайших ученых намного обогнавшие свое время, они создали науку, которая называется небесной механикой, то есть открыли законы движения небесных тел под действием сил тяготения, и даже если бы этим их достижения ограничились, они все равно бы вошли в пантеон великих мира сего. Так случилось, что они не пересеклись во времени. Только через тринадцать лет после смерти Кеплера родился Ньютон. Оба они являлись сторонниками гелиоцентрической системы Коперника. Много лет изучая движение Марса, Кеплер экспериментально открывает три закона движения планет, за пятьдесят с лишним лет до открытия Ньютоном закона всемирного тяготения. Еще не понимая, почему планеты движутся так, а не иначе. Это был каторжный труд и гениальное предвидение. Зато Ньютон именно законами Кеплера проверял свой закон тяготения. Все три закона Кеплера являются следствиями закона тяготения. И открыл его Ньютон в 23 года. В это время 1664 – 1667 годы в Лондоне свирепствовала чума. Тринити колледж, в котором преподавал Ньютон, был распущен на неопределенный срок, дабы не усугубить эпидемию. Ньютон возвращается к себе на родину и за два года совершает переворот в науке, сделав три важнейших открытия: дифференциальное и интегральное исчисление, объяснение природы света и закон всемирного тяготения. Исаак Ньютон был торжественно похоронен в Вестминстерском аббатстве. Над его могилой высится памятник с бюстом и эпитафией «Здесь покоится сэр Исаак Ньютон, дворянин, который почти божественным разумом первый доказал с факелом математики в руке движение планет, пути комет и приливы океанов… Пусть смертные радуются, что существует такое украшение рода человеческого».

Заслуга открытия законов движения планет принадлежит выдающемуся немецкому учёному, астроному и математику, Иоганну Кеплеру (1571 – 1630 гг.)– человеку большого мужества и необыкновенной любви к науке.

Он проявил себя ревностным сторонником системы мира Коперника и задался целью уточнить строение Солнечной системы. Тогда это означало: познать законы движения планет, или, как он выразился, «проследить замысел Бога при cотворении мира» [1]. В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.

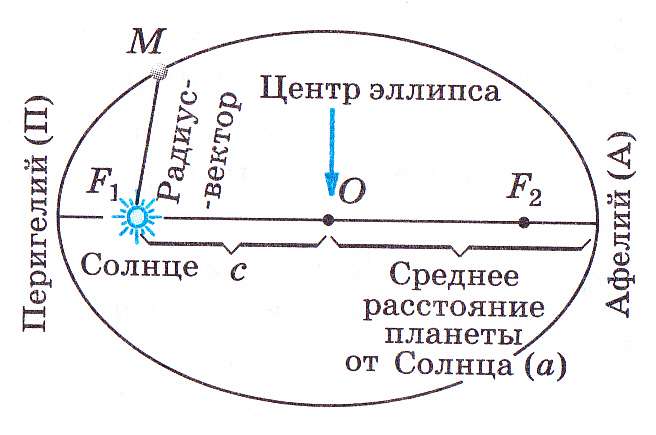
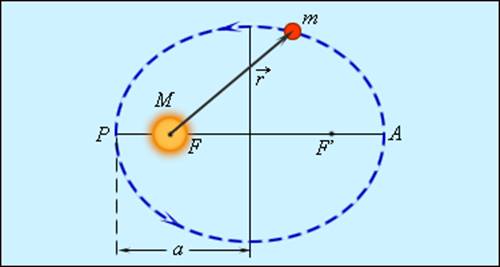
Первый закон Кеплера:Каждая планета обращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

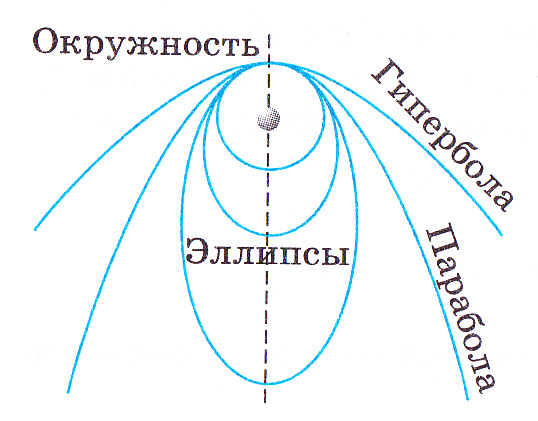
Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений – кругу, эллипсу, параболе или гиперболе. [2 ]

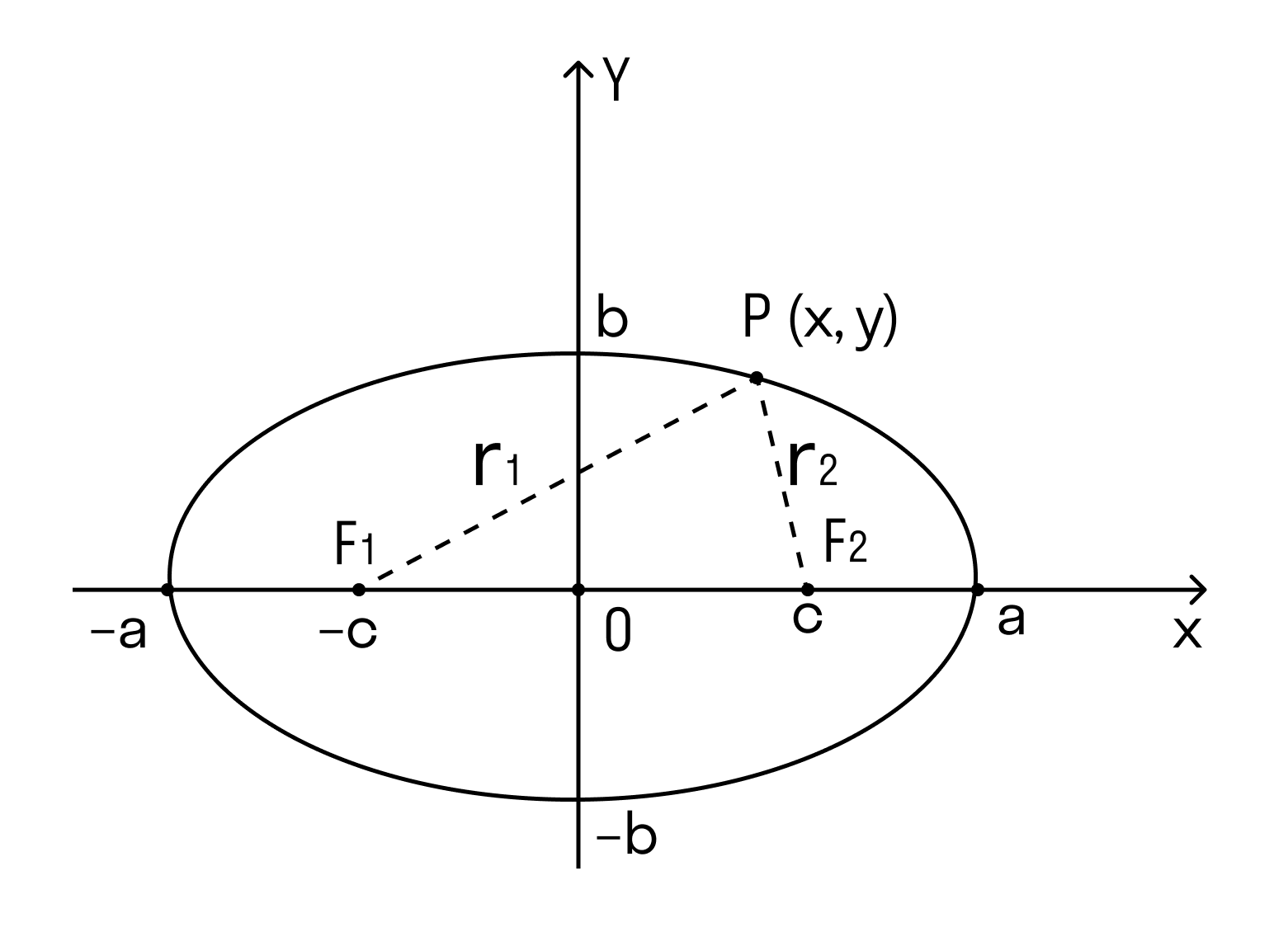
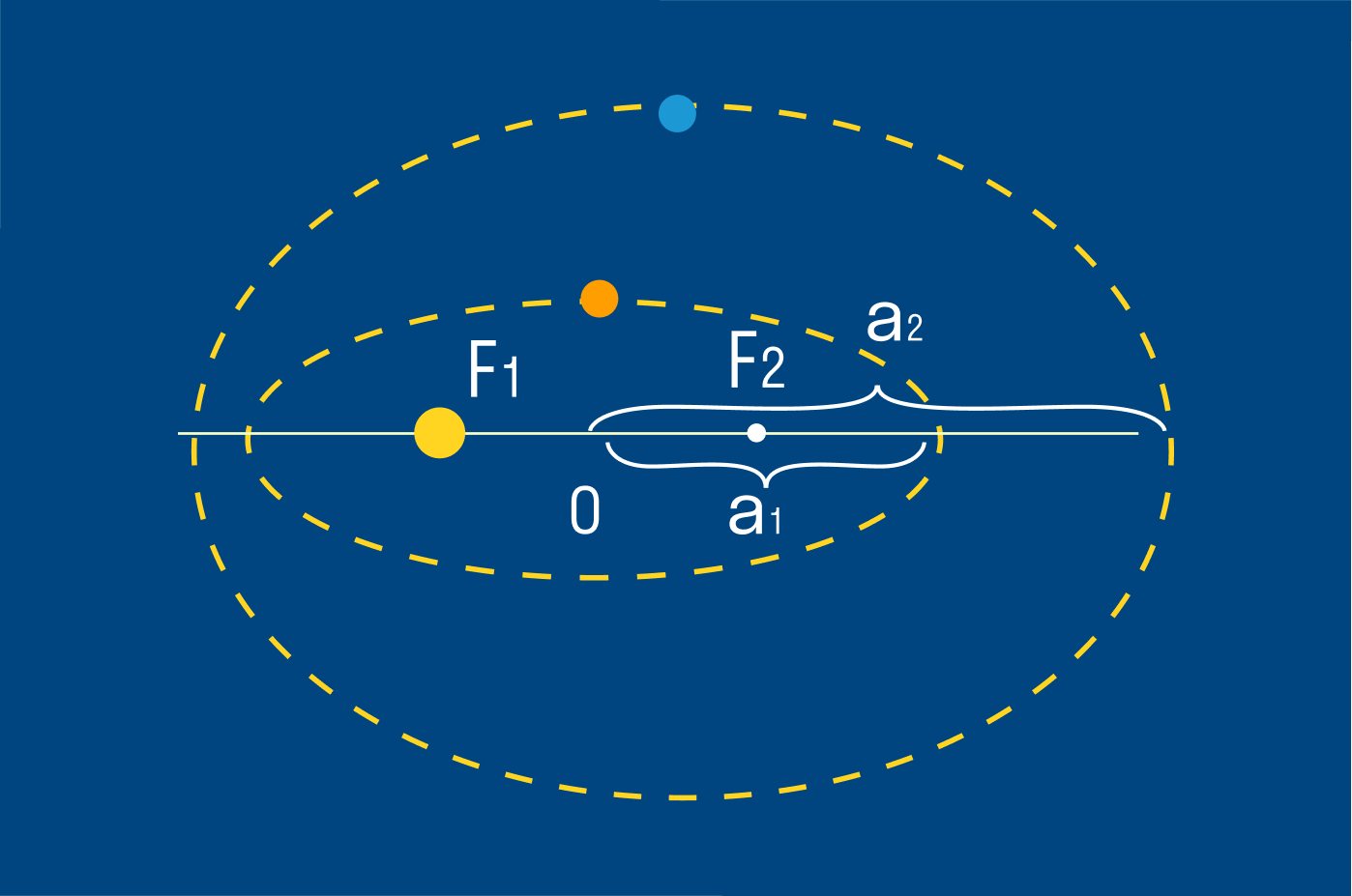
Эллипсом называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой её точки от двух точек, называемых фокусами, остаётся постоянной. Эта сумма расстояний равна длине большой оси эллипса. Точка О – центр эллипса, F1 и F2 – фокусы. Солнце находится в данном случае в фокусе F1.

Ближайшая к Солнцу точка орбиты называется перигелием, самая далёкая – афелием. Линия, соединяющая какую-либо точку эллипса с фокусом, называется радиус-вектором. Отношение расстояния между фокусами к большой оси (к наибольшему диаметру) называется эксцентриситетом е. эллипс тем сильнее вытянут, чем больше его эксцентриситет. Большая полуось эллипса а – среднее расстояние планеты до Солнца.

По эллиптическим орбитам движутся и кометы и астероиды. У окружности е = 0, у эллипса 0 1.

Орбиты планет – эллипсы, мало отличаются от окружностей; их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е = 0,017.

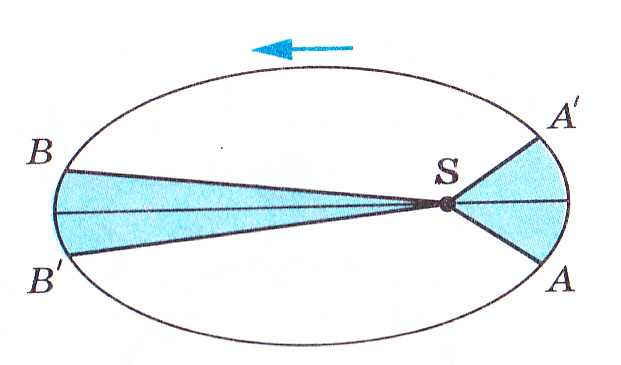
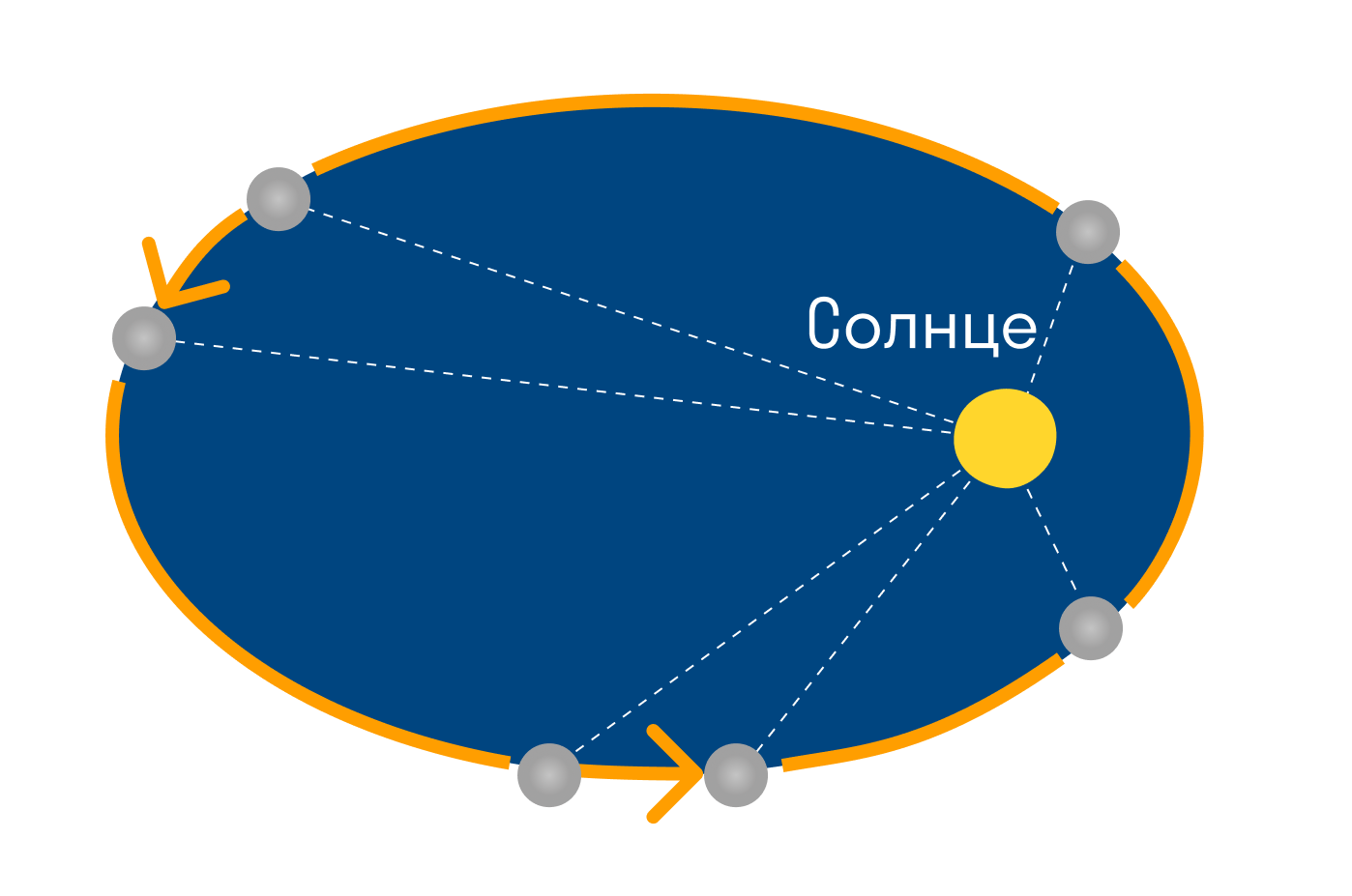
Второй закон Кеплера: Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади (определяет скорость движения планеты по орбите). Скорость планеты тем больше, чем она ближе к Солнцу. [1]

Планета проходит путь от точки А до А1 и от В до В1 за одно и то же время. Другими словами, планета движется быстрее всего в перигелии, а медленнее всего – когда находится на наибольшем удалении (в афелии). Так, скорость кометы Галлея в перигелии равна 55 км/с, а в афелии 0,9 км/с.

Самый близкий к Солнцу Меркурий обегает вокруг светила за 88 дней. За ним движется Венера, и год на ней длится 225 земных суток. Земля обращается вокруг Солнца за 365 суток, то есть ровно за один год. Марсианский год почти в два раза продолжительнее земного. Юпитерский год равен почти 12 земным годам, а далёкий Сатурн обходит свою орбиту за 29,5 лет! Словом, чем дальше планета от Солнца, тем продолжительнее на планете год. И Кеплер пытался найти зависимость между размерами орбит различных планет и временем их обращения вокруг Солнца.

15 мая 1618 года после множества неудачных попыток Кеплер установил наконец очень важное соотношение, известное как

Третий закон Кеплера:Квадраты периодов обращения планет вокруг Солнца относятся как кубы их средних расстояний от Солнца. [1]

Т 2 м / Т 2 з = а 3 _м / а 3 _з.

Но ведь период обращения Земли вокруг Солнца равен одному году (Тз = 1), а среднее расстояние Земля – Солнце принято за одну астрономическую единицу (а_з = 1 а.е.). Тогда данное равенство примет более простой вид:

Период обращения планеты (в нашем примере Марса) можно определить из наблюдений. Он составляет 687 земных суток, или 1,881 года. Зная это, нетрудно вычислить среднее расстояние планеты от Солнца в астрономических единицах:

Т.е. Марс находится в среднем в 1,524 раза дальше от Солнца, чем наша Земля. Следовательно, если известно время обращения какой-нибудь планеты, то по нему можно найти её среднее расстояние от Солнца. Таким путём Кеплеру удалось определить расстояния всех известных в ту пору планет:

Только это были относительные расстояния – числа, показывающие, во сколько раз та или иная планета дальше от Солнца или ближе к Солнцу, чем Земля. Истинные значения этих расстояний, выраженные в земных мерах (в км), оставались неизвестными, ибо ещё не была известна длина астрономической единицы – среднего расстояния Земли от Солнца.

Третий закон Кеплера связал в единую стройную систему всё солнечное семейство. На поиски ушло девять трудных лет. Победило упорство учёного!

Вывод: законы Кеплера теоретически развивали гелиоцентрическое учение и тем самым укрепляли позиции новой астрономии. Астрономия Коперника – самое мудрое из всех произведений человеческого ума. [1]

Последующие наблюдения показали, что законы Кеплера применимы не только для планет Солнечной системы и их спутников, но и для звёзд, физически связанных между собой и обращающихся вокруг общего центра масс. Они легли в основу практической космонавтики, ибо по законам Кеплера движутся все искусственные небесные тела, начиная с первого советского спутника и кончая современными космическими аппаратами. Не случайно в истории астрономии Иоганна Кеплера называют «законодателем неба».

Источник

Закон Кеплера

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Форма Земли

Сейчас нам сложно представить, что раньше люди верили, будто Земля плоская. У греков, например, плоскость просто парила в воздухе и была окружена ледниками. А в Индии верили, что планета покоится на трех слонах, которые стоят на черепахе. Впрочем, кое-кто до сих пор так думает. Доказательств того, что наша планета на самом деле не плоская — много, но вот вам парочка, чтобы можно было поддержать светскую беседу.

Гравитация

Гравитация всегда притягивает все в сторону центра масс. Наша Земля — сферической формы, а центр масс сферы находится как раз в ее центре.

Гравитация притягивает все объекты на поверхности в направлении ядра Земли, то есть вниз, независимо от их местоположения — что мы всегда и наблюдаем.

Если представить, что Земля плоская, то гравитация должна будет притягивать все, что на поверхности, к центру плоскости. То есть если вы окажетесь у края плоской Земли, гравитация будет тянуть вас не вниз, а к центру диска.

Чтобы доказать свою точку зрения, сторонникам плоской Земли придется поискать на планете место, где вещи падают не вниз, а вбок.

Если бы Земля была плоской, да еще и со слонами и черепахой, то при лунном затмении мы бы видели не равномерно растущую тень, а примерно такую картину:

Но, пожалуй, это сильно отличается от реальности.

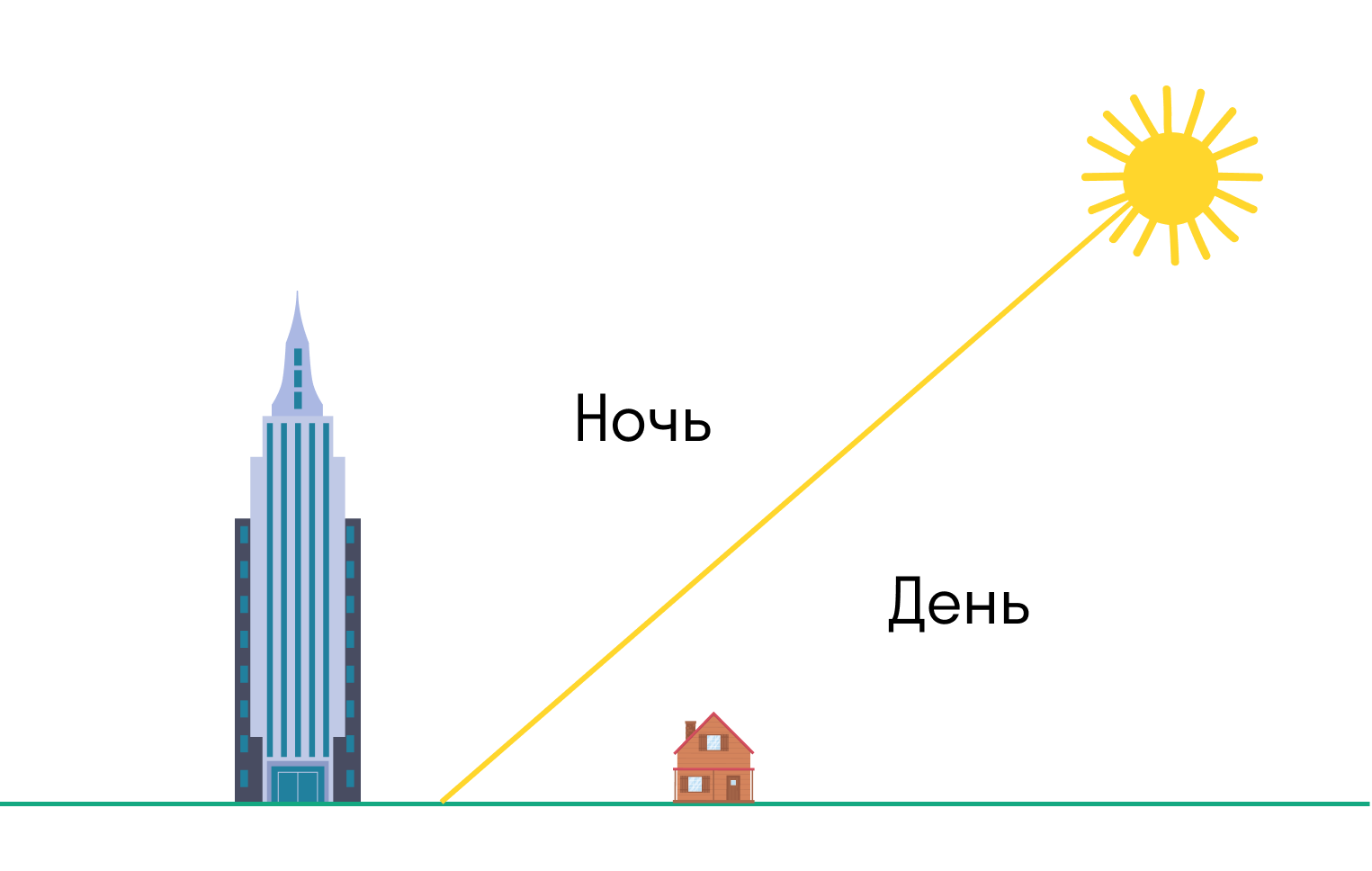
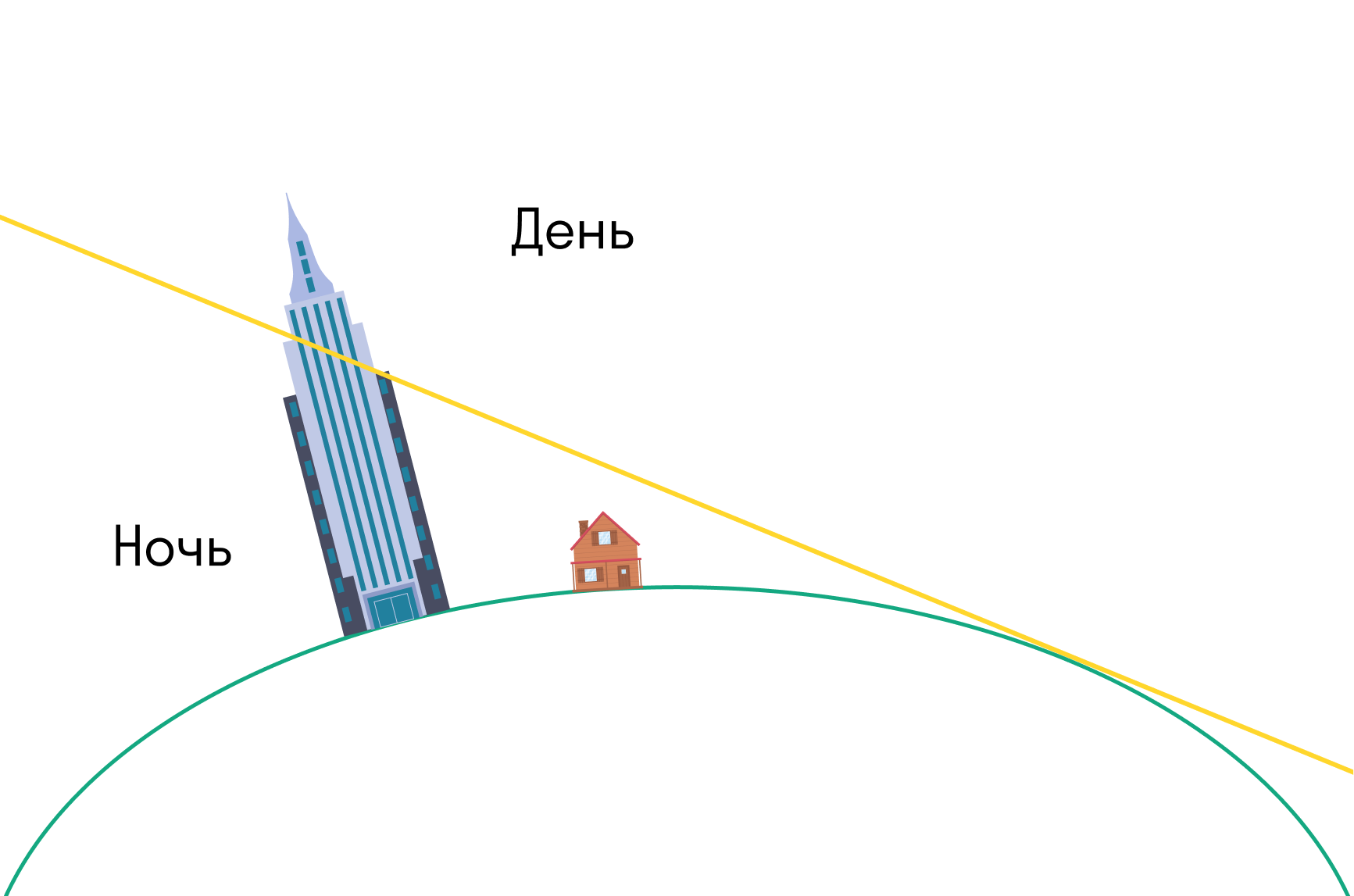
На плоскую Землю свет от Солнца падал бы, как свет от фонаря. То есть высокие объекты в противоположном от Солнца направлении после заката оставались бы в тени.

А на шарообразной Земле небоскребы или горы будут освещены Солнцем после заката или перед рассветом.

Именно это вы увидите, если застанете рассвет или закат в горах — или посмотрите на фотографии.

Окей, Земля все-таки не плоская — с этим разобрались. Но и шаром ее назвать нельзя: Земля имеет форму эллипсоида.

Эллипсоид — это такой приплюснутый шар, в сечении у которого эллипс. Именно по траектории эллипса вращаются все спутники.

Эллипс

Эллипс — это замкнутая прямая на плоскости, частный случай овала. У эллипса две оси симметрии — горизонтальная и вертикальная, которые состоят из двух полуосей.

А еще у эллипса два фокуса — это такие точки, сумма расстояний от которых до любой точки P(x,y) является постоянной величиной.

Эллипс

F₁ и F₂ — фокусы

с — половина расстояния между F₁ и F₂

a — большая полуось

b — малая полуось

r₁ и r₂ — фокальные радиусы

Теперь мы знаем все необходимые понятия, чтобы разобраться, в чем состоят законы Кеплера.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Первый закон Кеплера

Каждая планета солнечной системы вращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка B траектории называется перигелием, а точка A, наиболее удаленная от Солнца — афелием.

Первый закон Кеплера достаточно простой, но важный, так как в свое время он сильно продвинул астрономию. До этого открытия астрономы считали, что планеты движутся исключительно по круговым орбитам. Если же наблюдения противоречили этому убеждению, ученые дополняли главное круговое движение малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Кеплер получил доступ к огромной базе наблюдений Тихо Браге и, изучив их, перешагнул старые идеи.

Второй закон Кеплера (закон площадей)

Радиус-вектор планеты описывает в равные промежутки времени равные площади.

Каждая планета перемещается в плоскости, проходящей через центр Солнца. В одно и то же время радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную.

На практике это можно заметить по движению Земли. Ежегодно в начале января наша планета проходит через перигелий и перемещается быстрее. Из-за этого движение Солнца по эклиптике также происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее. Поэтому световой день летом длиннее, чем зимой.

Третий закон Кеплера

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и средним расстоянием от Солнца до планеты или спутника устанавливается связь. Этот закон выполняется как для планет, так и для спутников с погрешно­стью менее 1%.

Третий закон Кеплера

T₁ и T₂ — периоды обращения двух планет [c]

a₁ и a₂ — большие полуоси орбит планет [м]

На основании этого закона можно вычис­лить продолжительность года (времени полного оборота вокруг Солнца) любой планеты, если известно ее расстояние до Солнца.

Также можно проделать обратное — рассчитать орбиту, зная период обращения.

Закон всемирного тяготения

Законы Кеплера — это результаты наблюдений и обобщений. Теоретически их обосновал Исаак Ньютон в законе всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником нашей планеты.

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него это получалось, аппарат должен иметь начальную скорость, которая равна или больше первой космической.

Первая космическая скорость

v₁ — первая космическая скорость [м/с]

g — ускорение свободного падения на данной планете [м/с 2 ]

R — радиус планеты [м]

Есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Вторая космическая скорость

v₂ — вторая космическая скорость [м/с]

g — ускорение свободного падения на данной планете [м/с 2 ]

Источник

Законы Кеплера

В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.

Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.

Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.

С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (

140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.

Рисунок 1.24.1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд

Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном Иоганн Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Тихо Браге.

Первый закон Кеплера (1609 г.):

Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.

Рисунок 1.24.2. Эллиптическая орбита планеты массой m –11 Н·м 2 /кг 2 – гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, уже говорилось, что сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу. Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2 Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки. Потенциальная энергия тела массы m, находящегося на расстоянии r от неподвижного тела массы M, равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность. Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5). Рисунок 1.24.5. Вычисление потенциальной энергии тела в гравитационном поле Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. 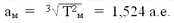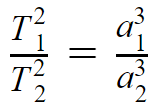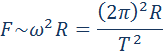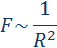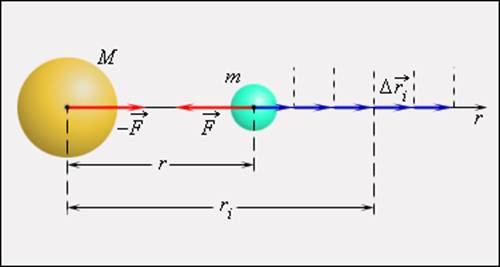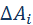Работа гравитационной силы 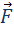на малом перемещении 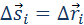есть: Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ ΔAi на малых перемещениях: В пределе при Δri → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение Знак «минус» указывает на то, что гравитационные силы являются силами притяжения. Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ, его полная механическая энергия равна В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной. Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6). При E = E1 rmax. В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы). Рисунок 1.24.6. Диаграмма энергий тела массой m в гравитационном поле, создаваемом сферически симметричным телом массой M и радиусом R При E = E2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории. При E = E3 > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии. Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля. Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли. Эту скорость необходимо набрать, чтобы преодолеть притяжение Земли и вывести тело (например, спутник) на орбиту Земли. Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории. Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·10 3 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·10 3 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе. Источник ← постеры япония на стену Общие средства office что это за программа → Вам также понравится Один наушник упал в воду что делать 14.10.202323.08.2023 admin 0 помещение под полом подвал 12.10.202316.08.2023 admin 0 поле источник в битрикс24 17.10.202315.08.2023 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email *