Нулевой вектор коллинеарен чему
Что такое вектор
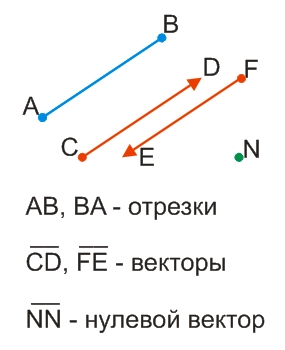
Направленный отрезок называется вектором.
Отрезок называется направленным, если у него указаны начало и конец, т.е., указано направление.
О том, что данный отрезок является вектором, говорит горизонтальная черта над буквами, обозначающими вектор.
Условия равенства векторов:
Длиной вектора или модулем вектора называется длина отрезка, обозначающего этот вектор.
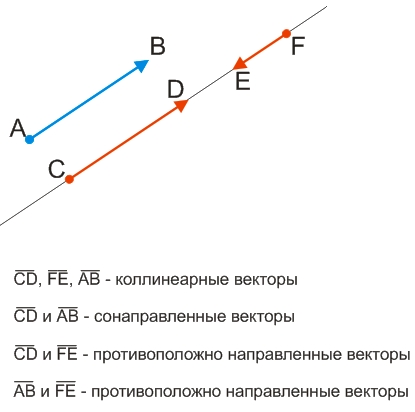
Коллинеарными называются вектора, лежащие на одной и той же прямой или принадлежащие параллельным прямым.
Нулевой вектор считается коллинеарным любому вектору.
Два ненулевых коллинеарных вектора считаются сонаправленными, если их направления совпадают.
Нулевой вектор считается сонаправленным любому вектору.
Два ненулевых коллинеарных вектора считаются противоположно направленными, если их направления противоположны.
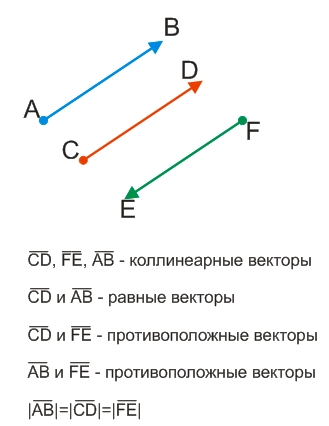
Два сонаправленных вектора считаются равными, если они имеют одинаковую длину (модуль).
Два противоположно направленных вектора, имеющих одинаковые модули, называются противоположными (следует различать противоположно направленные векторы и противоположные векторы).
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Координатная форма условия коллинеарности векторов
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Решение
Ответ: заданные векторы коллинеарны.
Решение
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Решение
Решение
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Коллинеарные вектора
Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).
Содержание
Обозначения
Свойства коллинеарности
Пусть 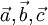

Другие объекты
Выше описанные критерии коллинеарности позволяют определить это понятие для векторов, понимаемых не в геометрическом смысле (а, например, как элементы произвольного линейного пространства).
Иногда коллинеарными называют те точки (или другие объекты), которые лежат на (принадлежат) одной прямой.
См. также
Полезное
Смотреть что такое «Коллинеарные вектора» в других словарях:
Коллинеарные векторы — Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Допустим, но не рекомендуется, синоним «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или… … Википедия
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ — векторы, лежащие на одной прямой или на параллельных прямых. Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. Нулевой вектор коллинеарен всякому вектору. Аналогично,… … Математическая энциклопедия
Коллинеарность — Два коллинеарных противоположно направленных вектора Два ненулевых (не равных 0) вектора называются … Википедия
Вектор — направленный отрезок прямой, или отрезок, один из концов которого называется началом вектора, а другой его концом. Различают: 1) коллинеарные векторы, лежащие на одной прямой или на параллельных прямых; 2) компланарные векторы, лежащие в одной… … Начала современного естествознания
Коллинеарные векторы
В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.
Условия коллинеарности векторов
Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.
Два вектора коллинеарны, если выполняется одно из условий ниже:
2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.
3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).
Примеры задач
Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.
Задание 2
Выясним, при каком значении n векторы и коллинеарны.
Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.