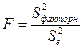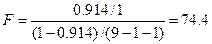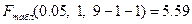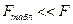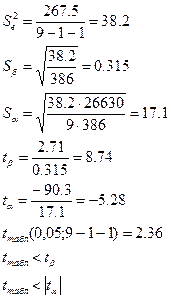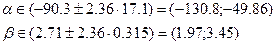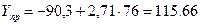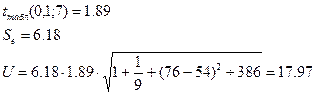Нулевая гипотеза при проверке коэффициента уравнения регрессии на статистическую значимость гласит

Проверка статистической значимости уравнения регрессии и его параметров

а) проверка статистической значимости уравнения:

Проверка значимости (существенности) уравнения регрессии позволяет установить, существенна ли связь включенных в уравнение признаков (Y и X), соответствует ли математическая модель, выражающая зависимость Y и X, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y. Иными словами оценка значимости уравнения регрессии позволяет узнать пригодно ли оно для практического использования (например, для прогнозирования) или нет.

Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера:

или в терминах коэффициента детерминации

,

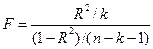
где n – длина совокупностей данных, k – количество факторов, включенных в модель (в уравнении парной регрессии k=1).

Уравнение регрессии статистически значимо, если

.

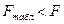
1) определяется максимальной величиной отношения дисперсий , которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы (нулевая гипотеза о незначимости уравнения в целом);

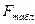
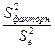
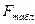
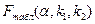
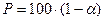
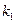
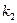
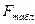
2) для определения можно использовать статистическую функцию FРАСПОБР, предварительно задав три параметра , где – заданный уровень значимости проверки или уровень вероятности ( связано с вероятностью Р формулой ); – число степеней свободы числителя, равное количеству k факторов, включенных в модель; – число степеней свободы знаменателя (n-k-1). Таким образом, зависит от заданной вероятности, числа уровней в совокупностях данных и вида уравнения регрессии.

Пример (продолжение).

4) Проверить значимость уравнения регрессии с помощью F-критерия Фишера ( =0,05)

вывод: уравнение регрессии статистически значимо, связь включенных в него признаков существенна;

Значение F-критерия можно получить также в таблице «Дисперсионный анализ» отчета по работе с инструментом регрессия (рис. 13).

Рис. 13. Фрагмент регрессионного анализа

а) проверка статистической значимости параметров уравнения:

В линейной регрессии обычно оценивается значимость не только уравнения регрессии, но и отдельных его параметров. Для этого применяется t-критерий Стьюдента:

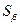
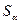
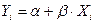
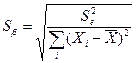
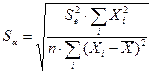
1) рассчитывают стандартные ошибки (среднеквадратические отклонения) и каждого из параметров уравнения по формулам

, ,

где 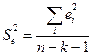–остаточная дисперсия, k – число факторов в уравнении регрессии (в нашем случае k=1);

2) определяют расчетные значения t-критерия Стьюдента:

, ;

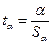
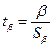
3) определяют табличное значение t-критерия 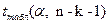с помощью статистической функции СТЬЮДРАСПОБР по двум параметрам: заданному уровню значимости и одной степени свободы (n-k-1);

4) параметры уравнения регрессии будут статистически значимы, если выполняются неравенства:

, .

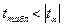
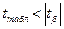
Замечания:

1) статистическая значимость (незначимость) коэффициента регрессии 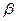означает одновременно статистическую значимость (незначимость) фактора Х, включенного в уравнение; статистически незначимый (или несущественный) фактор должен быть устранен из модели или заменен другим;

2) статистическая значимость (незначимость) параметра уравнения означает верную (неверную) спецификацию модели; под спецификацией понимают:

а) выбор вида уравнения;

б) определение независимых факторов для включения в модель;

3) t-критерий можно использовать также для определения интервальных оценок параметров модели:

,

.

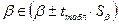
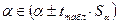
Поскольку коэффициент регрессии 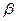в эконометрических исследованиях имеет четкую экономическую интерпретацию, доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, то есть не должны содержать одновременно положительные и отрицательные величины и даже нуль.

Пример (продолжение).

4) осуществить проверку значимости параметров уравнения регрессии по t-критерию Стьюдента ( =0,05)

Вывод: оба параметра модели статистически значимы.

Дополнение: интервальные оценки параметров

Расчетные значения t-критерия, а также интервальные оценки параметров можно найти в отчете по результатам работы с инструментом Регрессия (рис. 14).

Рис. 14. Фрагмент регрессионного анализа

2.4. Экономический прогноз

Рассматриваемая модель 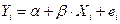может быть использована для определения прогнозных оценок исследуемой величины. При прогнозировании на основе регрессионных моделей можно выделить три основных этапа:

1) точечный прогноз фактора Х;

2) точечный прогноз показателя Y;

3) интервальный прогноз показателя Y.

Рассмотрим содержание этих этапов подробнее.

1) точечный прогноз фактора Хв зависимости от специфики исходных данных и условия задачи можно определить одним из следующих способов:

а) если исходные данные являются временными рядами, то для прогноза фактора можно воспользоваться методами экстраполяции и использовать наиболее подходящую модель временного ряда

.

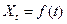
Тогда прогноз фактора на k шагов вперед определяется по формуле

.

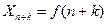
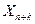
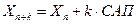
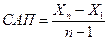
б)вслучае временных рядов можно найти также с помощью среднего абсолютного прироста (САП) по формуле

, .

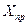
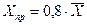
в)если исходные данные являются пространственными, то, очевидно, в задаче будет задано правило для определения . Например, если прогнозное значение фактора составляет 80 % от его среднего значения, то .

2) точечный прогноз показателя Yнаходят подстановкой в модель прогнозных значений фактора:

– в случае пространственных данных,

– в случае временных рядов.

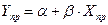
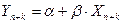
3) интервальный прогноз показателя Y:

вначале находят ошибку прогнозирования

,

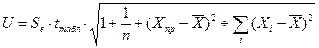
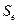
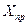
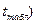
которая зависит от стандартной ошибки модели , удаления от своего среднего значения, количества наблюдений n, заданного уровня вероятности попадания в интервал прогноза (он определяет величину ;

затем находят сам доверительный интервал прогноза:

нижняя граница интервала – ,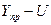

верхняя граница интервала – .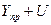

Пример (продолжение).

5) осуществить прогнозирование среднего значения показателя Y при уровне значимости =0,1, если прогнозное значение фактора Х составит 117 % от его максимального значения

1) точечный прогноз фактора Х

,

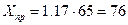
2) точечный прогноз показателя Y

3) интервальный прогноз показателя Y

Нижняя граница интервала: 115,66-17,97=97,69

Верхняя граница интервала: 115,66+17,97=133,63.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Нулевая гипотеза при проверке коэффициента уравнения регрессии на статистическую значимость гласит что

Коэффициенты регрессии, как и коэффициенты корреляции, — случайные величины, зависящие от объема выборки. Поэтому для проверки надежности коэффициента регрессии выдвигается гипотеза о том, что коэффициент регрессии в генеральной совокупности равен нулю (нулевая гипотеза), т. е. связь, установленная по данным выборки, в генеральной совокупности отсутствует. Простейшая схема проверки этой гипотезы при линейной форме связи сводится к построению доверительного интервала для каждого коэффициента регрессии. Если граничные значения данного коэффициента регрессии в этом интервале имеют противоположные знаки, то принятая гипотеза подтверждается и тогда соответствующий этому параметру уравнения фактор исключается из модели. Для нелинейной формы связи имеются другие методы оценки значимости факторов [c.18]

Для проверки этих гипотез нужно определить /-критерий для соответствующего коэффициента регрессии. Эти /-критерии рассчитывают делением коэффициентов регрессии на их стандартные ошибки [c.275]

В методике изложены общие положения описаны вычислительный метод получения оценок коэффициентов регрессии, алгоритм вычисления вектора оценок коэффициентов регрессии, обобщенная обратная матрица и остаточная сумма квадратов отклонений, алгоритм проверки гипотез об отличии коэффициентов регрессии от нуля, оценивания дисперсии оценок коэффициентов регрессии. [c.27]

Если при решении той или иной задачи можно ограничиться линейным приближением, то полный факторный эксперимент типа 2 также оказывается недостаточно эффективным, особенно при большом k. При линейном росте числа независимых переменных число опытов для полного факторного эксперимента растет по показательной функции, в результате слишком много степеней свободы остается на проверку гипотезы адекватности. Например, при k = 2, при линейном приближении, для проверки гипотезы адекватности используется только одна степень свободы, тогда как при k = fj — уже 57 степеней свободы. Правда, при постановке таких больших экспериментов резко снижается ошибка в определении коэффициентов регрессии, так как при факторном планировании все опыты используются для оценки каждого из коэффициентов регрессии. Но это обстоятельство далеко не всегда является достаточным основанием для постановки большого числа опытов. Часто, особенно на первых этапах исследования, бывает нужно получить некоторую, хотя бы и не очень точную, информацию о процессе при минимальной затрате труда на проведение экспериментов. Если можно ограничиться линейным приближением, то число опытов можно резко снизить, используя для планирования так называемые дробные реплики от полного факторного эксперимента [1]. [c.215]

Эмпирическое уравнение регрессии определяется на основе конечного числа статистических данных. Поэтому коэффициенты эмпирического уравнения регрессии являются случайными величинами, изменяющимися от выборки к выборке. При проведении статистического анализа перед исследователем зачастую возникает необходимость сравнения эмпирических коэффициентов регрессии bo и bi с некоторыми теоретически ожидаемыми значениями р0 и pi этих коэффициентов. Данный анализ осуществляется по схеме статистической проверки гипотез, которая подробно проанализирована в разделе 3.4. Для проверки гипотезы [c.120]

Другим важным направлением использования статистики Фишера является проверка гипотезы о равенстве нулю не всех коэффициентов регрессии одновременно, а только некоторой части этих коэффициентов. Данное использование статистики F позволяет оценить обоснованность исключения или добавления в уравнение регрессии некоторых наборов объясняющих переменных, что особенно важно при совершенствовании линейной регрессионной модели. [c.159]

Увеличение дисперсии оценок может привести к ошибочным результатам проверки гипотез относительно значений коэффициентов регрессии, расширению интервальных оценок. [c.195]

Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве нулю части этих коэффициентов. Это особенно важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных, или же, наоборот, включения их в это число. [c.318]

По таблице распределения Фишера с (2 57) степенями свободы находим, что критическое значение Нравно 3,16 при 5 %-ном уровне значимости и 5,0 при 1 %-ном. Таким образом, гипотеза о равенстве нулю одновременно всех коэффициентов регрессии заведомо отвергается (что, впрочем, ясно и из того, что коэффициент при GNP уже до этого получился значимым). Итак, даже небольшая величина /Р = 0,29 при довольно большом числе наблюдений дала значимую величину F-статистики. В то же время если величина R2 рассматривается как самостоятельный критерий качества регрессии (а не только как средство проверки нулевой гипотезы для всех коэффициентов одновременно), позволяющий оценить его в сравнении с качеством линии у = у, то значение R2 = 0,29 вряд ли можно считать хорошим. Это говорит о необходимости дальнейшего поиска объясняющих переменных для показателя RNX. [c.337]

Статистические свойства МНК-оценок параметров регрессии. Проверка гипотезы b = bo. Доверительные интервалы для коэффициентов регрессии [c.46]

Если регрессия оказывается значимой, то можно продолжить анализ, используя t-тесты для отдельных коэффициентов регрессии в этом случае пытаются выяснить, насколько значимой является влияние той или иной переменной j на параметр у при условии, что все другие факторы Xk остаются неизменными. Построение доверительных интервалов и проверка гипотез на адекватность для отдельного коэффициента регрессии основывается на определении стандартной ошибки. Каждый коэффициент регрессии имеет свою стандартную ошибку Sb, Sb2. Sbk. [c.55]

Проверка значимости включает проверку значимости общего уравнения регрессии и конкретных частных коэффициентов регрессии, гипотеза для проверки общего уравнения гласит, что коэффициент множественной детерминации для генеральной совокупности равен нулю [c.664]

Если нулевую гипотезу отклоняют, то один или несколько частных коэффициентов регрессии в совокупности имеют значение, отличное от нуля. Чтобы определить, какие из конкретных коэффициентов Отличны от нуля, выполним дополнительные проверки. Проверку значимости Д выполним тем же способом, что и в случае парной регрессии, т.е. используя г статистику. Значимость частного коэффициента для переменной — погодные условия — можно выполнить с помощью уравнения 0.5887 [c.664]

Рассмотренные направления проверки статистических гипотез охватывают лишь важнейшие из них. Процедура испытания статистических гипотез применяется для определения того, случайно или нет полученное значение коэффициента корреляции, коэффициента вариации и т. д., случайны или нет различия в значениях показателей (медиан, коэффициентов корреляции, регрессии и т.д.) в разных [c.217]

Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. Для коэффициента парной регрессии Ь средняя ошибка оценки вычисляется как [c.247]

При анализе временных рядов часто приходится учитывать статистическую зависимость наблюдений в разные моменты времени. Иными словами, для многих временных рядов предположение о некоррелированности ошибок не выполняется. В этом разделе мы рассмотрим наиболее простую модель, в которой ошибки образуют так называемый авторегрессионный процесс первого порядка (точное определение будет дано ниже). Как было показано ранее (глава 5), применение обычного метода наименьших квадратов к этой системе дает несмещенные и состоятельные оценки параметров, однако можно показать (см., например, Johnston and DiNar-do, 1997), что получаемая при этом оценка дисперсии оказывается смещенной вниз, что может отрицательно сказаться при проверке гипотез о значимости коэффициентов. Образно говоря, МНК рисует более оптимистичную картину регрессии, чем есть на самом деле. [c.184]

Для проверки существования AR H необходимо возвести в квадрат ошибки из первоначального уравнения условной средней. Этот ряд квадратов регрессируется по константе и прошлым значениям квадратов с лагом р. Критерием является Т R2, где Т — размер выборки и R2 — коэффициент множественной регрессии из уравнения регрессии квадратов ошибок. Этот критерий подчиняется х2 РаспРеДелению. Число степеней свободы равно числу временных лагов в регрессии. Если значение критерия больше критического значения из таблиц х2, то нулевая гипотеза о том, что AR H не присутствует, отвергается. [c.356]

Необходимо несколько более подробно остановиться на методике эмпирической проверки концепций конвергенции. Наиболее часто используемым статистическим методом для проверки абсолютной Дконвергенции является регрессия темпа роста ВВП, среднего или накопленного за рассматриваемый период, на константу и логарифм начального ВВП на душу населения (на основе одномоментного среза межобъектных данных). Если коэффициент при объясняющей переменной статистически значим и имеет отрицательный знак, гипотеза абсолютной Дконвергенции не отвергается. [c.36]

Источник