Нормальное распределение интеллекта означает что показатели близкие к
Нормальное распределение интеллекта означает что показатели близкие к
Измеримые физиологические показатели, например артериальное давление, концентрация холестерина сыворотки или индекс массы тела, варьирующие у разных индивидуумов, — важные показатели здоровья и болезней в популяции. Такие изменения обычно вызваны различиями в генотипе, а также негенетическими факторами (т.е. окружающей средой).
Задача генетика — определить степень влияния генов на такую изменчивость, идентифицировать эти гены и выявить ответственные аллели.
Нормальное (Гауссово) распределение физиологического показателя
Как часто случается с физиологическими показателями, измеренными в популяции, график числа индивидуумов в популяции (ось Y), имеющих конкретный количественный показатель (ось X), формирует колоколообразную кривую, известную как кривая нормального (Гауссова) распределения.
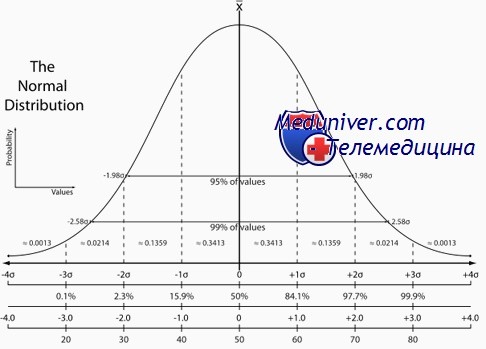
В графике популяционной частоты с нормально распределенными величинами положение вершины графика и его форма полностью определяются двумя значениями — средним (u) и дисперсией (а2) соответственно. Среднее — это простое среднее арифметическое величин, и поскольку больше людей имеет величины признака около среднего значения, кривая имеет пик в этой точке.
Дисперсия (или ее квадратный корень, среднеквадратичное отклонение, о) — мера разброса значений в обе стороны от среднего, и, следовательно, определяет ширину кривой. Любой физиологический показатель, который может быть измерен, представляет количественный фенотип, со своим средним и дисперсией. Изменчивость показателя в популяции называют общей фенотипической изменчивостью.
Нормальный диапазон физиологического показателя
Нормальный диапазон физиологического показателя — одно из фундаментальных понятий в клинической медицине. Например, чрезвычайно высокий или низкий рост, артериальную гипертонию, гиперхолестеринемию и ожирение считают аномальными, когда их величина выходит за пределы нормального диапазона. При оценке здоровья детей рост, масса тела, окружность головы и другие размеры сравнивают с «нормальным» размером для ребенка такого пола и возраста.
Однако как определить диапазон нормы? Во многих ситуациях в медицине конкретная измеренная физиологическая величина «нормальна» или «аномальна» в зависимости от того, насколько значительно она отличается от среднего. Нормальная форма распределения определяет границы диапазона нормы.
Статистическая теория утверждает, что когда количественный признак встречается в популяции в соответствии с законом нормального распределения, только 5% популяции имеет значения показателя, выходящие за 2 среднеквадратичных отклонения выше или ниже популяционной средней. (Обратите внимание, что слово «нормальное» использовано здесь в двух разных значениях — что физиологический показатель имеет нормальную форму распределения в популяции и что индивидуальная величина находится в пределах диапазона нормы.)
Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021
Нормальное распределение интеллекта означает что показатели близкие к
Приложение теории Гаусса в социологии
Ограниченность недалеких людей компенсируется неограниченностью их количества.
В различных областях науки широко применяется так называемая кривая Гаусса (гауссиана), по имени Иоганна Карла Фридриха Гаусса – великого физика, математика и астронома. В свое время он сформулировал закон нормального распределения, в соответствии с которым любая физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех.
КРИВАЯ ГАУССА
Откуда взялась теория Гаусса?
Великий Иоганн Карл Фридрих Гаусс проводил опыты по капанию из пипетки, закрепленной на штативе. В одно и то же место капли не попадали. Решил, что стол качается, подложил под ножку деревяшку. Не попадают в одно место. Решил, что ветер дует, закрыл окно, дверь, подложил тряпку под дверь. Все равно разброс. Задернул шторы, выключил свет. Опять не попадает. Тогда он бросил физику и создал «Теорию ошибок», или, как говорят физики, «погрешностей», которая сейчас является частью высшей математики, в частности теории вероятности и теории сложных систем.
Большинство совокупных погрешностей (ошибок) в природе и обществе подчиняется закону нормального распределения Гаусса. Этот закон нормального распределения и представляет собой кривую Гаусса (нормальное эмпирическое статистическое распределение), графическое изображение которого напоминает колокол (bell curve), на вершине которого покоятся наиболее часто встречающиеся значения. Чем ближе к краям, тем значение ниже.
В соответствии с теорией Гаусса, заметные отклонения встречаются значительно реже, чем средние величины. Закон начинает действовать в группе при условии: чем больше элементов, тем нагляднее проявляется «нормальное распределение» – шире разброс крайних значений и более выражен горб середины.
Когда оказалось, что такая ситуация крайне широко распространена в природе и обществе, кривая Гаусса нашла широкое распространение при исследовании свойств личности человека в социологии и может быть применена, например, для характеристики живых организмов в популяции.
В том числе, распределение умных людей в обществе подчиняется закону нормального распределения Гаусса, и, по его теории, большинство населения, к сожалению, неумно.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ИНТЕЛЛЕКТА
Еще Станиславский отмечал: «Гении родятся веками, большие таланты – десятилетиями, таланты – годами, посредственности – днями и бездарности – часами». А Бернард Шоу достаточно математично утверждал, что «2 процента людей – думает, 3 процента – думает, что они думают, а 95 процентов людей лучше умрут, чем будут думать».
В упрощенной форме это правило звучит: «Трое умнее, чем пятеро»[66], что созвучно с древней истиной «худших всегда большинство».
Это распределение работает в любых человеческих коллективах.
Даже среди чернорабочих всегда найдется человек, знающий философию или высшую математику. Он будет только один на 30–40 человек, но он будет обязательно.
И, соответственно, в любом, даже самом умном сообществе найдется и явно неумный человек.
Даже на юридическом факультете МГУ из 100 преподавателей найдется 6 явно недостаточно умных. Например, когда в 1996 году профессор Зенин читал на вечернем отделении гражданское право, он просто брал в руки Гражданский кодекс и читал его вслух. И так всю лекцию, не вставив ни одного своего слова. Пока курс не собрал подписи на его замену. Тогда его заменили на профессора Мартьянову, которая явно относится к противоположной части шкалы. Сильная, принципиальная и очень умная женщина.
Однако в 2015 г. профессор Зенин продолжает читать на вечернем отделении гражданское право тем же самым методом, что еще раз подчеркивает правоту использования «гауссова распределения» в оценке интеллектуального уровня в любых коллективах.
Умный человек как мутация, ошибка природы
Но при внимательном исследовании кривой Гаусса можно сделать вывод не только о количестве умных и неумных людей в обществе.
Если руководствоваться не только кривой нормального распределения, но и вытекающей из нее теорией сложных систем, в сильно упрощенном виде гласящей, что: «любая сложная система, состоящая из достаточно большого числа достаточно сложных элементов, соединенных достаточно большим числом достаточно сложных нелинейных и, в том числе, обратных связей, обязательно содержит ошибку», можно прийти к выводу, что любой умный человек является ошибкой природы, отклонением от «нормы».