Неверно что иванов и петров оба не выдержали экзамен
Индивидуальное задание. 1. Установите, какие из предложений являются логическими высказываниями, а какие – нет (объясните почему)
1. Установите, какие из предложений являются логическими высказываниями, а какие – нет (объясните почему), сформулируйте отрицания:
1.1 «Солнце есть спутник Земли»;
1.2 «2+3=4»;
1.3 «Сегодня отличная погода»;
1.4 «В романе Л. Н. Толстого “Война и мир” 3 432 536 слов»;
1.5 «Санкт-Петербург расположен на Неве»;
1.6 «Музыка Баха слишком сложна»;
1.7 «Первая космическая скорость равна 7.8 км/сек»;
1.8 «Железо – металл»;
1.9«Если один угол в треугольнике прямой, то треугольник будет тупоугольным»;
1.10 «Иван Петров плотник»;
1.11«Студент учатся в институте»;
1.12«Треугольник – плоская геометрическая фигура, состоящая из трех углов и трех сторон»;
1.13«Каждый квадрат есть ромб»;
1.14«Курица не птица»;
1.15«Математика – это наука».
2.Запишите предложение формулой логики высказываний, постройте к нему отрицание:
2.1 Неверно, что Иванов и Петров оба не выдержали экзамена.
2.2 Если Коля умен, а Вася нет, то Коля получит аттестат с отличием.
2.3 Если в классе идут занятия, то на улице хорошая погода.
2.4 Валя ходит в кино только в том случае, когда там показывают комедию.
2.5 Треугольники подобны, если они равны.
2.6 Противоположные стороны параллелограмма равны и параллельны, в противном случае четырехугольник не параллелограмм, а трапеция.
2.7Неверно, что у ромба все углы острые и диагонали не перпендикулярны.
2.8 Или Катя пойдет в кино, а Сергей не пойдет, или они оба пойдут в школу.
2.9 Если курс ценных бумаг растет или процентная ставка снижается, то либо падает курс акций, либо налоги не повышаются.
2.11«Сумма цифр числа 216 делится на 3, значит само число 216 делится на 3, так как существует соответствующее правило»;
2.13«Я понимаю, что не понимаю математическую логику, поэтому мне необходимо дополнительно заниматься дома»;
2.14«Если Иван Иванович Иванов не будет ходить на работу, то он или не получит зарплату, или будет уволен»;
2.15«Максим учится в школе, и делает уроки старательно, это значит, что он отличник».
Таблицы истинности
Истинность высказывания можно установить с помощью таблицы истинности. Таблица истинности – это таблица, состоящая из нулей и единиц и устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции.
Таблицы истинности применяются для:
· вычисления истинности сложных высказываний;
· установления эквивалентности высказываний;
1. Таблица истинности инверсии:
| A | 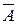 |
2. Таблица истинности дизъюнкции:
| A | B | А 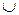 В В |
3. Таблица истинности конъюнкции:
4. Таблица истинности импликации:
5. Таблица истинности эквиваленции:
6. Таблица истинности строгой дизъюнкции:
Высказывание «Eсли я куплю яблоки или абрикосы, то приготовлю фруктовый пирог» формализуется в виде 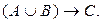
Формула 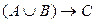
Некоторые формулы принимают значение «истина» при любых значениях истинности входящих в них переменных и называются тождественно истинными формулами или тавтологиями.
Высказывание «Катя самая высокая девочка в классе, и в классе есть девочки выше Кати» формализуется в виде: 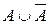
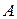
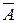
Такие формулы называются тождественно ложными формулами или противоречиями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом «=» или « 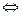
Пример 1.Установить истинность высказывания 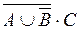
В состав сложного высказывания входят простые: А, В, С. В таблице заполняются колонки значениями (0, 1). Указываются все возможные ситуации. При составлении таблицы надо следить за тем, чтобы не перепутать порядок действий; заполняя столбцы, следует двигаться от элементарных формул к более сложным; столбец, заполняемый последним, содержит значения исходной формулы.
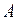 | 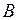 | 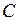 | 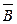 | 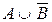 | 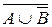 | 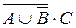 |
Из таблицы видно, что данное высказывание истинно только в случае, когда А=0, В=1, С=1. Во всех остальных случаях оно ложно.
С помощью таблиц истинности можно установить эквивалентность двух или нескольких высказываний.
Высказывания называются эквивалентными, если соответствующие значения каждого из них совпадают в таблице истинности.
Пример 2. Проверить эквивалентность высказываний 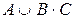
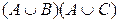
Проверка ведется путем составления таблицы истинности:
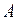 | 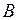 | 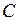 | 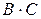 | 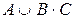 | 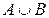 | 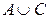 | 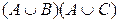 |
Сравнивая 5-ю и 8-ю колонки, убеждаемся, что все значения, получаемые по формуле 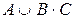
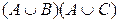
Эквивалентные (равносильные) высказывания соединяют знаком «↔» («≡», «
», « 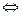
Пример 3. Докажите тавтологию 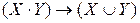
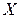 | 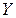 | 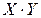 | 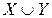 | 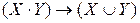 |
Так как высказывание всегда истинно, то оно является тавтологией.
Пример 4. Докажите тавтологию ((X→Y)→(Y→Z))→(X→Z).
Решение:
_ _ _ _ _ _ _ _ _ _ _ _ _ F1 _ _ _ _ F2 _ _ _ _ _ F3
| X | Y | Z | X→Y | Y→Z | X→Z | F1→F2 | (F1→F2) →F3 |
Из таблицы видно, что исследуемое высказывание – тавтология, так как оно тождественно истинно.
Упражнения
1.Установить, какому из высказываний эквивалентно высказывание 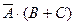
а) 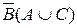
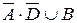
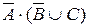
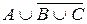
2. Установить с помощью таблиц истинности, какие из следующих формул являются тавтологиями:
а) 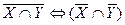
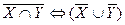
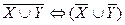
г) 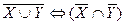
3. Установить истинность высказывания 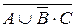
4. Проверить эквивалентность высказываний 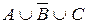
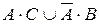
5. Установить, являются ли высказывания тавтологиями:
а) 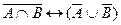
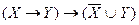
6. Для каждой формулы придумайте формализуемые ими предложения:
а) 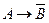
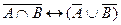
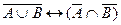
7. Из простых высказываний: «Виктор хороший пловец» – А, «Виктор хорошо ныряет» – В, «Виктор хорошо поет» – С, составлено сложное высказывание 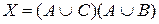
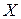
8. Установить истинность высказываний:
а) 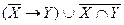
б) 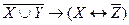
9. Установить истинность высказываний:
а) 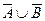
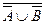
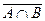
б) 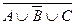
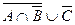
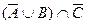
в) 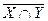
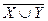
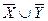
г) 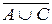
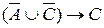
Элементы логики предикатов (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Ú-удаление соответствует разбору случаев. Если в некоторой ситуации из AÚB нужно вывести C, то мы рассуждаем так: если верно AÚB, то либо A, либо B, и поэтому достаточно разобрать случаи, вывести C из A и вывести C из B по отдельности;


Правило Ø-введения соответствует рассуждению от противного, приведению к абсурду (традиционное латинское название – reductio ad absurdum): чтобы установить ØA, достаточно, допустив A, получить противоречие, т. е. вывести B и ØB одновременно для подходящего B.
Руководствуясь этими идеями, можно доказывать выводимость логических законов, исходя из их содержательного смысла. Разумеется, в технике естественного вывода можно использовать и другие секвенции, выводимости которых уже установлены, или иные допустимые правила.
Еще одно полезное правило – правило подстановки:
Г
Примеры
Построить вывод в ИП для формулы 


В более традиционной (но менее точной) записи это высказывание имеет вид: 

Решение


это пример схемы аксиом (ип2);
у (

по правилу (Gen) из (а), структурное требование выполняется, так как (а) – не гипотеза (а аксиома ИП);
у (




это пример схемы аксиом (ип12) (существенно, что 


вытекает из (б) и (в) по правилу (MP).
Соответствующее дерево вывода имеет вид:
Пример 3.4
Привести краткое обоснование пяти допустимых структурных правил вывода в ИП).
Решение
Правило 1 – из гипотезы A и ввиду 


Правила 2 – 4 – тривиально допустимы. Вывод, обосновывающий секвенцию выше черты, обосновывает и секвенцию ниже черты;
Правило 5 – из B, A







Доказать логические правила техники естественного вывода в ИП (см. с. 59-60).
Приведем доказательства некоторых из правил (остальные доказываются аналогично).






Ú—введение. Имеем: Г



Ú—удаление. Из данных Г,A















































Доказать в ИП, что 


Согласно 




Начнем с первой секвенции. Слева у нее стоит дизъюнкция, поэтому, разбирая случаи согласно Ú- удалению, достаточно установить два факта:
A



Установим только первый, второй устанавливается симметрично. Для вывода отрицания Ø(ØA







Первая секвенция выводима по закону тождества. Для вывода второй согласно 

Теперь установим: Ø(ØA



Ø(ØA




Первая секвенция, очевидно, выводима по закону тождества. Вторую секвенцию получим по 
Ø(AÚB)

Мы выведем первую секвенцию, вторая выводится симметрично. Используя
Ø- введение, достаточно вывести:
Ø(AÚB),A

Но первая из этих секвенций очевидна, а вторая получается с помощью
Ú-введения из Ø(AÚB),A
Вывести 
Решение
Согласно Ø-удалению достаточно вывести 
Ø-введению допустим, что Ø(AÚØA), и получим противоречие: Ø(AÚØA)

Для вывода первой секвенции (Ø-введение) допустим A и получим противоречие: Ø(AÚØA),A

Первая из этих секвенций очевидна, а вторая получается Ú-введением. Аналогично, для получения секвенции: Ø(AÚØA)


Вывести 



Решение
C этой целью допустим 







A(y), 



Первая секвенция есть закон тождества, а вторая получается 
Доказать 


Расположим доказательство в технике естественного вывода прямым образом, «сверху вниз»:
1) A, ØA, ØB
2) A, ØA, ØB
3) A, ØA
4) A, ØA
5) 



Доказать правило подстановки в технике естественного вывода в ИП.
Решение
Пусть для простоты Г есть список 









Далее, 




По (MP) 


Далее, по 


Задачи
3.2. Являются ли выводами в ИП следующие последовательности:
а) 
б) 


в) 


3.3. Каким требованиям должна удовлетворять формула 
а) 

б) 

3.4. Построить выводы формул:
а) 
б) 
в) 
3.5. Являются ли следующие последовательности формул выводами из Г=


а) 

б) 






3.6. Построить выводы из Г= 
а) 
б) 
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ (КОНТРОЛЬНАЯ РАБОТА)
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ
ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
При выполнении контрольной работы следует строго придерживаться следующих правил.
1. Выбор варианта для контрольной работы осуществляется в соответствии с порядковым номером в списке группы (во избежание недоразумений рекомендуется согласовать номер варианта с преподавателем). В соответствии с номером варианта из каждого задания 1-8 выбирается своя задача.
2. Контрольная работа оформляется в тонкой тетради чернилами любого цвета (кроме красного). Для замечаний рецензента оставляются поля. На обложке тетради указывается шифр академической группы, фамилия, имя, отчество студента, его учебный шифр (серия и номер зачетной книжки), домашний адрес, а также наименование дисциплины.
3. Решения задач следует располагать в порядке следования номеров задач, указанных в задании, сохраняя номера задач и записывая исходные условия.
4. Приступая к выполнению контрольной работы, необходимо изучить соответствующий теоретический материал и ознакомиться с практической частью пособия. Решения задач контрольной работы следует оформлять аккуратно, подробно объясняя ход решения. Текст решений должен быть написан разборчиво, без двухсмысленного написания букв и символов. В конце работы необходимо привести список использованной литературы, указать дату выполнения работы и поставить свою подпись.
5. После получения проверенной, но не зачтенной работы следует исправить в ней отмеченные рецензентом ошибки и недочеты. Работа над ошибками, как правило, делается в той же тетради, что и контрольная работа. При необходимости работу над ошибками допускается выполнять в новой тетради, но при отсылке на повторное рецензирование необходимо приложить тетрадь с первоначальным вариантом решений и предыдущей рецензией.
ВАРИАНТЫ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
Задание 1. Записать следующие высказывания в виде формул логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т. е. таких, которые уже не могут быть построены из каких-либо других высказываний:
1. Пусть неверно, что если Джон – коммунист, то Джон – атеист; тогда Джон – коммунист или атеист,
2. Необходимым, но не достаточным условием сходимости последовательности 
3. Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива.
4. Или Сэм пойдет на вечеринку, и Макс не пойдет на нее; или Сэм не пойдет на вечеринку, и Макс отлично проведет время.
5. Неверно, что ни Петров, ни Сидоров не выдержали экзамен.
6. Неверно, что если Иванов или Петров сдали экзамен, то и Сидоров его сдал.
7. Если в точке x функция f(x) достигает экстремума, то ее производная в этой точке либо равна нулю, либо не существует.
8. Векторное поле является простейшим, если его дивергенция равна нулю, либо его ротор равен нулю, либо равны нулю и дивергенция, и ротор.
9. Для того чтобы число было нечетным, достаточно, чтобы оно было простым, но не наоборот.
10. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перпендикулярны или хотя бы один из них равен нулю.
11. Неверно, что ветер дует тогда и только тогда, когда нет дождя, и светит солнце.
12. Джо получит приз в том и только том случае, если он умен или если Джим глуп.
13. Если Джим глуп, а Джо не удастся получить приз, то или Джо не умен, или Джим не глуп.
14. Планы на воскресенье не выполнены, если студент не закончил типовой расчет или не сходил ни в кино, ни на танцы, ни на пляж.
15. Прямая l, принадлежащая плоскости Р и перпендикулярная прямой n, перпендикулярна проекции m прямой n на плоскость P или самой прямой n.
16. Прямая l, принадлежащая плоскости Р и перпендикулярная проекции m прямой n на плоскость P, перпендикулярна прямой n.
18. Неверно, что и Петров, и Иванов не выдержали экзамена; значит, хотя бы один из них сдал экзамен.
19. Если среднее время ожидания поезда метрополитена равно одной минуте, то поезда идут с интервалом не три, а две минуты.
20. Знал бы прикуп – жил бы в Сочи, и кто не рискует, тот не пьет шампанское; значит, знание прикупа гарантирует регулярное потребление шампанского.
21. Если прибор содержит два независимо работающих предохранителя, то он выходит из строя тогда и только тогда, когда выходят из строя оба предохранителя.
22. Прядильный станок остановится, если оборвется нить хотя бы на одном из трех веретен.
23. Если капиталовложения останутся постоянными, то возрастут правительственные расходы и возникнет безработица; но если правительственные расходы не возрастут, то налоги будут снижены; а если налоги будут снижены и капиталовложения останутся постоянными, то безработица не возникнет.
24. Взятку платят тогда и только тогда, когда услуга оказана, поскольку если сначала заплатить, то услугу можно и не получить.
25. Если завтра я получу стипендию или займу деньги у товарища и если магазин будет открыт, то я завтра куплю фотоаппарат нужной модели, если он будет в продаже.
26. Когда погода плохая, то или падает настроение, или портится самочувствие, и в обоих случаях не хочется работать.
27. Коли взялся за гуж, то не говори, что не дюж, или вкалывай, вкалывай, вкалывай.
28. Параметры задачи определены полностью, если исходные данные однозначны и в ответе нет произвольных постоянных.
29. Все я понимаю, только если спросят, то ответить не смогу и засмущаюсь.
30. Сессия – приятное времяпрепровождение, если весь семестр честно учился, но если в семестре отдыхал, то худшей поры, чем сессия, нет.
Задание 2. Построить таблицу истинности для формулы.
Задание 3. По полученной таблице истинности привести исходную формулу к дизъюнктивной нормальной форме.
Задание 4. Упростить полученную в задании 3 формулу, используя законы алгебры логики.
Задание 5. Доказать с помощью тождественных преобразований равносильность упрощенной формулы (задание 4) и исходной (задание 2).
Задание 6. Построить релейно-контактную схему, соответствующую упрощенной формуле (задание 4).
Задание 7. Составить функциональные схемы на базе электронных логических элементов, реализующие логические функции из заданий 3 и 4.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задание 8. Разбить высказывание на элементарные и записать в виде кванторной формулы логики предикатов, используя наименьшее возможное число предикатов наименьшей местности; указать область определения использованных предикатов; привести формулу к предваренной нормальной форме:
1. Либо каждый любит кого-то, и никто не любит всех, либо некто любит всех и кто-то не любит никого.
2. Сумма любых двух чисел, имеющих различную четность, есть число нечетное.
3. Всякий друг Мартина есть друг Джона, а Питер не есть друг Джона; следовательно, Питер не есть друг всякого друга Мартина.
4. Если все рыбы, кроме акул, добры к детям, то найдутся дети, не любящие акул.
5. Если либо всякий любитель выпивки общителен, либо некий ростовщик честен и не пьет вина, то неверно, что всякий ростовщик общителен.
6. Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
7. Поскольку не все птицы могут летать, то есть птицы, не умеющие плавать.
8. Если все школьники пошли в кино или в театр, то все школьники пошли в кино или некоторые школьники пошли в театр.
9. Иногда встречаются люди с глазами разного цвета, значит, есть кареглазые люди или все люди голубоглазы или сероглазы.
10. Не все кошки серы, поэтому все кошки не серые.
11. Функция не имеет точек разрыва тогда и только тогда, когда функция непрерывна в любой точке области определения.
12. Последовательность не имеет конечного предела (сформулировать определение).
13. Если неверно, что всякое натуральное число четно или всякое натуральное число нечетно, то имеются и четные числа, и нечетные.
14. Ты можешь обманывать кое-кого все время, ты можешь обманывать всех некоторое время, но ты не можешь обманывать всех все время.
15. Поскольку некоторые остроумны, только когда пьяны, то либо всякий остроумный пьян, либо пьяны все, его окружающие.
16. Через две различные точки проходит единственная прямая.
17. Ни один политик не честен, поэтому всякий человек – либо правдив, либо – политик.
18. Два произвольных числа равны, если каждое из них делится на другое.
19. Через всякую точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной.
20. Для любых двух различных действительных чисел найдется число, расположенное между ними.
21. Если всякий разумный философ – циник и только женщины являются разумными философами, то тогда, если существуют разумные философы, то некоторые из женщин циничны.
22. Не всякий, в ком есть упорство, может изучить логику, но всякий, изучивший логику, обладает упорством.
23. Если всякий предок предка данного человека есть также предок того же человека и никакой человек не есть предок самого себя, то существует некто, не имеющий предков.
24. Если всякий друг моего друга – мой друг, то не всякий враг моего друга – мой враг.
25. Всякий, кто находится в здравом уме, может понимать математику; ни один из сыновей Гегеля не может понимать математику; сумасшедшие не допускаются к голосованию, следовательно, никто из сыновей Гегеля не допускается к голосованию.
26. Неверно, что не все фирмы уделяют внимание накоплению опыта всеми своими сотрудниками, значит, все сотрудники всех фирм опытны.
27. Теперь всякий скажет, что ничего не знает, но существует информация, которую любой с удовольствием передаст всем окружающим.
28. Когда я пьян, а пьян всегда я, ничто меня не устрашит и никакая сила ада мое блаженство не смутит.
29. С юридической точки зрения все однотипные преступления похожи, следовательно, имеются стадии, которые возможны во всех преступлениях с материальным составом.
30. Всегда имеются причины, не способствующие положительной мотивации всех работников, но есть универсальные факторы для этого, поэтому в отдельные моменты для некоторых работников надо, чтобы нашлись особые подходы к мотивации, и в любое время надо применять универсальные подходы.
ЛИТЕРАТУРА
1. Воротников в математическую логику: Учеб. пособие. – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 1996. – 128 с.
3. Гиндикин логики в задачах. – М.: Наука,1972. – 288 с.
4. Гладкий математической логики. – Калинин: Изд-во Калининского гос. ун-та, 1977. – 84 с.
6. Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику: Пер. с англ. – М.: ИЛ, 1963. – 487 с.
7. Клини логика: Пер. с англ. – М.: Мир, 1973. – 368 с.
11. Введение в математическую логику: Пер. с англ. – М.: Наука, 1984. – 320 с.
12. Язык логики. – М.: Наука, 1969. – 214 с.
13. Введение в математическую логику. Т.1: Пер. с англ. – М.: ИЛ, 1960. – 484 с.
14. Шенфилд Дж. Математическая логика: Пер. с англ. – М.: Наука, 1975. – 528 с.
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
Сергей Михайлович Воротников
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ ЛОГИКУ
Подписано в печать 24.06.02.
Формат 60 х 84 1/8. Бумага 80 г/м2. Отпечатано на ризографе.
Усл. печ. л. 7,49. Уч.-изд. л. 3,79. Тираж 200.
Государственного образовательного учреждения
«Комсомольский-на-Амуре государственный технический университет»




































 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ