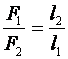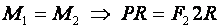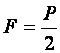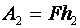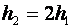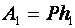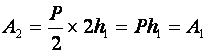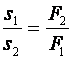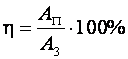Неподвижный блок применяют для подъема грузов потому что

Простые механизмы. Блок.

Одним из простых механизмов является блок. Блок — это колесо с желобом, по которому пропущена веревка или трос. Используется блок, как и все простые механизмы, для преобразования силы — т.е. изменения направления и модуля приложенной силы.

Блоки бывают подвижные и неподвижные. Рассмотрим каждый случай подробно.

Неподвижный блок.

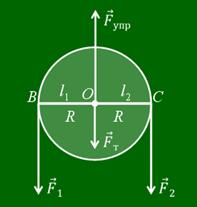
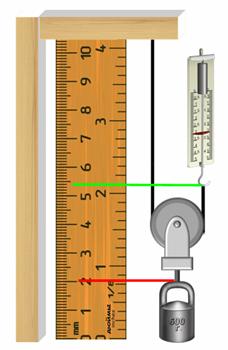
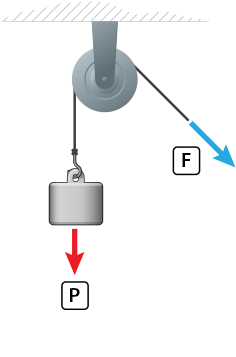
Неподвижный блок — это блок, ось которого (точка О на рисунке) закреплена, и блок при подъеме грузов не опускается и не поднимается.

Такой блок можно рассматривать как рычаг первого рода, у которого оба плеча равны между собой, и равны радиусу колеса блока:

Так как плечи рычага равны, то мы не получим выигрыша в силе. Проверим это, используя формулу равновесия рычага:

В нашем случае неподвижного блока:

Действительно, для того чтобы уравновесить силу на одном конце веревки, перекинутой через блок, нам необходимо приложить такую же силу на другом конце. Поэтому неподвижные блоки используют в том случае, если удобнее изменить направление силы, для совершения работы. Например, удобнее поднимать груз, удерживая веревку при помощи своего веса, поэтому на рисунке экспериментатор использует неподвижный блок.

Используя комбинации из неподвижных блоков можно менять направление силы как угодно:

И в этом случае, используя уже два неподвижных блока — мы не получаем выигрыша в силе, зато изменили направление приложения силы, теперь для поднятия груза силу мы должны приложить в горизонтальном направлении.

Подвижный блок

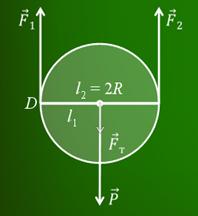
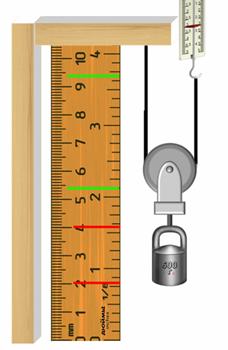
Подвижный блок — это блок, ось которого не закреплена, а поднимается вместе с грузом. Изобразим подвижный блок находящийся в равновесии, отметим на рисунке силы, действующие на систему, а также плечи приложения этих сил:

Подвижный блок можно сравнить с рычагом второго рода. Действительно: точка опоры О лежит по одну сторону от точки приложения сил, отрезок ОА — плечо силы P

Источник

Блоки. Золотое правило механики

Урок 39. Физика 7 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Блоки. Золотое правило механики»

Блоки. Золотое правило механики

«Мыслящий ум не чувствует себя счастливым,

пока ему не удастся связать воедино разрозненные

факты, им наблюдаемые»

Данная тема посвящена изучению блоков. А также рассмотрению «Золотого правила механики».

В прошлых темах говорилось о простых механизмах, таких как рычаг. Рычаг — это любое твердое тело, которое может поворачиваться относительно неподвижной опоры или оси.

Рычаги бывают двух видов – рычаг первого и рычаг второго рода. Рычаг первого рода — это рычаг, ось вращения которого расположена между точками приложения сил, а сами силы направлены в одну сторону. Рычаг второго рода — это рычаг, ось вращения которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу.

Вывели условие равновесия рычага, согласно которому, рычаг находится в равновесии при условии, что приложенные к нему силы обратно пропорциональны длинам их плеч.

Рассмотрели момент силы — физическую величину, равную произведению модуля силы, вращающей тело, на ее плечо. И сформулировали условие равновесия рычага через правило моментов, согласно которому, рычаг под действием двух создающих моменты сил находится в равновесии в том случае, если момент силы, вращающей рычаг по часовой стрелке, равен моменту силы, вращающей рычаг против часовой стрелки.

Однако, помимо рычагов, нередко для подъема грузов используется и простой блок или система блоков. Особенно часто применяются блоки на стройплощадках, в портах и на складах. Любой блок представляет собой колесо с жёлобом, укрепленное в обойме. По жёлобу блока пропускают веревку, трос или цепь.

А какие бывают блоки? И как они преобразуют силу?

Если ось блока закреплена и при подъеме грузов она не опускается и не поднимается, то блок называется неподвижным. Такой блок можно рассматривать как равноплечный рычаг, у которого плечи сил равны радиусу колеса. Дает ли такой блок выигрыш в силе? Поставим опыт. Возьмем груз весом 3 Н и подвесим к одному концу перекинутой через блок нити, а к другому прикрепим динамометр. При равномерном подъеме груза динамометр покажет силу, равную весу груза, т.е. 3 Н. Изобразим схематически силы, действующие на блок.

Это сила упругости нити, равная весу груза, сила упругости нити, равная приложенной к динамометру силе, сила тяжести, действующая на блок и сила упругости оси блока. Как видно из рисунка, плечи сил тяжести и упругости блока равны нулю. Значит и их моменты относительно оси равны нулю. Плечи сил упругости нити один и два равны между собой как радиусы блока. В состоянии равновесия блока моменты сил F₁ и F₂ должны быть равны. А раз равны моменты этих сил, то и сами силы равны между собой. Иными словами, прилагаемая сила равна весу груза. Таким образом, неподвижный блок не дает выигрыша в силе, а лишь изменяет ее направление.

Зачем применять неподвижный блок, если выигрыша в силе нет? Ведь с таким же успехом для подъема груза можно было бы использовать любую перекладин. Можно, но проигрышно, так как придется преодолевать силу трения скольжения веревки по перекладине, которая значительно больше силы трения качения в подшипнике блока.

А может ли все-таки блок дать выигрыш в силе? Рассмотрим другой вид блока — подвижный блок. Подвижным называется блок, ось вращения которого при подъеме груза движется вместе с грузом.

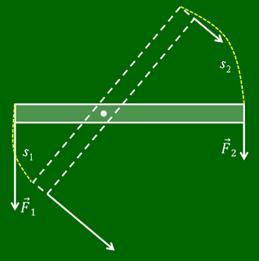
Подвесим к такому блоку груз весом 6 Н. Один конец перекинутой через блок нити закрепим, а за другой будем равномерно поднимать груз при помощи динамометра. Динамометр показывает, что прилагаемая к концу веревки сила равна 3 Н, т. е. в два раза меньше веса груза. Следовательно, подвижный блок дает выигрыш в силе примерно в 2 раза. Почему?

На блок действуют вес груза, силы упругости нити, которые равны между собой, и сила тяжести блока. При этом, чаще всего, силой тяжести блока пренебрегают, так как она, как правило, намного меньше веса груза. При движении груза подвижный блок поворачивается относительно точки D. Следовательно, подвижный блок — это рычаг второго рода. Запишем условие равновесия для него через правило моментов. Из рисунка видно, что плечо веса груза равно радиусу блока, а плечо второй силы — двум радиусам блока.

С учетом того, что сила F₂ равна силе F, прилагаемой к концу веревки, и используя основное свойство пропорции, получим

Таким образом, можно сделать вывод о том, что подвижный блок дает выигрыш в силе в два раза.

Теперь можно сделать главный вывод о том, что при использования простых механизмов, мы можем получить выигрыш в силе.

Встает логичный вопрос: А можно ли с помощью простого механизма получить выигрыш в работе? Если прилагаемая сила меньше веса груза, то будет ли совершенная ею работа меньше работы по подъему груза без использования механизма?

Поставим опыт. Будем поднимать равномерно груз на некоторую высоту с помощью подвижного блока (силой тяжести блока и силой трения пренебрегаем).

Работа силы, приложенной к нити, равна произведению приложенной к нити силы и высоты подъема ее точки приложения.

Как видно из рисунка, высота подъема точки приложения силы в два раза больше высоты подъема груза. Работа по подъему груза равна по модулю произведению веса груза и высоты подъема груза.

Теперь сравним две работы. При этом учтем, что сила, приложенная к концу веревки примерно в два раза меньше веса груза.

Принимая этот факт во внимание, получим, что работа по подъему груза равна работе приложенной к нити силы.

Таким образом, использование подвижного блока не дает выигрыша в работе. Так как, имеется выигрыш в 2 раза в силе и проигрыш в 2 раза в пути.

Аналогично можно подойти к рассмотрению рычага. Для этого на рычаге уравновешиваются 2 разные по модулю силы, и рычаг приводится в движение.

Если измерить расстояния, пройденные большей и меньшей силами, и модули этих сил, то получим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам.

Таким образом, как и в случае с подвижным блоком, можем заключить, что действуя на длинное плечо рычага, выигрываем в силе, но при этом во столько же раз проигрываем в пути. Так как произведение силы на путь есть работа, то и в этом случае, выигрыш в работе не получается.

Как показала многовековая практика, ни один механизм не дает выигрыша в работе. Это утверждение получило название «Золотое правило механики». Если с помощью какого-либо простого механизма выигрываем в силе, то во столько же раз проигрываем в пути.

Можно ли при сравнении работ ставить между ними строгое равенство? Ведь делая тот или иной вывод, вводилось условие о том, что силой тяжести, действующей на блок, и силой трения в блоке можно пренебречь? Однако трение существует. Оно присутствует во всех механизмах. И сила тяжести, которая действует на сам блок, пусть даже и небольшая, тоже есть. Даже если не происходит подъема простого механизма или его частей (как в случае неподвижного блока), необходимо прилагать дополнительную силу на приведение его в движение, т. е. на преодоление инертности механизма. Поэтому прилагаемая к механизму сила должна реально совершать большую работу, чем полезная работа по подъему груза.

Работа силы, приложенной к механизму, называется затраченной или полной работой. А полезной является работа по поднятию только самого груза.

Если рассмотреть любой механизм, то полезная работа всегда составляет лишь некоторую часть полной работы. Обозначим полезную работу как A_П, а затраченную — A₃. Отношение полезной работы, к работе затраченной, называется коэффициентом полезного действия механизма (сокращенно КПД).

Коэффициент полезного действия обозначается маленькой греческой буквой h (эта) и, чаще всего, выражается в процентах. Так как полезная работа всегда меньше совершенной, то коэффициент полезного действия механизма всегда меньше 100%.

Задача 1. Какую минимальную силу нужно приложить к концу веревки для подъема мешка цемента массой 50 кг с помощью подвижного блока? На какую высоту будет поднят мешок при совершении этой силой работы в 2500 Дж?

Задача 2. Плита массой 120 кг была равномерно поднята с помощью подвижного блока на высоту 16 м за промежуток времени, равный 40 с. Считая коэффициент полезного действия равным 80%, а массу блока — 10 кг, определите полную работу и развиваемую мощность.

– Блок — это одна из разновидностей рычага, который представляет собой колесо с желобом, укрепленное в обойме. Различают подвижный и неподвижный блоки.

– Неподвижный блок — это блок, ось вращения которого закреплена и при подъеме грузов она не поднимается и не опускается.

– Подвижный блок — это блок, ось вращения которого поднимается и опускается вместе с грузом.

– Неподвижный блок не дает выигрыша в силе, а лишь меняет ее направление.

– Подвижный блок, если пренебречь трением и весом самого блока, дает выигрыш в силе в два раза.

– «Золотое правило механики», согласно которому во сколько раз выигрываем в силе, во столько же раз проигрываем в пути.

– Коэффициента полезного действия механизма показывает, какую часть от совершенной прилагаемой силой работы составляет полезная работа.

– Полезная работа всегда меньше совершенной. Коэффициент полезного действия любого механизма меньше 100%.

Источник

Неподвижный блок

Что такое неподвижный блок в физике

Неподвижный блок — это диск, который вращается вокруг своей оси, и имеет желоб по окружности. Желоб предназначен для скольжения в нем нити (цепи, ремня, каната и т.д.). У неподвижного блока ось закреплена, и при подъеме грузов не поднимается и не опускается.

Неподвижный блок можно представить в виде равноплечего рычага, у которого плечи сил равны радиусу колеса.

В задачах часто используют модель идеального блока.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В идеальном блоке используется идеальная нерастяжимая и невесомая нить. Проскальзывание нити и силы трения отсутствуют. Сам блок также является невесомым.

Свойства идеального блока:

Для чего используется, примеры применения

Неподвижные блоки используют для изменения направления прикладываемой силы.

Неподвижные блоки используются:

Какой выигрыш в силе дает неподвижный блок

Неподвижный блок не дает выигрыша в силе. Для того чтобы поднять груз прикрепленный к одному концу веревки, нужно приложить такую же силу к другому концу веревки.

Неподвижный блок используют не для выигрыша в силе, а для изменения направления прикладываемой силы. Например, тянуть веревку вниз может быть значительно удобнее, чем поднимать наверх.

У неподвижного блока нет выигрыша в силе, но нет и проигрыша в расстоянии. На какое расстояние опустится веревка, к которой применяют силу, на такое же расстояние поднимется груз.

КПД реального неподвижного блока всегда будет меньше единицы. Ведь часть работы неподвижного блока тратится на силу трения веревки о желоб.

Виды неподвижных блоков и их свойства

Неподвижные блоки различаются по материалу изготовления, а также по наличию дополнительных элементов.

Материал изготовления диска и тросов влияет на силу трения внутри блока и грузоподъемность блока.

По наличию дополнительных элементов блоки бывают:

Различные дополнительные элементы позволяют крепить разные грузы.

Неподвижные блоки в системах блоков

Для улучшения свойств неподвижные блоки часто используют в системах блоков.

Система из двух неподвижных блоков различного диаметра, насаженных на общую ось, обеспечивает выигрыш в силе или скорости. Ведь плечи сил в такой системе будут неравными.

Полиспаст — система из неподвижных и подвижных блоков.

Полиспаст позволяет получить выигрыш в силе в несколько раз. А также дает возможность менять направление прикладываемой силы.

Как найти момент силы и работу, формулы

Сила, которую нужно приложить для поднятия груза, равна силе, с которой действует на подвес груз.

Согласно правилу моментов:

Где F₁ — сила, с которой действует на точку подвеса груз, F₂ — сила, которую прикладывают для того, чтобы груз поднять, I₁ — радиус блока.

Формула приобретает вид:

Условия равновесия неподвижного блока:

Где F — сила, которую нужно приложить, m — масса груза, g — ускорение свободного падения, f — коэффициент сопротивления в блоке.

Для идеального блока коэффициент сопротивления не учитывается.

Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, значит, равны работы.

Источник

Простые механизмы.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.

Рычаг.

Рис. 1. Рычаг

Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.

Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).

Неподвижный блок.

Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.

На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).

Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.

Подвижный блок.

Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).

Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.

Наклонная плоскость.

Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.

Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:

Проектируем на ось :

Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.

Широко применяемыми разновидностями наклонной плоскости являются клин и винт.

Золотое правило механики.

Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.

т. е. той же величине, что и без использования рычага.

т. е. ту же самую, что и при вертикальном поднятии груза.

Данные факты служат проявлениями так называемого золотого правила механики.

Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.

Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.

КПД механизма.

На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.

Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.

Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.

Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:

КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.

Ускорения нет, поэтому силы, действующие на груз, уравновешены:

Проектируем на ось X:

Проектируем на ось Y:

Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:

Источник

Применение закона равновесия рычага к блоку

Содержание

Мы называем рычагом любое твердое тело, которое может вращаться вокруг неподвижной опоры. Одной из разновидностей рычага является такой простой механизм как блок.

Блок представляет собой собой колесо (диск) с желобом, укрепленное в обойме.

По желобу блока пропускают трос, цепь или веревку. Если блок – это разновидность рычага, то применим ли к нему закон равновесия ($\frac = \frac$)?

Для того чтобы ответить на этот вопрос, в данном уроке мы более подробно изучим устройство блока. Блоки бывают двух видов: подвижный и неподвижный. Рассмотрим принцип работы каждого из них.

Неподвижный блок

Неподвижный блок – это блок, ось которого закреплена и при подъеме груза не поднимается и не опускается.

Неподвижный блок изображен на рисунке 1.

Рисунок 1. Неподвижный блок.

Если поднимать груз без использования блока, мы будем использовать только силу наших мышц. Если мы используем блок, то тогда мы можем тянуть за веревку вниз, использую и силу наших мышц, и вес своего тела. Таким образом поднять груз намного легче.

Подвижный блок

Подвижный блок – это блок, ось которого поднимается и опускается вместе с грузом.

Подвижный блок изображен на рисунке 2.

Рисунок 2. Подвижный блок.

Тогда наше выражение примет следующий вид:

$F = \frac

<2>$,

Подвижный блок дает выигрыш в силе в 2 раза.

Применение комбинаций блоков

На практике часто применяют комбинацию (систему) неподвижного и подвижного блоков (рисунок 3). Такая комбинация называется полиспастом блоков.

Рисунок 3. Комбинации подвижного и неподвижного блоков.

При таком варианте использования блоков мы также получаем выигрыш в силе в 2 раза. Обеспечивает его подвижный блок. С помощью неподвижного блока изменяем направление силы. Он позволяет занять нам более удобное положение – так мы можем поднимать груз, стоя на земле.

На практике полиспаст является частью механизма подъема у подъемных кранов (рисунок 4).

Рисунок 4. Крюковой подвес с полиспастом.

Альпинисты используют систему блоков для натяжения перил и переправ, а также для подъема пострадавших из ущелий, трещин и др. (рисунок 5).

Источник