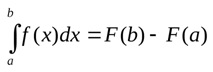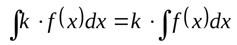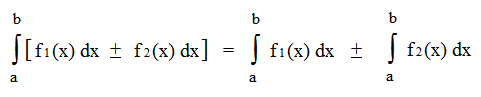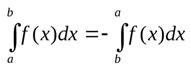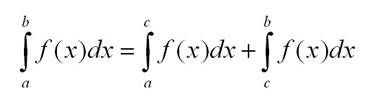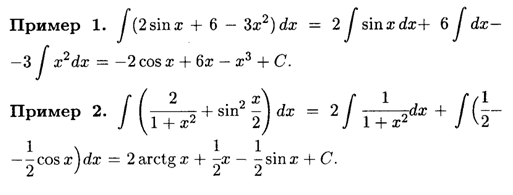Неопределенный интеграл что это

Первообразная функция и неопределенный интеграл

Первообразная

Определение первообразной функции

Можно прочесть двумя способами:

Правила вычисления первообразных

Запомни!

Любая функция F(x) = х 2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.

Связь между графиками функции и ее первообразной:

Неопределенный интеграл

Определение:

Свойства неопределённого интеграла

Таблица первообразных и неопределенных интегралов

Функция

Первообразная

F(x) + C

Неопределенные интегралы

\int f(x) dx = F(x) + C

Формула Ньютона–Лейбница

Пусть f (х) данная функция, F её произвольная первообразная.

То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.

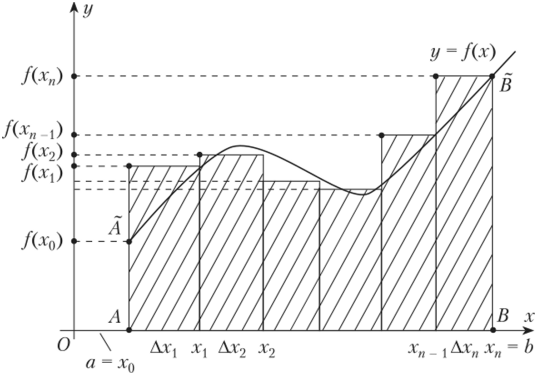
Площадь криволинейной трапеции

Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

Площадь криволинейной трапеции находят по формуле Ньютона-Лейбница:

Источник

Определение и свойства неопределенного интеграла. Основные методы интегрирования.

Ранее нами была рассмотрена задача о нахождении мгновенной скорости материальной точки по заданному закону ее движения. Если \(s=s(t)\) — путь, пройденный точкой за время \(t\) от начала движения, то мгновенная скорость \(v\) в момент \(t\) равна производной функции \(s(t)\), то есть
$$
v=s'(t).\nonumber
$$
В физике встречается обратная задача: по заданной скорости \(v=v(t)\) найти закон движения, то есть найти такую функцию \(s(t)\) производная которой равна \(v(t)\).

Первообразная.

Пусть функции \(f(x)\) и \(F(x)\) определены на интервале \((a,b)\). Если функция \(F(x)\) имеет производную на интервале \((a,b)\) и если для всех \(x\in (a,b)\) выполняется равенство
$$
F'(x)=f(x),\label
$$
то функция \(F(x)\) называется первообразной для функции \(f(x)\) на интервале \((a,b)\).

Понятие первообразной можно ввести и для других промежутков (полуинтервала — конечного или бесконечного, отрезка).

Дадим определение первообразной на отрезке. Если функции \(f(x)\) и \(F(x)\) определены на отрезке \([a,b]\), причем функция \(F\) дифференцируема на интервале \((a,b)\), непрерывна на отрезке \([a,b]\) и для всех \(x\in (a,b)\) выполняется равенство \eqref, то функцию \(F(x)\) назовем первообразной для функции \(f(x)\) на отрезке \([a,b]\).

Если \(F(x)\) — первообразная для функции \(f(x)\) на интервале \((a,b)\), то функция \(F(x)+C\) при любом значении \(C=\operatorname\) также является первообразной для \(f(x)\).

Справедливо и обратное утверждение.

Если \(F_1(x)\) и \(F_2(x)\) — две первообразные для функции \(f(x)\) на интервале \((a,b)\), то для всех \(x\in (a,b)\) выполняется равенство
$$
F_2(x)=F_1(x)+C,\label
$$
где \(C\) — постоянная.

\(\circ\) Обозначим \(\Phi(x)=F_2(x)-F_1(x)\). По определению первообразной в силу условий теоремы для всех \(x\in (a,b)\) выполняются равенства
$$
F_1′(x)=f(x),\quad F_2′(x)=f(x),\nonumber
$$
откуда следует, что функция \(\Phi(x)\) дифференцируема на интервале \((a,b)\) и для всех \(x\in(a,b)\) имеет место равенство
$$
\Phi'(x)=0.\nonumber
$$
Согласно первому следствию из теоремы Лагранжа \(\Phi(x)=C=\operatorname\) для всех \(x\in (a,b)\) или \(F_2(x)-F_1(x)=C\), то есть справедливо равенство \eqref. \(\bullet\)

Таким образом, для данной функции \(f(x)\) ее первообразная \(F(x)\) определяется неоднозначно, с точностью до постоянной. Для того чтобы из совокупности первообразных выделить какую-либо первообразную \(F_1(x)\), достаточно указать точку \(M_0(x_0,y_0)\), принадлежащую графику функции \(y=F(x)\).

Для функции \(f(x)=\displaystyle \frac<1>\) найти такую первообразную \(F_1(x)\), график которой проходит через точку \((1,2)\).

\(\triangle\) Совокупность всех первообразных функции \(\displaystyle \frac<1>\) описывается формулой
$$
F(x)=-\frac<1>+C.\nonumber
$$

По условию \(F_1(1)=2\), то есть \(2=-1+C\), откуда \(C=3\). Следовательно, \(F_1(x)=3-\displaystyle \frac<1>\). \(\blacktriangle\)

В дальнейшем (гл. VII, § 36) будет доказано, что первообразная существует для любой функции, непрерывной на отрезке (или интервале).

Понятие неопределенного интеграла.

Совокупность всех первообразных для функции \(f(x)\) на некотором промежутке \(\Delta\) называют неопределенным интегралом от функции \(f\) на этом промежутке, обозначают символом \(\displaystyle \int f(x)dx\) и пишут
$$
\int f(x)dx=F(x)+C.\label
$$

Здесь \(F(x)\) — какая-нибудь первообразная функции \(f\) на промежутке \(\Delta\), \(C\) — произвольная постоянная. Знак \(\displaystyle \int\) называется знаком интеграла, \(f\) — подынтегральной функцией, \(f(x)dx\) — подынтегральным выражением.

Подынтегральное выражение можно записать в виде \(F'(x)\) или в виде \(dF(x)\), то есть
$$
f(x)dx=dF(x).\label
$$

Операцию нахождения неопределенного интеграла от данной функции, которая является обратной операции дифференцирования, называют интегрированием. Поэтому любую формулу для производной, то есть формулу вида \(F'(x)=f(x)\), можно записать в виде \eqref.

Используя таблицу производных, можно найти интегралы от некоторых элементарных функций. Например, из равенства \((\sin x)’=\cos x\) следует, что \(\displaystyle \int\cos x dx=\sin x+C\).

Свойства неопределенного интеграла.

\(\circ\) Из равенства \eqref следует, что
$$
d\left(\int f(x)dx\right)=d(F(x) + C) = dF(x),\nonumber
$$
так как \(dC = 0\). \(\bullet\)

Согласно формуле \eqref знаки дифференциала и интеграла взаимно уничтожаются, если знак дифференциала стоит перед знаком интеграла.

\(\circ\) Равенство \eqref следует из равенств \eqref и \eqref. \(\bullet\)

Соотношение \eqref показывает, что и в случае, когда знак интеграла стоит перед знаком дифференциала, эти знаки также взаимно уничтожается (если отбросить постоянную \(C\)).

Если функции \(f(x)\) и \(g(x)\) имеют на некотором промежутке первообразные, то для любых \(\alpha\in R, \ \beta\in R\) таких, что \(\alpha^2+\beta^2\neq 0\), функция \(\varphi(x) = \alpha f(x)+\beta g(x)\) также имеет первообразную на этом промежутке, причем
$$
\int\left(\alpha f(x)+\beta g(x)\right)dx=\alpha\int f(x)dx+\beta\int g(x).\label
$$

\(\circ\) Пусть \(F\) и \(G\) — первообразные для функций \(f\) и \(g\) соответственно, тогда \(\Phi=\alpha F + \beta G\) — первообразная для функции \(\varphi\), так как \((\alpha F(x)+\beta G(x))’=\alpha f(x)+\beta g(x)\). Согласно определению интеграла левая часть \eqref состоит из функций вида \(\Phi(x)+C\), а правая часть — из функций вида \(\alpha F(x)+\alpha C_1+\beta G(x)+\beta C_2=\Phi(x)+\alpha C_1+\beta C_2\). Так как \(\alpha^2+\beta^2\neq 0\), то каждая функция вида \(\Phi(x)+C\) принадлежит совокупности функций \(\Phi(x)+\alpha C_1+\beta C_2\), и наоборот, то есть по заданному числу \(C\) можно найти \(C_1\) и \(C_2\), а по заданным \(C_1\) и \(C_2\) — число \(C\) такое, чтобы выполнялось равенство \(C=\alpha C_1+\beta C_2\). \(\bullet\)

Таким образом, интегрирование обладает свойством линейности: интеграл от линейной комбинации функций равен соответствующей линейной комбинации интегралов от рассматриваемых функций.

Найти \(\displaystyle \int f(x)dx\), если:

Дальнейшее расширение множества функций, интегралы от которых выражаются через элементарные функции, можно получить, если воспользоваться правилом дифференцирования сложной функции и правилом дифференцирования произведения двух функций.

Метод замены переменного (метод подстановки).

Пусть функция \(t=\varphi(x)\) определена и дифференцируема на промежутке \(\Delta\) и пусть \(\Delta_i=\varphi(\Delta)\) — множество значений функции \(\varphi\) на \(\Delta\).

Если функция \(U(t)\) определена и дифференцируема на \(\Delta_i\), причем
$$
U'(t)=u(t),\label
$$
то на промежутке \(\Delta\) определена и дифференцируема сложная функция \(F(x)=U(\varphi(x))\) и
$$
F'(x)=\left[U(\varphi(x))\right]’=U'(\varphi(x))\varphi'(x)=u(\varphi(x))\varphi'(x).\label
$$

Из равенств \eqref и \eqref следует, что если \(U(t)\) — первообразная для функции \(u(t)\), то \(U(\varphi(x))\) — первообразная для функции \(u(\varphi(x))\varphi'(x)\). Это означает, что если
$$
\int u(t) dt = U(t) + C,\label
$$
то
$$
\int u(\varphi(x))\varphi'(x)dx=U(\varphi(x)) + C,\label
$$
или
$$
\int u(\varphi(x))d\varphi(x)= U(\varphi(x)) + C.\label
$$

Формулу \eqref (или формулу \eqref) называют формулой интегрирования заменой переменного. Она получается из формулы \eqref, если вместо \(t\) подставить дифференцируемую функцию \(\varphi(x)\).

Формула \eqref дает возможность найти интеграл \(\displaystyle f(x)dx\), если функция \(f(x)\) представляется в виде \(f(x) = u(\varphi(x))\varphi'(x)\) и если известна первообразная функции \(u(t)\), то есть известен интеграл \eqref.

Отметим важные частные случаи формулы \eqref.

Приведем примеры применения формул \eqref-\eqref.

Источник

Теорема. Две различные первообразные одной и той же функции, определенной на

При этом f (x) называется подынтегральной функцией, f (x)dx – подынтегральным выражением, x – переменной интегрирования.

Согласно определению неопределенного интеграла можно написать:

Основные свойства неопределенного интеграла

1. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции (1,2).

Замечание. В формулах (1) и (2) знаки и уничтожают друга. В этом смысле интегрирование и дифференцирование являются взаимно обратными математическими операциями.

Свойства линейности неопределенного интеграла.

Таблица интегралов

Непосредственное интегрирование

Непосредственное интегрирование заключается в том, чтобы преобразовать подынтегральное выражение, если это возможно, так чтобы получился дифференциал f (x)dx, а затем в таблице
интегралов найти первообразную.

Пример 1.

который можно отыскать в таблице интегралов, где u(x) = sin x.

Пример 2.

Здесь мы умножили подынтегральную функцию и разделили на 2, затем внесли 2 под знак дифференциала. Заменим 2dx =d (2x +1) и получим табличный интеграл

Проверим результат дифференцированием:

Пример 3.

В данном примере мы применили прием подведения под знак дифференциала cosx и постоянной 1. cos xdx = d(1+ sin x).

Пример 4.

Метод подстановки

Пример 6.

Метод интегрирования по частям.

Иногда формула интегрирования по частям применяется несколько раз. Рассмотрим пример такого интеграла.

Замечание. Иногда применение формулы интегрирования по частям приводит к исходному интегралу, который в таком случае называется циклическим или круговым.

Источник

Первообразная и неопределенный интеграл, их свойства

Определение первообразной

Определение неопределенного интеграла

Имея заданный дифференциал функции, мы можем найти неизвестную функцию.

∫ f ( x ) d x ‘ = F ( x ) + C ‘ = f ( x )

∫ d ( F ( x ) ) = ∫ F ‘ ( x ) d x = ∫ f ( x ) d x = F ( x ) + C

∫ f ( x ) ± g ( x ) ) d x = ∫ f ( x ) d x ± ∫ g ( x ) d x

Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.

Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:

k · ∫ f ( x ) d x ‘ = k · ∫ d ( x ) d x ‘ = k · f ( x ) ∫ f ( x ) d x ± ∫ g ( x ) d x ‘ = ∫ f ( x ) d x ‘ ± ∫ g ( x ) d x ‘ = f ( x ) ± g ( x )

Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.

Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.

Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.

Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.

Решение

Используя таблицу производных основных элементарных функций получаем

d ( ln x ) = ( ln x ) ‘ d x = d x x = f ( x ) d x ∫ f ( x ) d x = ∫ d x x = ∫ d ( ln ( x ) )

Ответ: f ( x ) = 1 x = ln ( x ) + 1

Необходимо найти неопределенный интеграл ∫ 2 sin x 2 cos x 2 d x и проверить результат вычисления дифференцированием.

Решение

Используем таблицу производных для тригонометрических функций, получим:

Проверим полученный результат дифференцированием.

В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.

Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.

Подробнее эту тему мы рассмотрим в следующем разделе «Таблица первообразных (таблица неопределенных интегралов)».

Источник

Интегралы – что это, как решать, примеры решений и объяснение для чайников

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Интеграл – что это?

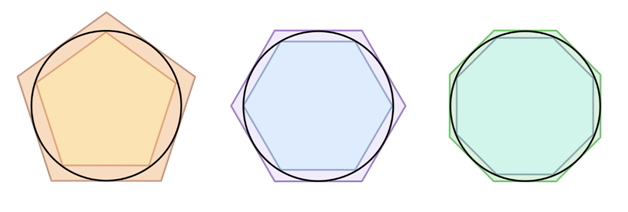
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:

Источник