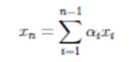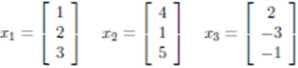Нелинейная алгебра что это

Нелинейная алгебра: почему 3 детей – это больше, чем 2+1

Ксения Андреева, мама троих погодок, бизнес-леди, писательница, «Вице-Миссис Санкт-Петербург» и финалистка конкурса красоты и талантов «Миссис Россия – 2018» рассказывает о свою историю о том, что происходит в семье после рождения третьего ребенка. Опыт Ксении особенно интересен, с учетом того, что ее погодкам – всего 4.5, 2.11 и 1.2 года, и она старается сохранить в жизни баланс между материнством, работой, творчеством и спортом, о чем и рассказывает в своей новой книге «Мама-менеджмент».

Быть мамой – это не только сказочное счастье, но и адский труд. Вы знаете и без меня: каждая из нас, вне зависимости от количества детей, крутится и вертится, стараясь решить все возникающие крошечные и не очень вопросы, образующие вместе огромный ком. И этот ком катится на нас каждый день, начиная с самого утра и до позднего вечера, и каждый день мы пытаемся его чуть-чуть растрясти, увернуться от него, направить в безопасное русло.

Когда рождается первый ребенок, жизнь, вне всякого сомнения, делится на «до» и «после». Однако, на мой взгляд, существенным тут оказывается не просто объем дел или физическая нагрузка, а изменение нашего состояния – из девочки, девушки, женщины мы становимся – матерью, целой вселенной для одного маленького малыша. И, конечно, это принципиально другое отношение к миру, иное чувство ответственности, а также отношение к себе и своей жизни. Хотя моя первая беременность была не очень простой, но в момент рождения первого ребенка на меня мгновенно нахлынуло такое огромное море любви, что сразу стало ясно: жизнь только начинается, вот оно – мое счастье, и теперь я могу ощутить его в полной мере. Однако – предстояло наладить жизнь в плане работы и заняться приведением себя в форму после набора 18 кг… В общем – вызовы стояли и я постепенно начала их решать.

После рождения второго погодки, на мой взгляд, изменение общей жизненной модели было достаточно незначительное. Безусловно, разница есть! Ведь появляется еще один член семьи, который нуждается в маминой заботе и внимании. И в материнском сердце становится в два раза больше любви. Но в плане каждодневных процессов ничего критически не меняется – кормление, прогулки, сон, переодевания, купания, игры и прочие занятия, в общем – суть вся та же. Можно сказать, что второй ребенок с небольшой разницей в возрасте идет как дополнительный модуль сложности к тому же жизненному режиму. Тем более что у мамы все еще приходится по одной руке на каждого ребенка.

Конечно, далее у меня самой возникает очень интересный вопрос, может ли стать столь же радикальным рождение четвертого, пятого ребенка и далее. Судя по тому, что говорят мои более многодетные, чем я, подруги – нет, тут процессы, по сравнению с тремя детьми, особо не меняются. Но, конечно, увеличивается «уровень сложности». Впрочем, я уверена, что многое зависит и от характера самих детей, и это тоже влияет на «нелинейную алгебру». В общем, кто знает. Надеюсь, что когда-нибудь и этот опыт у меня произойдет, а пока что не буду загадывать и сосредоточусь на том, как охватить то, что уже есть в жизни.

Источник

Линейная алгебра: пробный заезд

Аналит, линейка, линал — эти слова ассоциируются скорее с фразой «сдать и забыть», а не с тем, для чего на самом деле нужен замечательный раздел математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и разберемся, что же в нем хорошего и почему он так полезен в приложениях.

Часто первое знакомство с линейной алгеброй выглядит как-то так:

Не очень вдохновляет, правда? Сразу возникает два вопроса: откуда это все взялось и зачем оно нужно.

Начнем с практики

Когда я занимался вычислительной гидродинамикой (CFD), один из коллег говорил: «Мы не решаем уравнения Навье-Стокса. Мы обращаем матрицы.» И действительно, линейная алгебра — «рабочая лошадка» вычислительной математики:

Попробую проиллюстрировать эту связь на более простом примере, чем гидродинамика.

Пусть у нас есть тонкий металлический стержень с закрепленными концами, температура которых поддерживается равной нулю. Начнем греть стержень с помощью распределенного источника тепла, выделяющего q(x) Джоулей в секунду на единицу длины стержня в окрестности точки x. Какая температура t=t(x) установится? Сделаем очень грубый набросок модели. Когда установится равновесие, для каждого отрезка [x-h, x+h] нашего стержня приток тепла от источника должен быть равен сумме потоков тепла через границы отрезка. Если h достаточно мало, то с точностью до констант (в которые войдет h, да простят мне это читатели) это равенство можно записать так:

где Q_x-h — поток тепла через левую границу, а Q_x+h — через правую. Согласно закону Фурье тепловой поток пропорционален разности температур (ведь если нырнуть в бассейн, то в первые секунды будет холоднее всего). Поэтому (с точностью до констант, содержащих h)

где мы уже учли граничные условия, а q_i=q(x_i). Ну вот мы и получили систему линейных уравнений:

В качестве еще одного примера приведу известную задачу о ссылочном ранжировании страниц одного сайта (или интернета в целом).
Есть N страниц, каждая из которых может содержать ссылки на другие страницы. Требуется определить, какие страницы являются наиболее важными. Как именно измерять «важность» — часть задачи. Мы будем представлять ее количественно в виде неотрицательного числа (веса). Начнем с естественного предположения: чем больше ссылок на данную страницу, тем больше ее вес. В этом подходе есть следующий недостаток: мы не учитываем вес ссылающихся страниц. Логично, что ссылка со страницы, имеющий больший вес, должна иметь большее значение. Эти рассуждения приводят нас к такой модели:

где a_ij — количество ссылок на i-ую страницу с j-ой, разделенное на общее количество ссылок с j-й страницы. Эту формулу можно читать так: вес i-й страницы равен сумме произведений веса j-й страницы на долю ссылок с j-й страницы на i-ую. Таким образом, мы свели нашу задачу к системе линейных уравнений. Более того, вектор весов p оказывается собственным вектором матрицы A, отвечающим собственному значению 1:

Существование этого вектора (строго говоря, для немного модифицированной матрицы A) гарантируется теоремой Фробениуса-Перрона. А найти его можно методом простых итераций.

Итак, линейная алгебра — это очень универсальный набор идей и инструментов, которые можно применять в самых разных областях. Но бесплатен только сыр в мышеловке, и за универсальность приходится платить: некоторые определения и теоремы могут показаться излишне абстрактными и запутанными. Но это не так: на самом деле, многие абстракции призваны упрощать жизнь, а не усложнять ее. «Если это выглядит как утка, плавает как утка и крякает как утка, то, вероятно, это утка» — по сути абстракция, причем весьма удобная, если к ней привыкнуть. То же самое с линейной алгеброй. Чтобы проиллюстрировать этот момент немного конкретнее, давайте дополним наш «внешний осмотр» кратким обсуждением того, что внутри.

Теперь немного теории

Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство в другое. В основном рассматриваются линейные функции (удовлетворяющие соотношению f(α · x + β · y) = α · f(x) + β · f(y) для любых чисел α и β и любых векторов x и y). Бывают и нелинейные (например, квадратичные формы). Но прежде всего нужно понимать что такое вектор (и векторное пространство). И это не так тривиально, как могло бы показаться.

В учебниках и курсах обычно приводится абстрактное определение из 8 пунктов. Еще иногда говорят, что векторное пространство — это аддитивно записанная абелева группа в которой определено умножение на скаляры, удовлетворяющее 4 аксиомам. Но тем, кто впервые изучает линейную алгебру, это вряд ли поможет разобраться. Гораздо проще рассмотреть несколько конкретных примеров, и увидеть в них аналогию. А определение из 8 пунктов — всего лишь формализация этой аналогии. Поэтому перейдем сразу к примерам.

Знакомые всем со школы направленные отрезки конечно же являются векторами. Множество направленных отрезков — пример векторного пространства. Теперь рассмотрим многочлены. Их можно складывать друг с другом и умножать на числа. Обратите внимание: с точки зрения алгебры эти операции сложения многочленов и умножения многочлена на число работают точно по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) выполняется как для направленных отрезков, так и для многочленов. Поэтому множество многочленов является векторным пространством, а многочлены — векторами.

Если векторы не являются линейно зависимыми, то они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и компланарных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.)

Теперь у нас есть строгое определение координат. Но смысл не только в этом: по пути мы столкнулись с более фундаментальными (и менее заметными) понятиями линейной комбинации и линейной зависимости. А еще мы узнали что в n-мерном линейном пространстве не может быть больше, чем n линейно независимых векторов. Этот факт — один из краеугольных камней линейной алгебры.

Казалось бы, мы все еще знаем слишком мало, чтобы извлечь из этого хоть какую-то пользу. Однако уже сейчас мы можем решать задачи, на первый взгляд не имеющие отношения к линейной алгебре. Например, такую: даны многочлены p и q; существует ли многочлен от двух переменных R=R(x,y) такой, что R(p(t), q(t))=0 при всех t?

Тем временем наш «пробный заезд» подходит к концу. Но остается еще коротко обсудить различные способы изучения линейной алгебры. Ограничусь здесь небольшим обзором своего собственного опыта и попробую дать на основе него пару советов.

Википедия Книга — лучший источник знаний

Мое знакомство с линейной алгеброй началось с самостоятельного изучения книги О.В. Мантурова и Н.М. Матвеева «Курс высшей математики», когда я учился в школе. Эта книга — далеко не лучший (но и не худший) источник знаний в данной области. Просто она стала первым учебником по высшей математике, попавшим в мои руки, и ее содержание показалась мне более интересным, чем школьная программа. Хотя сейчас можно с уверенностью сказать: есть куча других книг, которые школьникам стоит (и будет не менее интересно) изучить в первую очередь. Например, «Как решают нестандартные задачи» (Канель-Белов А.Я., Ковальджи А.К.) или «Ленинградские математические кружки» (Генкин С.А., Итенберг И.В., Фомин Д.В.). Если же Вы возьметесь изучать линейную алгебру по книгам, то стоит запастись терпением: для достижения желаемого результата может потребоваться больше времени, чем кажется.

Своими основными знаниями линейной алгебры (и многих других разделов математики) я все же обязан Л.И. Коваленко — легендарному преподавателю МФТИ, семинары и консультации которой всегда собирали аншлаг. Сложно переоценить то внимание, которое она оказывала каждому студенту, до позднего вечера принимая задания и так называемые «карточки» — индивидуальные задачи. А еще во время этих сдач мы активно общались друг с другом. Все это позволяло не только быстрее освоить то, что написано в учебниках, но и то, чего там нет — интуицию, хитрые приемы и прочее.

Живое общение студентов с преподавателями (и друг с другом) ничто не заменит, и в этом преимущество традиционных курсов. Но когда я сам работал ассистентом и вел семинары, часто возникало желание некоторые вещи автоматизировать, чтобы на содержательное общение оставалось больше времени. Нужно ли студенту ждать встречи с преподавателем, чтобы получить стандартный ответ на стандартный вопрос? Или узнать правильно ли решена такая-то стандартная задача? Впрочем, не нужно недооценивать студентов: по большей части, они сами хорошо чувствуют когда делают «почти бессмысленную работу», и их это тоже демотивирует. Проверка доказательства или метода решения — это одно, но вот, скажем, проверку решения системы линейных уравнений можно практически полностью доверить компьютеру. Более того, во многих случаях можно автоматизировать не только проверку ответа, но и часть самого решения — например, элементарные преобразования матриц.

Источник

Нелинейная алгебра пространства- времени

В настоящей книге изложены основы малоизученной теории мультивекторных пространств (ТМП). Мультивекторные пространства (МП) являются новым классом векторрных пространств. Алгебра векторов в МП отличается от стандартной линейной векторной алгебры. Рассматриваются метрические свойства МП, вопросы образования базиса МП, изучаются преобразования сохраняющие метрику, а также геометрические и алгебраические свойства МП. Наряду с математическими приложениями, ТМП можно использовать для моделирования свойств физического пространства (ФП). ТМП позволяет по-новому определить размерность ФП и связать это фундаментальное свойство с размерностью алгебры векторов, ТМП описывает такие известные эффекты, как замедление времени, сокращение длины, Эффект Доплера, а также позволяет объснить геометрическими эффектами такие экспериментальные факты, как существование стабильных частиц и античастиц, наличие у частиц материи волн де Бройля. ТМП объясняет экспериментально регистируемую трехмерность пространства и прогнозирует существование «измерений», ортогональных к наблюдаемому трехмерному пространству. Математическая модель ФП на основе ТМП позволяет объединить в единое целое три наблюдаемых объекта: время, пространство, вещество.

Книга адресована широкому кругу читателей, интересующихся алгеброй и ее приложениями, предназначенными для описания свойств ФП.

Источник

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

kdnuggets

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:

Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

TimoElliott

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

Ортогональные матрицы

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

TimoElliott

Область значений и нуль-пространство матрицы

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают

Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx

), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

Собственные значения и собственные векторы

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

Источник