Некто заплатил за книжку на 120 рублей больше чем за тетрадь
Математика. 5 класс
Конспект урока
Перечень вопросов, рассматриваемых в теме:
— использование свойств арифметических действий при решении задач на части.
Сложить числа a и b – значит, к числу а прибавить b раз единицу.
Разность чисел a и b – это такое число, которое при сложении с числом b даёт число а.
Умножить число а на натуральное число b – значит, найти сумму а одинаковых слагаемых, каждое из которых равно b.
Теоретический материал для самостоятельного изучения
Задачи на части – само это название указывает на то, что рассматриваемые в них величины состоят из частей. В некоторых из них части представлены явно, в других – нужно суметь их выделить, приняв подходящую величину за одну часть и определив, из скольких таких частей состоят другие величины.
Рассмотрим задачу, в которой явно упоминаются равные части некоторой величины. Такие задачи обычно решаются с помощью простых рассуждений.
Задача 1. Для варенья из клубники на две части ягод берут три части сахара. Сколько сахара следует взять на 8 кг клубники?
Решение: по условию задачи дано 8 кг ягод, и это количество составляет две части. Найдём, сколько килограммов приходится на одну часть.
Сахара надо взять три такие же части, значит:
Теперь рассмотрим задачи, для решения которых некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.
Задача 2. Вика заплатила за учебник на 220 рублей больше, чем за прописи. Известно, что учебник дороже прописей в пять раз. Сколько стоит учебник?
Решение: представим стоимость в виде частей. Если стоимость прописей составляет одну часть, то стоимость учебника составляет пять таких же частей. Сделаем схематический рисунок.
На рисунке видно, что 220 рублей приходится на четыре части.
2) 220 : 4 = 55 (рублей) – приходится на одну часть, то есть на прописи.
3) 5 · 55 = 275 (рублей) – стоит книга.
Ответ: книга стоит 275 рублей.
Задача 3. На одном дереве сидит на 9 птиц больше, чем на втором, а на двух вместе 37 птиц. Сколько птиц сидит на каждом дереве?
Решение: сделаем схематический рисунок.
1) Если с первого дерева улетят 9 птиц, то на нём останется столько же птиц, сколько и на втором:
2) Найдём число птиц на каждом из деревьев:
3) Теперь вернём 9 птиц на первое дерево, получим:
Ответ: на первом дереве 23 птицы, на втором – 14.
Разбор решения заданий тренировочного модуля
№ 1. Всего в плацкартном вагоне на 84 места больше, чем в мягком. Известно, что в плацкартном вагоне в три раза больше спальных мест, чем в мягком вагоне. Сколько спальных мест в плацкартном вагоне?
№ 2. Для компота берут 2600 г фруктов. Абрикосы составляют 8 частей, а сливы – 5 частей. Сколько грамм абрикосов нужно для приготовления компота?
Задачи на части
Рассмотрим задачи, для решения которых некоторую величину можно принять за одну или несколько частей. При решении таких задач бывает полезно делать рисунки, облегчающие решение.
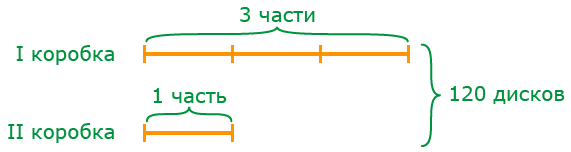
Задача 1. В двух коробках лежит 120 дисков в первой коробке в 3 раза больше дисков, чем во второй. Сколько дисков лежит в каждой коробке?
Решение: Представим содержимое коробок в виде частей. Если диски, находящиеся во второй коробке, составляют 1 часть, то в первой коробке 3 такие части. Сделаем схематический рисунок:
1) Сколько частей составляют 120 дисков?
2) Сколько дисков приходится на 1 часть?
3) Сколько дисков находится в первой коробке?
30 ·, 3 = 90 (дисков).
Ответ: 90 в первой коробке, 30 во второй.
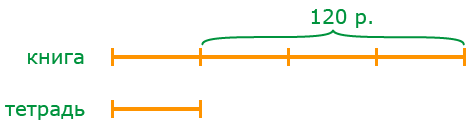
Задача 2. Некто заплатил за книгу на 120 рублей больше, чем за тетрадь. Известно, что книга дороже тетради в 4 раза. Сколько стоит книга?
Решение: Представим стоимость в виде частей. Если стоимость тетради составляет 1 часть, то стоимость книги составляет 4 такие же части. Сделаем схематический рисунок:
1) 4 — 1 = 3 (части) приходится на 120 рублей.
2) 120 : 3 = 40 (рублей) приходится на 1 часть.
3) 40 ·, 4 = 160 (рублей) стоит книга.
Ответ: Книга стоит 160 рублей.
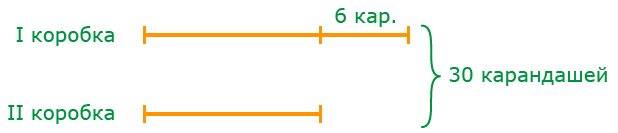
Задача 3. В первой коробке на 6 карандашей больше, чем во второй, а в двух вместе 30 карандашей. Сколько карандашей в каждой коробке?
Решение: Сделаем схематический рисунок:
1) Если из первой коробки вынуть 6 карандашей, в ней станет столько же карандашей, сколько и во второй:
2) Найдём число карандашей в каждой из коробок:
3) Теперь вернём 6 карандашей в первую коробку:
Ответ: В первой коробке 18 карандашей, во второй 12.
Задачи на части
Рассмотрим задачи, для решения которых некоторую величину можно принять за одну или несколько частей. При решении таких задач бывает полезно делать рисунки, облегчающие решение.
Задача 1. В двух коробках лежит 120 дисков — в первой коробке в 3 раза больше дисков, чем во второй. Сколько дисков лежит в каждой коробке?
Решение: Представим содержимое коробок в виде частей. Если диски, находящиеся во второй коробке, составляют 1 часть, то в первой коробке — 3 такие части. Сделаем схематический рисунок:
1) Сколько частей составляют 120 дисков?
2) Сколько дисков приходится на 1 часть?
3) Сколько дисков находится в первой коробке?
Ответ: 90 — в первой коробке, 30 — во второй.
Задача 2. Некто заплатил за книгу на 120 рублей больше, чем за тетрадь. Известно, что книга дороже тетради в 4 раза. Сколько стоит книга?
Решение: Представим стоимость в виде частей. Если стоимость тетради составляет 1 часть, то стоимость книги составляет 4 такие же части. Сделаем схематический рисунок:
2) 120 : 3 = 40 (рублей) — приходится на 1 часть.
3) 40 · 4 = 160 (рублей) — стоит книга.
Ответ: Книга стоит 160 рублей.
Задача 3. В первой коробке на 6 карандашей больше, чем во второй, а в двух вместе 30 карандашей. Сколько карандашей в каждой коробке?
Решение: Сделаем схематический рисунок:
1) Если из первой коробки вынуть 6 карандашей, в ней станет столько же карандашей, сколько и во второй:
2) Найдём число карандашей в каждой из коробок:
3) Теперь вернём 6 карандашей в первую коробку:
Ответ: В первой коробке 18 карандашей, во второй — 12.
Тренажер по задачам на части (5 класс)
Одним из сложных разделов математики является решение задач.
Сложным он является потому что для решения задач учащемуся необходимо иметь навык логического мышления, умения устанавливать связь в предметах и действиях, понимать смысл текста (условия задачи). Если учащийся не осмыслил условие задачи, то, естественно, и решить ее он не сможет.
Задачи на части. Само название вида задач говорит о том, что рассматриваемые в них величины состоят из частей . В некоторых из них части представлены явно, в других надо суметь выделить, приняв подходящую величину за 1 часть и определив, из скольких таких частей состоят другие величины, о которых идет речь в задаче.
Рассмотрим некоторые задачи данного вида, для решения которых некоторую величину можно принять за одну или несколько частей. При решении таких задач бывает полезно делать рисунки, облегчающие решение.
Задача 1. В двух коробках лежит 120 дисков – в первой коробке в 3 раза больше дисков, чем во второй. Сколько дисков лежит в каждой коробке?
Представим содержимое коробок в виде частей. Если диски, находящиеся во второй коробке, составляют 1 часть, то в первой коробке – 3 такие части. Сделаем схематический рисунок:
1) Сколько частей составляют 120 дисков?
2) Сколько дисков приходится на 1 часть?
3) Сколько дисков находится в первой коробке?
Ответ: 90 – в первой коробке, 30 – во второй.
Задача 2. Некто заплатил за книжку на 120 рублей больше, чем за тетрадь. Известно, что книга дороже тетради в 4 раза. Сколько стоит книга?
Представим стоимость в виде частей. Если стоимость тетради составляет 1 часть, то стоимость книги составляет 4 такие же части. Сделаем схематический рисунок:
2) 120 : 3 = 40 (рублей) – приходится на 1 часть.
3) 4 · 40 = 160 (рублей) – стоит книга.
Ответ: книга стоит 160 рублей.
Задача 3. В первой коробке на 6 карандашей больше, чем во второй, а в двух вместе 30 карандашей. Сколько карандашей в каждой коробке?
Сделаем схематический рисунок:
1) Если из первой коробки вынуть 6 карандашей, в ней станет столько же карандашей, сколько и во второй:
2) Найдём число карандашей в каждой из коробок:
3) Теперь вернём 6 карандашей в первую коробку:
Ответ: в первой коробке 18 карандашей, во второй – 12.
Решение: В задаче рассматриваются две пачки тетрадей. Всего тетрадей 70. В одной пачке на 10 тетрадей больше. Требуется узнать количество тетрадей в каждой пачке.
Изобразим при помощи отрезка количество тетрадей в первой и во второй пачке.



По чертежу видно, что если тетради во второй пачке составляют 1 часть всех тетрадей, то тетради в первой пачке составляют 1 часть и еще 10 тетрадей.
Если эти 10 тетрадей убрать из первой пачки, то в пачках станет поровну. Запишем решение по действиям.
1) 70 – 10 = 60 (т) – столько тетрадей приходится на 2 равные части, или столько было бы тетрадей в двух пачках, если бы их было поровну;
2) 60 : 2 = 30 (т) – столько тетрадей приходится на 1 часть, или столько тетрадей было во второй пачке;
3) 30 + 10 = 40 (т) – столько тетрадей было в первой пачке.
Мы использовали при решении вспомогательную модель – чертеж, которая показывает и второй способ решения. Если за 1 часть принять тетради в первой пачке, то чтобы во второй стало столько же, надо к ней прибавить 10 тетрадей:
Существует и третий арифметический способ решения данной задачи:
1) 10 : 2 = 5(т.) – столько тетрадей надо переложить из первой пачки во вторую, чтобы в них стало поровну;
2) 70 : 2 = 35 (т.) – столько тетрадей в каждой пачке, если из первой переложить во вторую 5 тетрадей;
3) 35 + 5 = 40 (т.) – столько тетрадей в первой пачке;
4) 35 – 5 = 30 (т.) – столько тетрадей во второй пачке.
Ответ: в первой пачке 40 тетрадей, во второй – 30 тетрадей.
Задачи для самостоятельной работы.
Чтобы приготовить овощной салат, на 10 частей картофеля берут 3 части свеклы и 2 части моркови. Сколько картофеля надо взять, если для салата имеется 150 г свеклы?
Спортивная школа получила 120 мячей. Из них 2 части составляли волейбольные мячи, 5 частей футбольные и 3 части баскетбольные. Сколько мячей получила каждая спортивная секция?
Пальто в 6 раз дороже шапки. Сколько стоит шапка, если за всю покупку заплатили 238 рублей?
На пароходе было 240 пассажиров, причем мужчин было в три раза меньше, чем женщин, а детей столько же, сколько мужчин и женщин вместе. Сколько было на пароходе мужчин, женщин и детей в отдельности?
Чтобы приготовить фасолевый салат, на 7 частей фасоли берут 4 части курицы и 2 части сыра. Сколько фасоли надо взять, если для салата имеется 360 г курицы?
Стол в 2 раза дешевле шкафа. Сколько стоит стол, если за всю покупку заплатили354 рубля?
Тесто для вареников содержит 16 частей творога, 3 части муки, 3 части сметаны и 3 части сахара. Найдите массу каждого продукта, необходимого для приготовления 1 кг теста.
Для компота взяли 6 частей яблок, 5 частей груш и 3 части слив. Груш и слив вместе было 2 кг 400 г. Какова была общая масса всех фруктов?
В магазин завезли 540 кг огурцов, помидоров и картофеля, причем помидоров было в два раза больше, чем огурцов, а картофеля столько, сколько помидоров и огурцов вместе. Сколько килограммов овощей каждого вида завезли в магазин?
Для варенья на 2 части малины берут 3 части сахара. Сколько килограммов сахара следует взять на 2 600 г ягод?
Шоколадные конфеты составляют 3 части, карамель – 2 части, ириски – 5 частей всех конфет. За карамель с ирисками заплатили 140 рублей. Сколько заплатили за шоколадные конфеты?
Купили 90 тетрадей в клетку и в линейку, причем тетрадей в клетку взяли 4 части, а в линейку-1 часть. Сколько купили тетрадей в клетку? Сколько купили тетрадей в линейку?
Для варенья на 2 части малины берут 3 части сахара. Сколько килограммов малины было у мамы, если для варки варенья она приготовила 4 500 г сахара?
Шоколадные конфеты составляют 2 части, карамель – 4 части, ириски – 3 частей всех конфет. Определите массу всех конфет, если масса ирисок и карамели – 210 грамм.
В плацкартном вагоне было 3 части спальных мест, и 1 часть спальных мест в мягком вагоне. Всего в плацкартном и мягком вагонах 72 спальных места. Сколько спальных мест в мягком вагоне?
В бочке 40 л. воды. Отлили воды в 3 раза больше, чем осталось. Сколько воды осталось в бочке?
У брата в 2 раза больше марок, чем у сестры, а всего у них 120 марок. Сколько марок у брата?
Альбом в 4 раза дороже тетради, а тетрадь на 21 р. дешевле альбома. Сколько стоит альбом?
Пальто в 6 раз дороже шапки. Сколько стоит шапка, если за всю покупку заплатили 238 рублей?
В бочке 50 л. воды. Отлили воды в 4 раза больше, чем осталось. Сколько воды осталось в бочке?
У сестры в 3 раза больше марок, чем у брата, а всего у них 120 марок. Сколько марок у сестры?
Книга в 10 раз дороже блокнота, а блокнот на 50 р. дешевле книги. Сколько стоит книга?
Стол в 2 раза дешевле шкафа. Сколько стоит стол, если за всю покупку заплатили 354 рубля?
Требуется смешать 3 части песка и 2 части цемента. Сколько цемента и песка
нужно взять отдельно, чтобы получить 30 кг смеси?
Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши
3 части, сливы 2 части общего веса всех фруктов. Сколько граммов яблок,
груш и слив было в отдельности?
Яблоки составляют 7 частей, груши 4 части, сливы 5 частей общего веса
сухофруктов. Найдите общий вес сухофруктов, если в них содержится 160 г груши?
При пайке изделий из жести применяют сплав, содержащий 2 части свинца и 5 частей олова
а) Кусок сплава весит 350 г. Сколько в нем содержится свинца и сколько
олова?
б) Сколько свинца и олова содержит кусок сплава, в котором олова на 360 г больше, чем свинца?
При помоле на каждые 3 части муки получается 1 часть отходов. Сколько
смололи ржи, если муки получилось на 36 ц больше, чем отходов?
Взяли 6 частей яблок, 5 частей груш и 3 части слив. Груш и слив вместе
2 кг 400 г. Сколько всего сухофруктов?
Купили 60 тетрадей, причем тетрадей в клетку было в 2 раза больше, чем
тетрадей в линейку. Сколько частей приходится на тетради в линейку; на
тетради в клетку; на все тетради. Сколько купили тетрадей в клетку,
сколько в линейку?
На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках
вместе – 420 книг. Сколько книг стояло на каждой полке?
За рубашку и галстук папа заплатил 140 руб. Рубашка дороже галстука
в 4 раза. Сколько стоит галстук?
Девочка прочитала в 3 раза меньше страниц, чем ей осталось прочитать.
Всего в книге 176 страниц. Сколько страниц прочитала девочка?
Надо разложить в два пакета 56 орехов так, чтобы в одном было в 3 раза
больше, чем в другом. Сколько орехов надо положить в каждый пакет?
В отрывном календаре 366 листов. К сентябрю в календаре осталось листов в
2 раза меньше, чем оторвали. Сколько листов оторвали?
Ученик купил тетрадей в клетку в 3 раза больше, чем тетрадей в линейку.
Причем их было на 18 больше, чем тетрадей в линейку. Сколько тетрадей
купил ученик?
На первой полке стояло в 4 раза больше книг, чем на второй. Это на 12 книг
больше, чем на второй полке. Сколько книг стояло на каждой полке?
За три дня Митя прочитал 84 страницы. В первый день он прочитал в 3 раза
больше чем во второй, а в третий – 16 страниц. Сколько страниц прочитал
Митя в первый день?
Кусок ткани длиной 76 м разрезали на 3 части. Первая из них имеет длину
25 м, а вторая в 2 раза короче третьей. Найдите длину второй и третьей
части.
Дочка младше мамы в 4 раза и младше бабушки в 9 раз. Сколько лет
каждой, если вместе им 98 лет?
У Сережи в коллекции в 3 раза меньше марок, чем у Васи, а у Андрея
в 2 раза больше, чем у Васи. Сколько марок у каждого, если у Андрея
на 80 марок больше, чем у Сережи?
В двух коробках 36 кусков мела. Когда из одной коробки израсходовали
12 кусков мела, то в ней стало в 3 раза меньше мела, чем в другой. Сколько
кусков мела было в каждой коробке первоначально?
В двух банках 5 л молока. Когда в одну банку добавили 1 л, то в ней стало в 2 раза больше молока, чем в другой. Сколько литров молока было в каждой банке первоначально?
В трех больших пакетах и четырех маленьких содержится 550 г печенья. Сколько граммов в маленьком пакете, если в него входит в 2 раза меньше печенья, чем в большом?
В шести маленьких коробках на 12 карандашей больше, чем в двух больших. Сколько карандашей во всех маленьких коробках и сколько во всех больших, если в одной маленькой коробке в 2 раза меньше карандашей, чем в большой?
Я провел год в деревне, в Москве и в дороге — и притом в Москве в 8 раз более времени, чем в дороге, а в деревне в 8 раз более, чем в Москве. Сколько дней провел я в дороге, в Москве и в деревне?
Календарь дороже общей тетради в 2 раза, а вместе они стоят 9 р . Сколько стоит календарь?
Мальчик и девочка рвали в лесу орехи. Всего они сорвали 120 штук. Девочка сорвала в два раза меньше мальчика. Сколько орехов было у мальчика и девочки в отдельности?
Девочка прочитала в 3 раза меньше страниц, чем ей осталось прочитать. Всего в книге 176 страниц. Сколько страниц прочитала девочка?
Чтобы сварить рисовую кашу, надо взять 4 части крупы и 6 части воды. Сколько потребуется воды, если в кастрюлю положили 160 г крупы?
В сплаве содержится 2 части меди и 1 часть цинка. Сколько меди содержится в 630 г сплава?
Задача 52 взята из повести Н. Носова «Витя Малеев в школе и дома», дающей довольно точное описание характерных ошибок учащихся и самой процедуры поиска решения.
«Прочитал я задачу и даже смех разобрал. «Вот так задача! — думаю. — Чего тут не понимать? Ясно. 120 надо поделить на 2, получится 60. Значит, девочка сорвала 60 орехов. Теперь нужно узнать, сколько мальчик: 120 отнять 60, тоже будет 60. Только как же это так? Получается, что они сорвали поровну, а в задачнике сказано, что девочка сорвала в 2 раза меньше орехов. Ага! — думаю. — Значит, 60 надо поделить на 2, получится 30. Значит, мальчик сорвал 60, а девочка 30 орехов». Посмотрел в ответ; а там: мальчик 80, а девочка 40».
Витя смог решить задачу лишь тогда, когда нарисовал девочку в переднике с одним карманом, а мальчика в курточке с двумя карманами.
«Все 120 орехов теперь лежали у них в трех карманах: в двух карманах у мальчика и в одном кармане у девочки, а всего, значит, в трех. И вдруг у меня в голове, будто молния, блеснула мысль: «Все 120 орехов надо делить на три части!»
Надо сказать, что первое действие, к которому с таким трудом пришел Витя Малеев, вызывает большие трудности у учащихся, этот шаг решения задач «на части» требует специальной отработки, которая будет тем успешнее, чем активнее учащиеся опираются на наглядные образы.
Задачи «на части» в 5-м классе, на ВПР и итоговых экзаменах
Если вы решили заниматься летом с ребёнком математикой, но с трудом вспоминаете школьную программу, наш блогер Александр Шевкин поможет вам всё наверстать. Сегодня он приводит примеры задач «на части» и объясняет, как их решать.
Задачи «на части» являются классическим типом задач, решаемых как арифметически, так и при помощи уравнения. Такие задачи встречаются в учебниках для пятого класса, в ВПР и на выпускном экзамене.
Для развития мышления и речи детей начинать лучше с арифметического способа решения. Рассмотрим решения двух задач из учебника «Математика, 5» (Просвещение, С. М. Никольский и др.) В первых задачах части упоминаются явно.
Задача 1. Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара следует взять на 6 кг ягод?
Решение: По условию задачи ягод 6 кг, и это количество составляет 2 части, поэтому на каждую часть приходится:
Сахара надо взять 3 такие же части, то есть:
В следующей задаче некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.
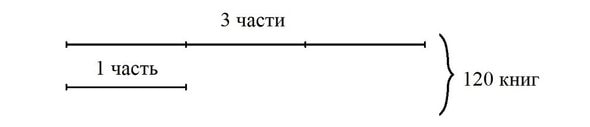
Задача 2. На двух полках стоит 120 книг — на первой полке в 3 раза больше, чем на второй. Сколько книг стоит на каждой полке?
Решение: Если книги, стоящие на второй полке, составляют 1 часть, то на первой полке — 3 такие части. Выполним схематический рисунок.
1) Сколько частей составляют 120 книг?
2) Сколько книг приходится на 1 часть?
3) Сколько книг приходится на первую полку?
Ответ: 90 и 30 книг.
Следующая задача была предложена на экзамене «Математическая грамотность» (Казахстан). Это аналог нашего ЕГЭ базового уровня для выпускников средней школы.
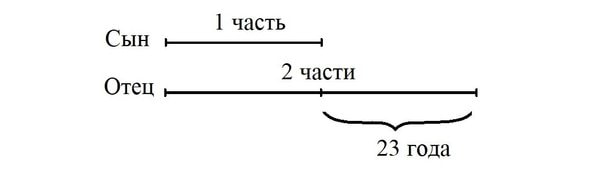
Задача 3. Когда отцу был 31 год, сыну было 8 лет. Сейчас отец в 2 раза старше сына. Сколько лет сыну сейчас?
Решение: Отец старше сына на 31 — 8 = 23 года. Пусть сейчас возраст сына составляет 1 часть, тогда возраст отца — 2 такие же части. Выполним схематический рисунок.
Замечание. Эту задачу преподаватель из ютьюба, обучавший выпускников казахстанских школ, решал при помощи уравнения, приняв за x число лет, прошедших между описанными в задаче событиями.
В заключение задача посложнее.
Задача 4. Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши 3 части, а сливы 2 части общего веса сухофруктов. Сейчас граммов яблок, груш и слив было в отдельности?
1) 4 + 3 + 2 = 9 (частей) — приходится на 1800 г,
2) 1800: 9 = 200 (г) — приходится на 1 часть,
3) 200 ∙ 4 = 800 (г) — было яблок,
4) 200 ∙ 3 = 600 (г) — было груш,
5) 200 ∙ 2 = 400 (г) — было слив.
Ответ: 800, 600 и 400 г.
Отметим, что приём решения задач «на части» может использоваться при решении более сложных составных задач.
Задача 5. На двух полках стояли 36 книг. Когда с первой полки на вторую переставили 3 книги, то книг на второй полке стало в 2 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?
Решение: Пусть количество книг на первой полке после перестановки трёх книг составляет 1 часть, тогда на второй полке — 2 части.
1) 1 + 2 = 3 (части) — приходится на 36 книг,
2) 36: 3 = 12 (книг) — приходится на 1 часть (стало на 1-й полке),
3) 36 — 12 = 24 (книг) — стало на 2-й полке.
Вернём три книги на первую полку.
4) 12 + 3 = 15 (книг) — было на первой полке первоначально,
5) 24 — 3 = 21 (книга) — была на второй полке первоначально.
Ответ: 15 и 21 книга.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.