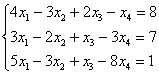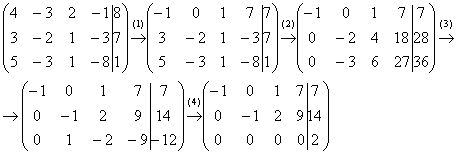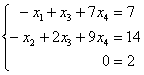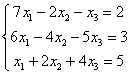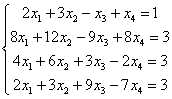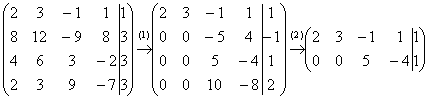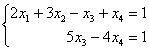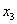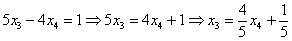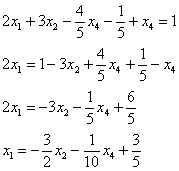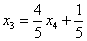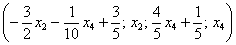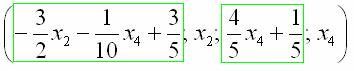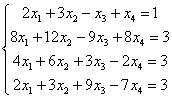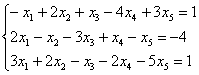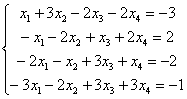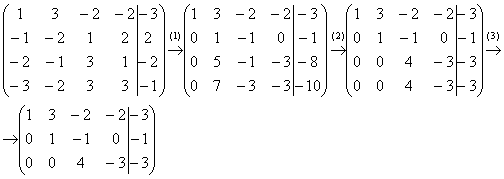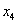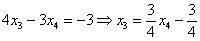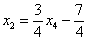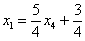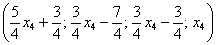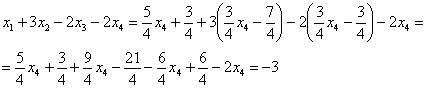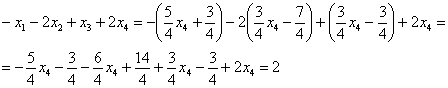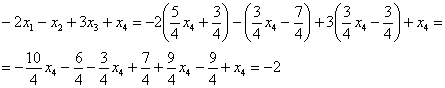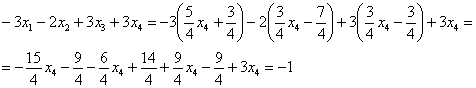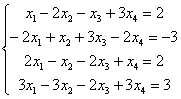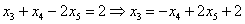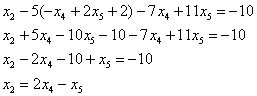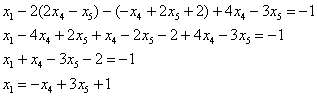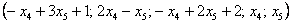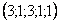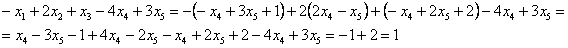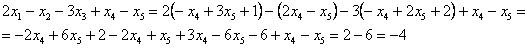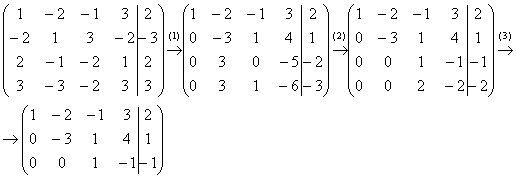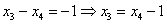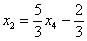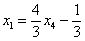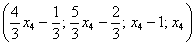Неизвестных больше чем уравнений
Если число неизвестных больше числа уравнений



Тема № 4. Примеры применения методов теории систем и системного анализа для исследования сложных систем и принятия решений.
Модели постепенной формализации задач при организации технологических процессов производства и управления.
Если число неизвестных больше числа уравнений.
Во многих практических ситуациях планирования и управления технологическими процессами сразу не удаётся найти подходящий метод формализованного представления, который позволяет решить задачу, или же, предложив формальную модель, не удается доказать её адекватность отображаемой ситуации.
В этих случаях можно попытаться получить модель или доказать соответствие её реальной действительности путем организации процесса постепенной формализации задачи, позволяющего пошагово уточнять постановку задачи, обосновывать адекватность моделей, и в результате – получать ответы на постановленные в задаче вопросы.
Необходимость в таком подходе может возникнуть в тех случаях, когда, например, после описания ситуации принятия решения в виде системы алгебраических уравнений решение не может быть получено математическим путем (если, например, число неизвестных больше, чем число уравнений), или когда задачу не удаётся описать с помощью моделей математического программирования.
Рассмотрим идею постепенной формализации на примере элементарного эксперимента, который был проведен в 1972 году.
Пятикласснице была предложена задача, которую невозможно было решить известными ей методами математики. Задача, которая была заимствована из раздела головоломок одного из популярных журналов, формулировалась следующим образом.
Известно: в столовую вошла группа посетителей, которые вначале сели за несколько столов по 6 и по 7 человек, а затем разместились поровну, по 11 человек, заняв Z столов. Требуется определить: сколько посетителей вошло в столовую, если известно, что их было больше 100 и меньше 150.
Для отображения этой ситуации легко написать
уравнение 6х + 7у = 11z
и ограничение 100
| х 1 = 6 | 7 х 1 = 7 | 11 х 1 =1 |
| 6 х 2 = 12 | 7 х 2 = 14 | 11 х 2 = 22 |
| 6 х 3 = 18 | 7 х 3 = 21 | 11 х 3 = 33 |
| 6 х 4 = 24 | 7 х 4 = 28 | 11 х 4 = 44 |
| 6 х 5 = 30 | 7 х 5 = 35 | 11 х 5 = 55 |
| 6 х 6 = 36 | 7 х 6 = 42 | 11 х 6 = 66 |
| 6 х 7 = 42 | 7 х 7 = 49 | 11 х 7 = 77 |
 6 х 8 = 48 6 х 8 = 48 | 7 х 8 = 56 | 11 х 8 = 88 |
| 6 х 9 = 54 | 7 х 9 = 63 | 11 х 9 = 99 |
| 6 х 10 = 60 | 7 х 10 = 70 | 11 х 10 = 110 |
| 6 х 11 = 66 | 7 х 11 = 77 | 11 х 11 = 121 |
| 6 х 12 = 72 | 7 х 12 = 84 | 11 х 12 = 132 |
| 6 х 13 = 78 | 7 х 13 = 91 | 11 х 13 = 143 |
| 6 х 14 = 84 | 7 х 14 = 98 | 11 х 14 = 154 |
| 6 х 15 = 90 | 7 х 15 = 105 | 11 х 15 = 165 |
Затем, подождав, пока под членами уравнения появятся числа до умножения на 15, проводившие эксперимент, руководствуясь одним из принципов идеи постоянной формализации и исследования сложных систем – не увлекайся перечислением элементов (в данном случае за элементы приняты 6х, 7у, 11z)– предложили школьнице остановиться и подумать, что можно сделать с полученными столбцами произведений дальше, т. е. предложили возвратиться к формулировке задачи.
Исходное уравнение (1.1) подсказывает, что сумма любого из произведений первого столбца и любого из произведений второго столбца должна дать одно из произведений правой части уравнения. Однако перебор при этом (в рассматриваемой задаче это – число размещений с повторениями) в случае 15 произведений под тремя столбцами составит 15 3 =3375!
Первая подсказка для ограничения перебора содержится в условии задачи, в ограничении 100
Решение систем линейных уравнений. Несовместные системы.
Системы с общим решением. Частные решения
Продолжаем разбираться с системами линейных уравнений. До сих пор я рассматривал системы, которые совместны и имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом, методом Гаусса. Однако на практике широко распространены еще два случая:
– Система несовместна (не имеет решений);
– Система совместна и имеет бесконечно много решений.
Примечание: термин «совместность» подразумевает, что у системы существует хоть какое-то решение. В ряде задач требуется предварительно исследовать систему на совместность, как это сделать – см. статью о ранге матриц.
Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса. На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса для чайников.
Сами элементарные преобразования матрицы – точно такие же, разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).
Решить систему линейных уравнений
Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.
Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.
(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.
(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.
(4) К третьей строке прибавляем вторую строку.
Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: 

Если в результате элементарных преобразований получена строка вида 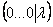
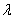
Как записать концовку задания? Нарисуем белым мелом: «в результате элементарных преобразований получена строка вида 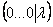
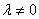
Если же по условию требуется ИССЛЕДОВАТЬ систему на совместность, тогда необходимо оформить решение в более солидном стиле с привлечением понятия ранга матрицы и теоремы Кронекера-Капелли.
Обратите внимание, что здесь нет никакого обратного хода алгоритма Гаусса – решений нет и находить попросту нечего.
Решить систему линейных уравнений
Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Снова напоминаю, что ваш ход решения может отличаться от моего хода решения, у алгоритма Гаусса нет сильной «жёсткости».
Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же, как только появилась строка вида 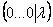
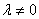

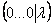
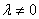
Когда система линейных уравнений не имеет решений – это почти подарок, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия.
Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.
Решить систему линейных уравнений
Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом его и универсальность.
Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Вот и всё, а вы боялись.
(1) Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на –4. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –1.
Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: К четвертой строке прибавляем первую строку, умноженную на –1 – именно так!
(2) Последние три строки пропорциональны, две из них можно удалить.
Здесь опять нужно проявить повышенное внимание, а действительно ли строки пропорциональны? Для перестраховки (особенно, чайнику) не лишним будет вторую строку умножить на –1, а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них.
В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду: 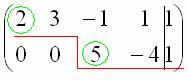
При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.
Перепишем соответствующую систему уравнений:
«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки 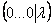
Бесконечное множество решений системы коротко записывают в виде так называемого общего решения системы.
Общее решение системы найдем с помощью обратного хода метода Гаусса.
Сначала нужно определить, какие переменные у нас являются базисными, а какие переменные свободными. Не обязательно заморачиваться терминами линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные.
Базисные переменные всегда «сидят» строго на ступеньках матрицы.
В данном примере базисными переменными являются 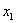
Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: 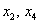
Теперь нужно все базисные переменные выразить только через свободные переменные.
Обратный ход алгоритма Гаусса традиционно работает снизу вверх.
Из второго уравнения системы выражаем базисную переменную 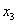
Теперь смотрим на первое уравнение: 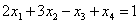
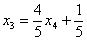
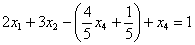
Осталось выразить базисную переменную 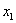
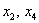
В итоге получилось то, что нужно – все базисные переменные ( 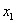
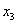
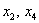
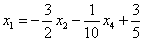
Собственно, общее решение готово:
Как правильно записать общее решение?
Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные 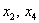
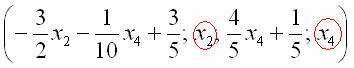
Полученные же выражения для базисных переменных 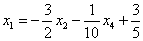
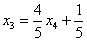
Придавая свободным переменным 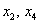
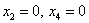
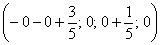
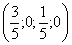
Другой сладкой парочкой являются единицы, подставим 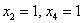
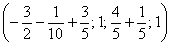
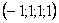
Легко заметить, что система уравнений имеет бесконечно много решений (так как свободным переменным мы можем придать любые значения)
Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение 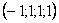
Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.
Но, строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно.
Поэтому более основательна и надёжна проверка общего решения. Как проверить полученное общее решение 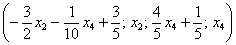
Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае 
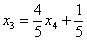
В левую часть первого уравнения системы: 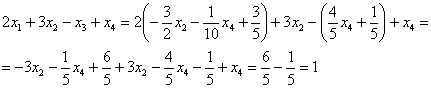
Получена правая часть исходного уравнения.
В левую часть второго уравнения системы: 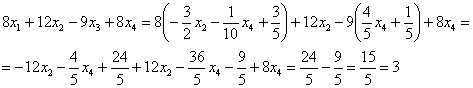
Получена правая часть исходного уравнения.
И далее – в левые части третьего и четвертого уравнение системы. Это дольше, но зато гарантирует стопроцентную правильность общего решения. Кроме того, в некоторых заданиях требуют проверку общего решения.
Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.
Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений. Что важно в самом процессе решения? Внимание, и еще раз внимание. Полное решение и ответ в конце урока.
И еще пара примеров для закрепления материала
Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения
Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2) К третьей строке прибавляем вторую строку, умноженную на –5. К четвертой строке прибавляем вторую строку, умноженную на –7.
(3) Третья и четвертая строки одинаковы, одну из них удаляем.
Вот такая красота: 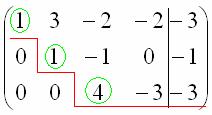
Базисные переменные сидят на ступеньках, поэтому 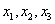
Свободная переменная, которой не досталось ступеньки здесь всего одна:
Обратный ход:
Выразим базисные переменные через свободную переменную:
Из третьего уравнения:
Рассмотрим второе уравнение 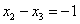
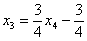
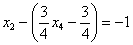
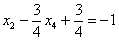
Рассмотрим первое уравнение 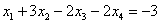
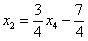
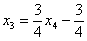
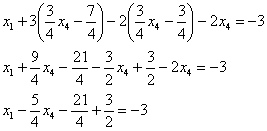
Таким образом, общее решение:
Еще раз, как оно получилось? Свободная переменная 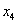
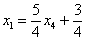
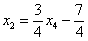
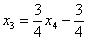
Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =)
Подставляем трех богатырей 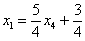
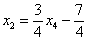
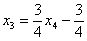
Получены соответствующие правые части уравнений, таким образом, общее решение найдено верно.
Теперь из найденного общего решения 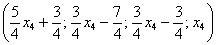
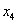
Пусть 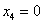
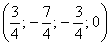
Пусть 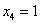
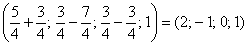
Ответ: Общее решение: 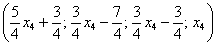
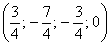
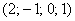
Много математики вредно, поэтому похожий заключительный пример для самостоятельного решения.
Найти общее решение системы линейных уравнений.
Проверка общего решения у меня уже сделана, ответу можно доверять. Ваш ход решения может отличаться от моего хода решения, главное, чтобы совпали общие решения.
Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.
Остановлюсь на некоторых особенностях решения, которые не встретились в прорешанных примерах.
В общее решение системы иногда может входить константа (или константы), например: 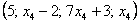
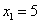
Редко, но встречаются системы, в которых количество уравнений больше количества переменных. Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.
И, конечно, повторюсь в своем совете – чтобы комфортно себя чувствовать при решении системы методом Гаусса, следует набить руку и прорешать хотя бы десяток систем.
Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду. 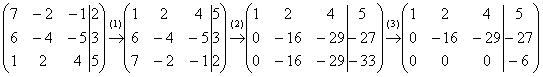
Выполненные элементарные преобразования:
(1) Первую и третью строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –6. К третьей строке прибавили первую строку, умноженную на –7.
(3) К третьей строке прибавили вторую строку, умноженную на –1.
В результате элементарных преобразований получена строка вида 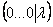

Ответ: решений нет.
Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: 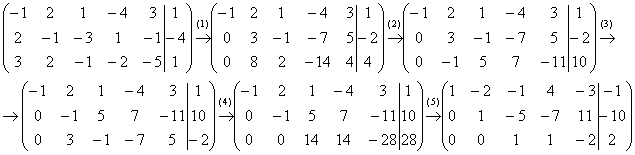
Выполненные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на 2. К третьей строке прибавили первую строку, умноженную на 3.
Для второй ступеньке нет единицы, и преобразование (2) направлено на её получение.
(2) К третьей строке прибавили вторую строку, умноженную на –3.
(3) Вторую с третью строки поменяли местами (переставили полученную –1 на вторую ступеньку)
(4) К третьей строке прибавили вторую строку, умноженную на 3.
(5)У первых двух строк сменили знак (умножили на –1), третью строку разделили на 14.
Обратный ход.
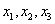
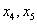
Выразим базисные переменные через свободные переменные:
Из третьего уравнения:
Рассмотрим второе уравнение: 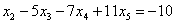
Подставим в него найденное выражение 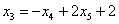
Рассмотрим первое уравнение: 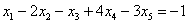
Подставим в него найденные выражения: 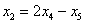
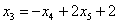
Общее решение:
Найдем два частных решения
Если 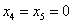
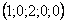
Если 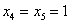
Ответ: Общее решение: 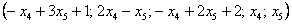
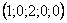
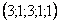
Проверка: подставим найденное решение (выражения базисных переменных 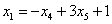
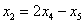
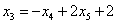
Получены соответствующие правые части, таким образом, общее решение найдено верно.
Пример 6: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) Ко второй строке прибавляем первую строку, умноженную на 2. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –3.
(2) К третьей строке прибавляем вторую строку. К четвертой строке прибавляем вторую строку.
(3) Третья и четвертая строки пропорциональны, одну из них удаляем.
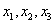
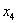
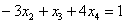
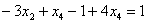
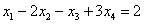

Ответ: Общее решение:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5