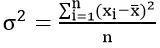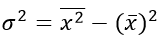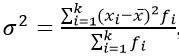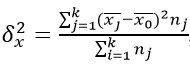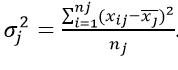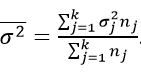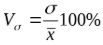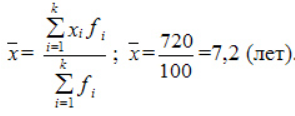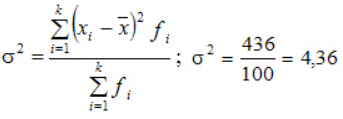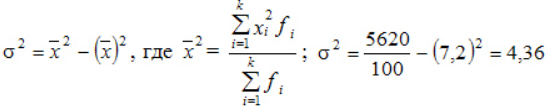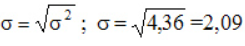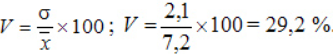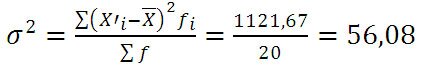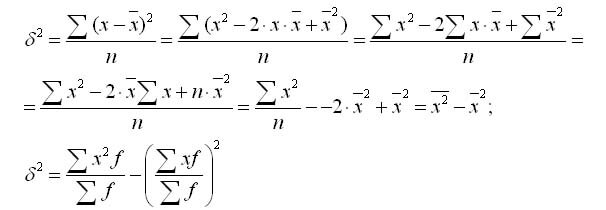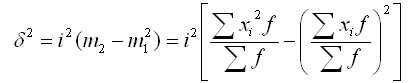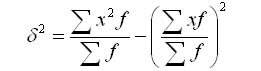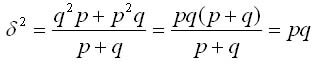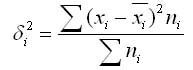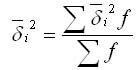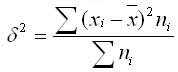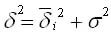Небольшая дисперсия числового набора показывает что исследуемая величина

Дисперсия свойства, формула вычисления дисперсии дискретной случайной величины, виды, правило и примеры расчетов, онлайн-калькулятор

В различных научных дисциплинах словосочетание «дисперсия это» характеризует мало схожие понятия. С латыни «dispersio» переводится как «рассеяние».

В физике, например, означает связь фазовой скорости волны с частотой. В химии описывает несмешиваемые субстанции. В биологии – многообразие признаков популяции.

В данной статье речь пойдет о математической трактовке. Рассматривается как одно из свойств случайных величин.

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где xi – значение из ряда;

fi – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

nj – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

Пример расчета дисперсии

Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

Методическая разработка урока по теории вероятностей. Тема урока: «Числовые характеристики случайных величин»

Разделы: Математика

Тема урока: «Числовые характеристики случайных величин».

Используемые средства обучения: ПК, проектор.

Ожидаемые результаты.

I. Организационный момент

Сообщить тему и цели урока.

II. Актуализация знаний учащихся

Вопросы фронтального опроса:

– Hазовите виды случайных величин.
– Hазовите закон распределения вероятностей дискретной случайной величины.

III. Изучение нового материала, формирование знаний, умений и навыков

Рассмотрим эти характеристики для дискретной случайной величины.

Математическое ожидание

Пример 1. Закон распределения вероятностей дискретной случайной величины дан в виде таблицы. Найти математическое ожидание этой величины.

Пример 2. На рынке куплены одинаковые по размеру лимоны:

3 лимона – по 20 руб за штуку,
12 лимонов – по 10 руб за штуку. Найти математическое ожидание стоимости одного лимона.

руб.

Пример 3. Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем 500 рублей, 10 билетов по 100 руб и остальные по 5 рублей (беспроигрышная лотерея). Наудачу выбирают билет. Найти математическое ожидание выигрыша.

Для того, чтобы лотерея приносила доход, цена билета должна быть больше, чем средний выигрыш, например 30 руб (Доход 3000 – 1945 = 1055 руб).
Отдельный игрок может и выиграть, но в конечном итоге доход будет у организатора лотереи.

Свойства математического ожидания

Доказательство 2-го свойства

Пример.

Производится 3 выстрела с вероятностями p₁ = 0,4; p₂ = 0,3; p₃ = 0,6. Найти математическое ожидание общего числа попаданий, если:

Пример. Найти математическое ожидание случайной величины (4Х + 5) если М(Х) = 2.

Дисперсия

Случайные величины могут иметь одинаковые математические ожидания, но различные возможные значения.

Математические ожидания равны.

Возможные значения Y близки к M(Y) возможные значения Х далеки от своего M(X) то есть для характеристики случайной величины математического ожидания недостаточно, нужна характеристика рассеивания, т.е. разброса значений случайной величины, например в артиллерии важно насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.

Наиболее полной характеристикой разброса чисел является набор их отклонений от математического ожидания. Но когда набор чисел велик, рассматривать набор отклонений практически неудобно. Нужно описать разнообразие чисел в наборе одной характеристикой, одним числом.

Размах – слишком грубая мера разброса чисел в наборе, поскольку учитывает только два из них – наименьшее и наибольшее. Можно попробовать взять «среднее отклонение».

Для любого набора, если только не все числа в нем равны, часть отклонений будет положительна, а часть отрицательна. При этом сумма отклонений равна 0.

В этом состоит основное свойство отклонений: сумма отклонений чисел от математического ожидания этих чисел равна нулю.

Сумма отклонений всегда равна нулю, поэтому среднее арифметическое отклонений тоже равна нулю и его нельзя использовать как меру разброса.

Дисперсия – это среднее арифметическое квадратов разностей между значениями случайной величины и ее средним значением. В наших обозначениях:

Или в общем виде дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее среднего значения.

Метод сравнения средних значений и дисперсий используется в самых разных отраслях человеческой деятельности. В медицине – для установления диагноза, в литературоведении – для определения автора произведения (когда авторство является спорным), в криминалистике – для розыска преступников.

Пример. Органами милиции задержан грузовик с помидорами, похищенными на овощной базе. В городе всего четыре базы, каждая из них получает помидоры из своего сельскохозяйственного района. Определите, с какой базы были вывезены помидоры. Расследование осложняется тем, что помидоры на всех базах одного сорта.

Решение.

Воспользуемся методом сравнения средних значений и дисперсий. В каждом сельскохозяйственном районе свои условия произрастания помидоров, поэтому помидоры разных районов отличаются, скажем, удельным весом (диаметром, весом и др.). Выберем по 20 – 25 помидоров (реально, конечно, больше) на каждой овощной базе и из грузовика. У нас получатся 4 последовательности – по одной для каждой базы, и еще одна – для грузовика, с которого мы и будем сравнивать первые четыре. Это наши исходные данные. Результатом является номер овощной базы, где совершено хищение.

Чтобы добиться этого результата, нужно, как рассказано выше, вычислить средние значения и дисперсии всех пяти последовательностей и провести сравнение.

Пусть вес 1 помидора на соответствующих базах и в грузовике изменяется в пределах (в г):

1-я (70, 100)
2-я (80, 90)
3-я (75, 95)
4-я (90, 120
Грузовик (80, 90).

Сравнивая, замечаем, что дисперсии и средние одновременно близки у грузовика и второй базы. Значит, помидоры украдены со второй базы.

Пример. Найти дисперсию случайной величины Х

M(X) = 1 . 0,3 + 2 . 0,5 + 5 . 0,2 = 0,3 + 1,0 + 1,0 = 2,3
(x₁ – M(X)) 2 = (1 – 2,3) 2 = ( – 1,3) 2 = 1,69
(x₂ – M(X)) 2 = (2 – 2,3) 2 = 0,09
(x₃ – M(X)) 2 = (5 – 2,3) 2 = 7,29

Напишем закон распределения квадрата отклонения:

D(X) = 1,69 . 0,3 + 0,09 . 0,5 + 7,29 . 0,2 = 2,01

Вычисления громоздки, есть формула, позволяющая быстрее вычислить значение дисперсии.

Формула для вычисления дисперсии

Пример.

M(X) = 2 . 0,1 + 3 . 0,6 + 5 . 0,3 = 0,3 + 1,0 + 1,0 = 3,5.

M(X 2 ) = 4 . 0,1 + 9 . 0,6 + 25 . 0,3 = 0,3 + 1,0 + 1,0 = 13,3

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю D(C) = 0

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D(CX) = C 2 D(X)

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин D(X + Y) = D(X) + D(Y)

4. Дисперсия разности двух независимых величин равна сумме их дисперсий D(X – Y) = D(X) + D(Y)

Следствия

Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых р – вероятность появления постоянна: D(X) = n . p . q.

Пример. Производится 10 независимых испытаний р = 0,6.

D(X) = n . p . q = 10 . 0,6 . 0,4 = 2,4

Среднее квадратическое отклонение

Дисперсия имеет размерность равную квадрату размерности случайной величины. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют не дисперсию, а среднее квадратическое отклонение:

Среднее квадратическое отклонение равно корню квадратному из дисперсии, поэтому его размерность равна размерности случайной величины. Например, если Х выражается в линейных метрах, то тоже выражается в линейных метрах, а D(X) – в квадратных метрах.

Подведение итогов

На уроке мы рассмотрели числовые характеристики случайных величин, способы их вычисления, свойства.

Задача 1. Дано распределение случайной величины Z

Вычислить дисперсию этой случайной величины.

Задача 2. Дисперсия случайной величины Х равна 3. Найдите D(Y), где

а) Y = 3X:
б) Y = X + 5;
в) y – 4X;
г) Y = 2X – 1;
д) Y = 5 – 3X;
е) Y = – 5X – 7.

Источник

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

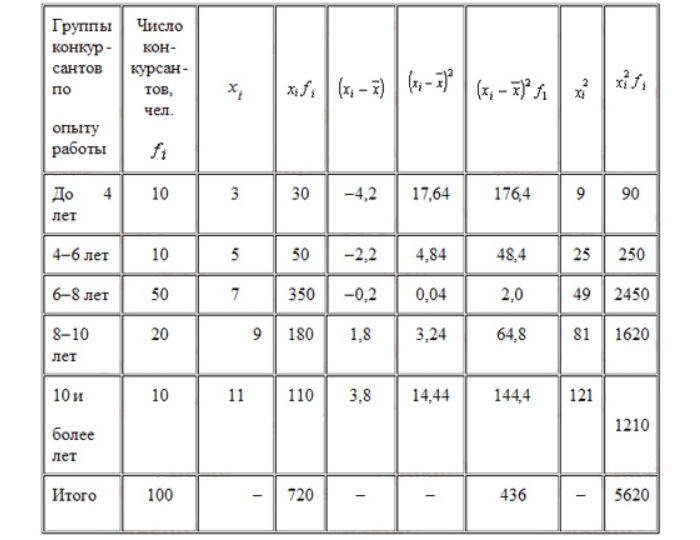
Пример расчета дисперсии

Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

Дисперсия, виды и свойства дисперсии

Понятие дисперсии

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

где n — частота (повторяемость фактора Х)

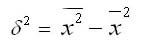
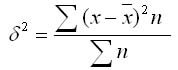
Пример нахождения дисперсии

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

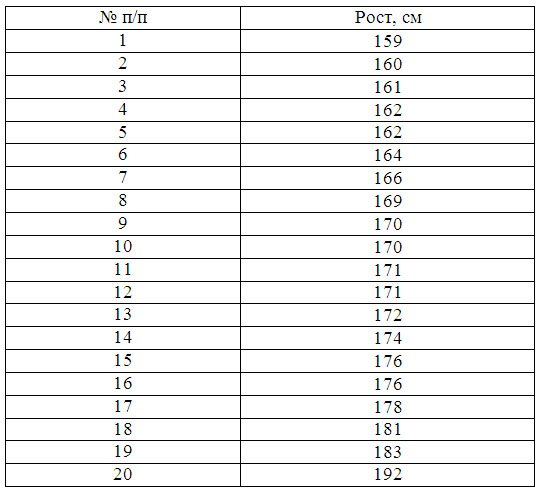
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:

Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

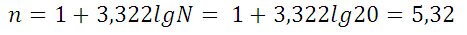
Составим интервальную группировку

Для дальнейших расчетов построим вспомогательную таблицу:

X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

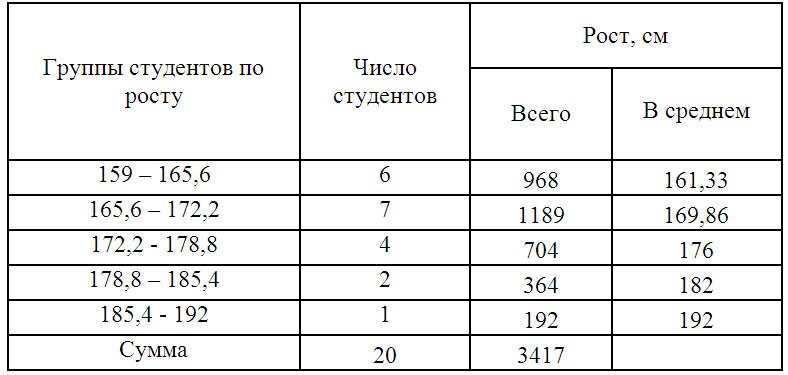
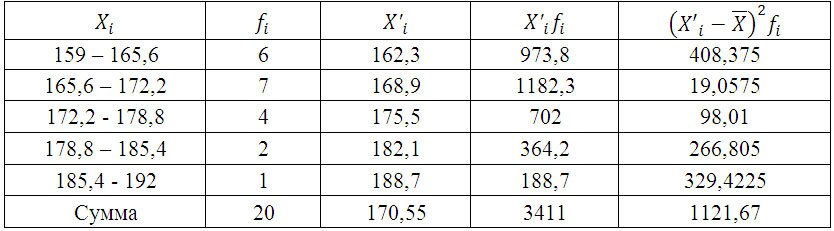
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

Определим дисперсию по формуле:

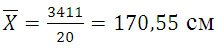
Формулу дисперсии можно преобразовать так:

Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:

где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

где хi — групповая средняя;
ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

Правило сложения дисперсии в статистике

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

Свойства дисперсии

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Источник