Объемные фигуры что это

Геометрические фигуры плоские и объёмные

Цели урока:

Планируемые результаты:

личностные:

метапредметные:

предметные:

УУД общенаучные:

УУД личностные:

Тип урока: изучение нового материала.

Методы: словесные, исследовательские, наглядные, практические.

Формы работы: фронтальная, групповая, парная, индивидуальная.

1. Организация начала урока.

Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!

2. Актуализация знаний.

Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!

Чтобы дойти до цели, надо прежде всего идти.

Перед вами высказывание, прочитайте. Что означает это высказывание?

(Чтобы чего-то добиться, нужно что-то делать)

— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.

— Начнем наш путь к достижению цели сегодняшнего урока.

3. Подготовительная работа.

— Посмотрите на экран. Что вы видите? (Геометрические фигуры)

Назовите эти фигуры.

— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)

— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.

— По какому признаку вы разделили эти фигуры?

— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?

— Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)

— Чему мы должны научиться на уроке?

4. «Открытие» нового знания в практической исследовательской работе.

(Учитель показывает куб и квадрат.)

— Можно ли сказать, что это одно и тоже?

— Чем же отличается куб от квадрата?

— Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)

— Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?

! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)

— Можно ли куб полностью (весь) прижать к парте? Проверим.

— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?

! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)

ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)

Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.

4. Открытие новых знаний.

1. Назовите фигуры, изображенные на рисунке.

— Какую форму имеют основания этих фигур?

— Какие еще формы можно увидеть на поверхности куба и призмы?

2. Фигуры и линии на поверхности объемных фигур имеют свои названия.

— Предложите свои названия.

— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.

— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.

Работа с тетрадями: чтение нового материала

Соотнесение реальных объектов и объёмных тел.

— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.

5. Физминутка.

1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.

(Ученики «обхватывают» руками и гладят воображаемый шар.)

А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.

Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.

Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!

6. Групповая работа:

(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1. (Для изучения параллелепипеда)

Группа 2. (Для изучения пирамиды)

Группа 3. (Для изучения куба)

Далее каждая группа выступает, представляя свою объемную фигуру другим.

7. Решение кроссворда

8. Итог урока. Рефлексия деятельности.

Решение кроссворда в презентации

— Что нового вы для себя сегодня открыли?

+ Все геометрические фигуры можно разделить на объёмные и плоские.

Источник

Описание презентации по отдельным слайдам:

Объёмные фигуры. Почему их так называют? Составила: Абрамова А.В. 2020г.

Давайте познакомимся: Куб Призмы Цилиндр Шар Конус Пирамида Параллелепипед «Кликаете» по пустому месту на слайде – появляется фигура и название.

ПАРАЛЛЕЛЕПИПЕД Термин образован путем соединения двух греческих слов: «параллелос» — «параллельный» и «эпипедос» — «плоскость». Параллелепипед — призма, основанием котopoй является параллелограмм.

ЦИЛИНДР Цилиндр – от латинского слова «цилиндрус» (валик, каток).

Термин «шар» происходит от греческого слова «сфайра» в переводе означающего – «мяч». ШАР

ПРИЗМА Термин «призма» происходит от греческого слова «prisma» в переводе означающего – «отпиленный кусочек».

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Воспитание детей дошкольного возраста

Курс повышения квалификации

Деятельность классного руководителя по реализации программы воспитания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1582604

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%

Время чтения: 2 минуты

Большинство родителей в России удовлетворены качеством образования в детсадах

Время чтения: 2 минуты

Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Конспект занятия по ФЭМП «Объемные геометрические фигуры» в подготовительной к школе группе

Айлана Хеймер-ооловна Иргит
Конспект занятия по ФЭМП «Объемные геометрические фигуры» в подготовительной к школе группе

Конспект по ФЭМП: «Объемные геометрические фигуры» в подготовительной к школе группе.

Цель: систематизировать и закрепить математические представления детей подготовительной группы

— закреплять знания геометрических фигур, их элементов (углы, стороны);

— развивать умение группировать геометрические фигуры по цвету и форме;

— упражнять в составлении тематических композиций из геометрических фигур;

— закреплять знания объемных (куб, цилиндр, шар, конус, тор, параллелепипед, призма) и плоскостных (квадрат, треугольник, трапеция, круг, прямоугольник, овал, многоугольник) фигур.

— развивать психологические процессы: слуховое и зрительное внимание, логическое мышление, мелкую моторику рук, воображение, сообразительность;

— развивать социальные навыки: умение работать индивидуально и в коллективе, договариваться, учитывать мнение партнёра;

— развивать умения анализировать предметы сложной формы, составленных из гео-метрических фигур, и воссоздавать модель по образцу;

— развивать у детей логическое мышление, сообразительность, внимание, умение находить признаки сходства и различия.

— воспитывать личностные качества у каждого ребёнка: любознательность, целе-устремлённость, устойчивость интереса к знаниям и умениям, самостоятельность.

Материал: набор геометрических фигур разного цвета, счётные палочки, пласти-лин, набор плоскостных и объёмных фигур, мешочек с фигурами, раздаточный материал «Найди лишнюю фигуру», плакаты плоскостных и объёмных фигур.

Ход занятия.

1. Вступление. Организационный момент.

Воспитатель: Здравствуйте, ребята!

Наши умные головки

Будут думать много, ловко

Ушки будут слушать,

Ротик четко говорить,

Ножки будут топать,

Друг другу улыбаемся,

Занятие начинается.

Воспитатель: Молодцы, ребята! Сегодня на занятии мы с вами вспомним всё, что мы знаем о геометрических фигурах и узнаем новые секреты фигур. Но для того, чтобы вы быстро и правильно отвечали, надо сделать зарядку для ума. Повторение фигур (за-ранее вывешивается плакат геометрическими фигурами разной формы и разных цветов)

Воспитатель: Молодцы! Вот теперь можно приступать к более сложной работе.

— Ребята, у вас на столах у каждого есть набор геометрических фигур. Давайте по-строим дом из фигур. Ставим стену, берем квадрат. Ребята у вас получается? (ответы детей)

Воспитатель: На самом деле. Может прямоугольник может устоять? Может быть круг? Треугольник? Овал? (ответы детей)

Воспитатель: В чём же дело? Какой он тоненький. Ах, да у него же нету тела.

У меня есть тело, и у вас есть тело, можете даже постоять? (ребята встают)

На самом деле мы не падаем. Таким образом мы подводим ребят к понятию «тело».

2. Постановка цели. Геометрическое тело.

Воспитатель показывает фигуры:

Круг –шар (шар стоит, круг нет)

Квадрат – куб (у куба есть тело, а у квадрата нет). А давайте посчитаем стороны куба. Считаем с детьми.

Призма – треугольник. И катится призма не очень.

— Ребята, как называются фигуры, которые изображены на рисунке, давайте пере-числим, начиная с первой.

— Что лежит в основании цилиндра?

— Что лежит в основании конуса?

— Что лежит в основании призмы?

— Что лежит в основании куба? Прямоугольного параллелепипеда?

— А теперь вспомним, что такое грани и назовем количество граней этих фигур. (Показываю грани и считаю их вместе с детьми, демонстрируя это на объемных фигурах)

— Сколько граней у куба? Призмы? Параллелепипеда?

3. Совместная деятельность воспитателя с детьми.

Работа со счётными палочками.

Цель: развивать мелкую моторику рук, воображение, умение, воссоздавать модель по образцу;

Воспитатель: Теперь поработаем со счетными палочками.

Вам будет следующее задание: предлагается детям собрать модель куба при помощи счетных палочек и пластилина. Показываю поэтапно, как собрать куб, параллелепипед, и призму.

Если дети затрудняются, то подсказать им, или помочь выполнить задание.

4. Физминутка «Колобок»

5. Игра «Найди лишнюю фигуру».

Цель: Учить детей находить лишнюю фигуру, ориентируясь на форму (цвет и размер) фигуру, развивать смекалку, сообразительность и логическое мышление

Воспитатель: Ребята посмотрите на картинку, как вы думаете, какая из этих фигур лишняя и по какому принципу? (по цвету, форме, размеру?

7. Игра «Волшебный мешочек»

Цель: закреплять знания геометрических тел.

Воспитатель: Ребята сейчас я вам расскажу сказку.

8. Игра «Геометрический город»

Цель: закрепить знания геометрических тел, развитие мелкой моторики

Воспитатель: Теперь ребята, я, вам предлагаю из объемных геометрических фигур построить город.

Воспитатель: Ребята, вам понравилось моделировать фигуры из счетных палочек? В следующий раз мы попробуем смоделировать другую фигуру.

— Что мы сегодня с вами повторяли? (ответы детей).

— Молодцы, вы хорошо сегодня поработали!

Конспект НОД по ФЭМП в подготовительной к школе группе «Умная мастерская» Интеграция образовательных областей: «Познавательное развитие», Социально-коммуникативное развитие», «Речевое развитие», «Физическое.

Конспект НОД по ФЭМП в подготовительной к школе группе «Умная мастерская» Интеграция образовательных областей: «Познавательное развитие», «Социально-коммуникативное», «Речевое развитие», «Физическое развитие».

Конспект открытого занятия по ФЭМП в подготовительной к школе групп «Занимательная математика» Программное содержание: Цель: закрепление знаний о математических представлениях посредством игры – путешествия. Обучающие задачи: 1. Закрепить.

Конспект занятия по ФЭМП в младшей группе «Геометрические фигуры» Конспект занятия по ФЭМП в младшей группе «Геометрические фигуры» Цель: Совершенствовать умение различать и называть геометрические фигуры:.

Мастер-класс «Объемные фигуры из спичек и пластилина» для детей подготовительной группы Чтобы научить детей делать сложные объемные фигуры, начинаем с проведения занятия, на котором учим изготавливать кубы из спичек и пластилина:.

«Геометрические фигуры. Круг, квадрат». Конспект занятия по математике в младшей группе Программное содержание: 1. Учить сравнивать два предмета по форме и величине. 2. Содействовать овладению умения обследовать геометрические.

Конспект занятия с использованием дидактической игры «Поможем Маше и Мишке выучить основные цвета и геометрические фигуры» Мультимедийная игра «Поможем Маше и Мишке выучить основные цвета и геометрические фигуры» Автор: Белашова Татьяна Анатольевна МДАНОУ детский.

Конспект НОД по ФЭМП в подготовительной к школе группе «Как помочь Буратино» Программное содержание: 1. Закрепить знание детей о последовательности дней недели, о временах года, осенних месяцах; 2. Продолжать учить.

Источник

МНОГОГРАННИКИ (объемные геометрические фигуры): определения, формулы

Призма

Формулы для призмы :

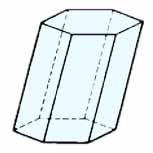
Объем призмы: V = S_o∙h
Площадь поверхности: S = 2∙S_o + S_бок
Где: V — объем призмы, S_o — площадь основания, h – высота, S_бок — площади всех боковых граней.

Параллелепипед

Параллелепипед — это призма, основание которой — параллелограмм.

Формулы для параллелепипеда :

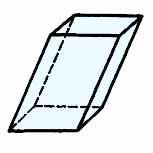
Объем параллелепипеда: V = S_o∙h
Площадь поверхности: S = 2∙S_o + S_бок
Где: V — объем параллелепипеда, S_o — площадь основания, h – высота, S_бок — площади всех боковых граней.

Формулы для прямоугольного параллелепипеда :

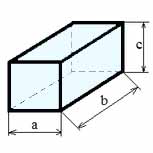
Объем прямоугольного параллелепипеда: V = a∙b∙c = S_o∙ c
Площадь поверхности прямоугольного параллелепипеда:
S = 2·(S_a+S_b+S_c) или S= 2· (a·b+ b·c+ a·c)
Диагональ: d =√(a 2 +b 2 +c 2 )
Где: V — объем прямоугольного параллелепипеда, a — длина, b — ширина, с – высота, So — площадь основания, S_a,S_b,S_c — площади соответствующих сторон.

Формулы для куба :

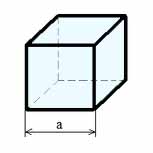
Объем куба: V = a 3
Площадь поверхности куба: S = 6·a 2
Диагональ: d = a√3
Где: V — объем куба, a — длина грани куба.

Пирамида

Формулы для правильной пирамиды :

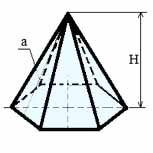
Объем правильной пирамиды: V = 1/3 · (S_o · h)
Площадь боковой поверхности правильной пирамиды: S_бок = ½ · P_о· a
Где: V — объем пирамиды, S_o — площадь основания пирамиды, S_бок — площадь боковой поверхности, P_о — периметр основания правильной пирамиды, h — высота пирамиды. a — апофема правильной пирамиды.

Формулы для правильной треугольной пирамиды :

Объем правильной треугольной пирамиды: V = h·a 2 / (4/√3)
Где: a — сторона правильного треугольника — основания правильной треугольной пирамиды, h — высота правильной треугольной пирамиды

Формулы для правильной четырехугольной пирамиды :

Объем правильной четырехугольной пирамиды: V = 1/3 · h · a 2
Где: a — сторона квадрата — основания правильной четырехугольной пирамиды, h — высота правильной четырехугольной пирамиды.

Формулы для тетраэдра :

Объем тетраэдра: V = (√2 / 12) · a 3
Где: V — объем тетраэдра, a — длина ребра тетраэдра.

Усеченная пирамида

Формулы для усеченной пирамиды :

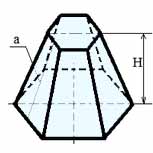
Объем усеченной пирамиды равен разности двух полных пирамид.
Объем правильной усеченной пирамиды:
V = 1/3 · h · (S_осн1 + S_осн2 + √(S_осн1S_осн2))
Боковая поверхность правильной усеченной пирамиды:
S_бок = ½ (P_осн1 + P_осн2) · a
Где: S_осн1, S_осн2 — площади верхнего и нижнего основания усеченной пирамиды, h — высота усеченной пирамиды, P_осн1, P_осн2 — периметры верхнего и нижнего оснований правильной усеченной пирамиды, a — апофема правильной усеченной пирамиды.

Источник

Объемные фигуры что это

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке познакомимся с понятием «объемные тела», а также изучим элементы объемных тел.

Треугольники, квадраты, ромбы, круги, окружности, кубы. Если посмотреть вокруг, то в привычных нам предметах и вещах можно увидеть геометрические фигуры и тела.

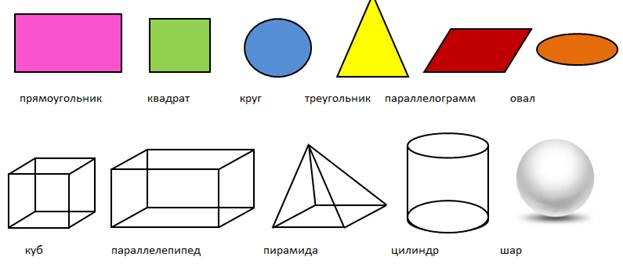
Рассмотрим геометрические фигуры, изображенные на рисунке, и попробуем назвать их.

Фигуры в верхнем ряду нам знакомы, и назвать их не составит труда: прямоугольник, квадрат, круг, треугольник, параллелограмм, овал. Все эти фигуры плоские.

Посмотрим внимательно на фигуры нижнего ряда, там расположены следующие фигуры: куб, параллелепипед, пирамида, цилиндр, шар. Все эти фигуры объемные.

С объемными фигурами мы часто сталкиваемся в обычной жизни.

На какие объемные геометрические фигуры похожи разные предметы?

Автобус формой похож на параллелепипед;

Мячик имеет форму шара;

Банка сгущенки – это цилиндр;

Египетская пирамида – пирамида;

Детские кубики – куб.

Интересно, а в чем отличие объемных геометрических фигур от плоских?

Чтобы ответить на этот вопрос, рассмотрим следующие пары: квадрат и куб, треугольник и пирамида.

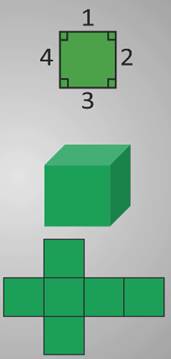
Рассмотрим первую пару: квадрат и куб.

Квадрат – это плоская геометрическая фигура, у которой 4 одинаковые стороны и 4 угла. У квадрата мы можем измерить длину и ширину.

Куб – это объемная фигура.

Если мы развернем куб, то увидим, что он состоит из 6 квадратов.

Значит, квадрат – это элемент куба, его сторона.

У куба мы можем измерить не только длину и ширину, но и высоту.

Рассмотрим вторую пару: треугольник и пирамида.

Треугольник – это плоская геометрическая фигура, у которой 3 стороны и 3 угла.

У треугольника мы можем измерить длины его сторон.

Пирамида – это объемная геометрическая фигура.

Если мы развернем пирамиду, то увидим, что она состоит из 4 треугольников и одного квадрата.

Значит, треугольники и квадрат – это элементы пирамиды, треугольники – это стороны пирамиды, а квадрат – ее основание.

У пирамиды мы можем измерить длину, ширину и высоту.

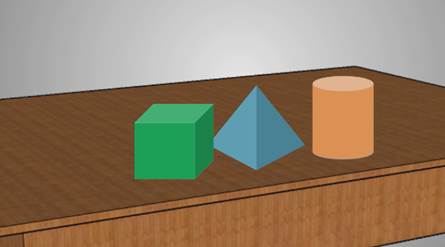
На стол поставим объемные фигуры: куб, пирамиду и цилиндр.

С левой стороны включим настольную лампу.

Объемные фигуры отбрасывают тень.

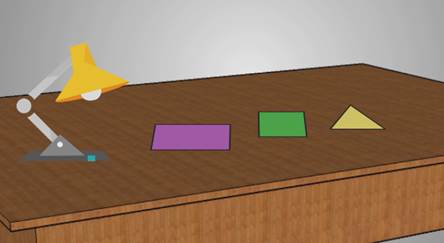
А теперь на стол положим плоские фигуры: квадрат, прямоугольник и треугольник. Включим лампу.

Что заметим на этот раз?

Плоские фигуры не отбрасывают тень, они полностью соприкасаются с поверхностью стола.

Сравнив пары фигур и проведя эксперимент, можем сделать вывод: объемные фигуры отбрасывают тень; у объемных фигур в отличие от плоских имеется три меры: длина, ширина и высота; плоские фигуры являются элементами объемных фигур.

Подведем итоги урока:

1.Все геометрические фигуры в математике можно разделить на две группы: плоские и объемные.

2.Объемные геометрические фигуры – это фигуры, у которых можно измерить длину, ширину и высоту.

3.Объемные фигуры на свету отбрасывают тень.

4.Плоские фигуры являются элементами объемных фигур.

Источник